Nombre narcissique

Exemples de nombres narcissiques.

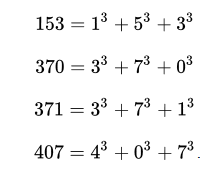
Un nombre narcissique (ou nombre d'Armstrong de première espèce, ou — en anglais — PPDI, pour Modèle:Lang) est un entier naturel $n$ non nul qui est égal à la somme des puissances $p$-ièmes de ses chiffres en base dix, où $p$ désigne le nombre de chiffres de $n$ :

$n=\sum _{k=0}^{p-1}{x}_{k}10^k=\sum _{k=0}^{p-1}(x_k{)}^p\text{avec}{x}_k\in \{0,\dots ,9\}\text{et}{x}_{p-1}\ne 0.$

Exemples

• Tous les entiers de 1 à 9 sont narcissiques.
• Les dix termes suivants de la suite des 88 nombres narcissiques (Modèle:OEIS) sont 153, 370, 371, 407, 1 634, 8 208, 9 474, 54 748, 92 727 et 93 084.
  • $153=1^3+5^3+3^3$.
  • $93084=9^5+3^5+0^5+8^5+4^5$.
• Pour toute base $b⩾2$ entière, l'ensemble des nombres narcissiques dans cette base est fini.

• Le plus grand est 115132219018763992565095597973971522401.

Historique

Dans son livre "536 puzzles and curious problems" , Henri Dudeney (1857 - 1930) pose le problème de trouver des nombres égaux à la somme des cubes de leurs chiffres autres que 407 et 370 (pb 143) .

Variantes des nombres d'Armstrong

• Un nombre d'Armstrong de quatrième espèce, ou Modèle:Lang (PDI) est un entier n qui est égal à la somme des puissances q-ièmes de ses chiffres, mais cette fois pour un entier q > 0 quelconque, non nécessairement égal au nombre p de chiffres de n (un tel n n'est donc généralement pas un nombre narcissique) :Modèle:RetraitIntuitivement, il est clair que si p est le nombre exact de chiffres de n et augmente, q tend à augmenter.

• Pour les nombres d'Armstrong de troisième espèce (PDDI), voir l'article Nombre de Münchhausen.
• Un nombre d'Armstrong n de deuxième espèce vérifie quant à lui :

$n=\sum _{k=0}^{p-1}{x}_{k}10^k=\sum _{k=0}^{p-1}(x_k{)}^{k+1}\text{avec}{x}_k\in \{0,\dots ,9\}$.

• On peut également considérer les nombres d'Armstrong dans une base autre que dix.
• Les nombres égaux à une puissance de la somme de leurs chiffres sont les nombres généralisés de Dudeney.