Surface implicite
Une surface implicite est la surface de niveau d'une fonction différentiable f définie sur un ouvert de .
Exemples
- L'exemple le plus élémentaire est sans nul doute l'exemple des plans affines. Si l est une forme linéaire sur , alors est une application différentiable et tout réel est une valeur régulière de l. Pour r donné, est une surface implicite de .
- Autre exemple élémentaire, si est une forme quadratique non dégénérée de , alors toute valeur non nulle est une valeur régulière de q :
- Si q est définie positive, alors pour , la surface implicite est vide ; et pour , est une sphère.
- Si q est non définie, de signature , la surface implicite est un hyperboloïde à une ou deux nappes suivant le signe de r.
- La trompette de Gabriel est définie par la relation implicite :
- avec a non nul.
La trompette de Gabriel est une surface de révolution.
Illustrations
-
Surface implicite d'un tore (R=40, a=15)
-
Surface implicite de genre 2
-
Surface implicite non algébrique (wineglas)
-
equipotential surface of 4 point charges
-
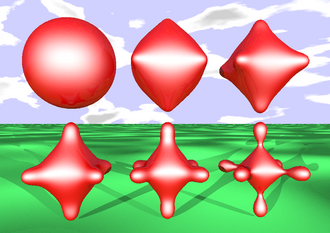
metamorphoses between two implicit surfaces (torus and a constant distance product surface)
-
approximation of three tori (parallel projection)
-
Image PovRay (central projection) of an approximation of three tori
-
Image PovRay : metamorphoses between a sphere and a constant distance product surface (6 points)