Carré parfait

Les trois premiers carrés parfaits non nuls.

En mathématiques, un carré parfait (ou nombre carré s'il est non nul, voire simplement carré s'il n'y a pas ambiguïté) est le carré d'un entier. Dans le système de numération décimal, le chiffre des unités d'un carré parfait ne peut être que [[Zéro|Modèle:Math]], [[1 (nombre)|Modèle:Math]], [[4 (nombre)|Modèle:Math]], [[5 (nombre)|Modèle:Math]], [[6 (nombre)|Modèle:Math]], ou [[9 (nombre)|Modèle:Math]].

Définition et liste

Un carré parfait est le carré d'un entier naturel.

Un nombre carré est un nombre polygonal (donc entier strictement positif) qui peut être représenté géométriquement par un carré de Modèle:Math points.

Les Modèle:Math plus petits carrés parfaits sont :

0Modèle:2 = 0

5Modèle:2 = 25

10Modèle:2 = 100

15Modèle:2 = 225

20Modèle:2 = 400

25Modèle:2 = 625

30Modèle:2 = 900

35Modèle:2 = 1 225

40Modèle:2 = 1 600

45Modèle:2 = 2 025

50Modèle:2 = 2 500

55Modèle:2 = 3 025

60Modèle:2 = 3 600

65Modèle:2 = 4 225

1Modèle:2 = 1

6Modèle:2 = 36

11Modèle:2 = 121

16Modèle:2 = 256

21Modèle:2 = 441

26Modèle:2 = 676

31Modèle:2 = 961

36Modèle:2 = 1 296

41Modèle:2 = 1 681

46Modèle:2 = 2 116

51Modèle:2 = 2 601

56Modèle:2 = 3 136

61Modèle:2 = 3 721

66Modèle:2 = 4 356

2Modèle:2 = 4

7Modèle:2 = 49

12Modèle:2 = 144

17Modèle:2 = 289

22Modèle:2 = 484

27Modèle:2 = 729

32Modèle:2 = 1 024

37Modèle:2 = 1 369

42Modèle:2 = 1 764

47Modèle:2 = 2 209

52Modèle:2 = 2 704

57Modèle:2 = 3 249

62Modèle:2 = 3 844

67Modèle:2 = 4 489

3Modèle:2 = 9

8Modèle:2 = 64

13Modèle:2 = 169

18Modèle:2 = 324

23Modèle:2 = 529

28Modèle:2 = 784

33Modèle:2 = 1 089

38Modèle:2 = 1 444

43Modèle:2 = 1 849

48Modèle:2 = 2 304

53Modèle:2 = 2 809

58Modèle:2 = 3 364

63Modèle:2 = 3 969

68Modèle:2 = 4 624

4Modèle:2 = 16

9Modèle:2 = 81

14Modèle:2 = 196

19Modèle:2 = 361

24Modèle:2 = 576

29Modèle:2 = 841

34Modèle:2 = 1 156

39Modèle:2 = 1 521

44Modèle:2 = 1 936

49Modèle:2 = 2 401

54Modèle:2 = 2 916

59Modèle:2 = 3 481

64Modèle:2 = 4 096

69Modèle:2 = 4 761

Les nombres carrés sont les carrés parfaits non nuls, le Modèle:Mvar-ième étant Modèle:Math

Propriétés

Les mathématiciens se sont beaucoup intéressés à certaines propriétés concernant les nombres carrés. La plus connue, notamment pour sa référence au théorème de Pythagore, est l'égalité Modèle:Nobr le plus petit des triplets pythagoriciens. D'après le théorème de Fermat-Wiles, démontré en 1995, il n'y a que les nombres carrés qui peuvent former une identité comme celle des triplets pythagoriciens. Par exemple, il n'y a aucune solution à l'équation Modèle:Nobr avec Modèle:Math Modèle:Math et Modèle:Mvar entiers non nuls.

Plusieurs autres propriétés relatives aux carrés parfaits sont mentionnées dans la suite de ce chapitre, où Modèle:Math et Modèle:Mvar sont des entiers naturels.

• 1. Si Modèle:Mvar et Modèle:Mvar sont des carrés parfaits, alors le produit Modèle:Mvar est aussi un carré parfait.

• 2. Modèle:Math ; $a$ est un carré parfait si, et seulement si, tous les exposants dans sa décomposition en produit de facteurs premiers sont pairs.

• 3. Modèle:Math si Modèle:Mvar est un carré parfait et si Modèle:Mvar et Modèle:Mvar sont premiers entre eux, alors Modèle:Mvar et Modèle:Mvar sont aussi des carrés parfaits.
  Ne pas oublier la seconde condition. Par exemple : Modèle:Math mais Modèle:Math et Modèle:Math ne sont pas premiers entre eux ; Modèle:Math et Modèle:Math ne sont pas des carrés parfaits.

• 4. Modèle:Math et Modèle:Math ne sont pas des carrés parfaits.

• 5. Modèle:Math est un carré parfait si, et seulement si, le nombre de ses diviseurs est impair.

• 6. Un carré parfait ne peut se terminer que par Modèle:Math ou Modèle:Math dans le système décimal.

Attention, la réciproque n'est pas vraie : par exemple $10$ se termine par $0$ mais n'est pas un carré parfait.Modèle:DémonstrationCeci est un cas d'application des propriétés des résidus quadratiques modulo un entier. On dit qu'un entier Modèle:Mvar est un résidu quadratique modulo un entier Modèle:Mvar s'il existe un entier Modèle:Mvar tel que : $q\equiv n^{2}modm$. Ce concept permet notamment de démontrer sans calcul que certaines équations diophantiennes n'admettent pas de solution. Par exemple, avec $k$ entier, l'équation $n^2=4k+2$ n'admet pas de solution dans $\mathbb{Z}$. En effet, les résidus quadratiques modulo $4$ étant $0$ et $1$, un carré parfait ne peut pas posséder un reste égal à $2$ dans la division euclidienne par $4$.

• 7. Le Modèle:Mvar-ième nombre carré est égal à la [[Somme (arithmétique)#Autres sommes|somme des Modèle:Mvar premiers nombres impairs]] positifs:

$\sum _{i=1}^n(2i-1)=1+3+5+\dots +(2n-1)=n^2.$

Cette propriété fournit un moyen pratique pour former une table de carrés. Elle peut être représentée et utilisée sous forme de gnomons : la représentation du premier nombre carré, Modèle:Math est un point ; celle du Modèle:Mvar-ième, Modèle:Math, s'obtient en bordant deux côtés consécutifs du Modèle:Math-ième carré de points par un « L » de Modèle:Math points :

1 = 1Modèle:2

1 + 3 = 4 = 2Modèle:2

4 + 5 = 9 = 3Modèle:2

9 + 7 = 16 = 4Modèle:2

1 + 3 + 5 + 7 = 4Modèle:2

Elle est aussi utilisée comme méthode d'extraction de racine carrée, y compris avec un boulier.

Illustration de la propriété de la somme des premiers cubes pour n=5.

• 8. Le Modèle:Mvar-ième nombre carré est égal à la somme des Modèle:Mvar-ième et Modèle:Math-ième nombres triangulaires :

$\frac{n(n+1)}{2}+\frac{n(n-1)}{2}=n^2.$

• 9. La somme des Modèle:Mvar-ième et Modèle:Math-ième nombres carrés est égale au Modèle:Mvar-ième nombre carré centré.

• 10. La [[Somme (arithmétique)#Somme des premières puissances|somme des Modèle:Mvar premiers nombres carrés]] est égale au Modèle:Mvar-ième nombre pyramidal carré :

$\sum _{i=1}^n{i}^2=1^2+2^2+3^2+\dots +n^2=\frac{n(n+1)(2n+1)}{6}.$

• 11. La somme des [[Somme (arithmétique)#Somme des premières puissances|Modèle:Mvar]] premiers cubes, $\sum _{i=1}^n{i}^3$ , est un carré parfait. Plus précisément :

$\sum _{i=1}^n{i}^3={\left(\sum _{i=1}^{n}i\right)}^2={\left(\frac{n(n+1)}{2}\right)}^2$.

Calcul mental

Calculer facilement le carré d'un entier

On peut calculer mentalement les carrés des nombres entiers s'écrivant avec deux (voire trois) chiffres en notation décimale assez facilement. Soit un nombre x s'écrivant $10a+b$, avec b un chiffre non nul. On obtient son carré facilement en calculant de la façon suivante :

• $x^2=(x+b)\times a\times 10+b^2$ si b est compris entre 1 et 4,
• $x^2=a(a+1)\times 100+25$ si b est égal à 5,
• $x^2=(x-b^{\prime })\times (a+1)\times 10+b{\text{'}}^2$ si b est compris entre 6 et 9, avec $b^{\prime }=10-b$.

Cela réduit la difficulté du calcul au produit d'un nombre de deux chiffres par un nombre réduit à un chiffre, et à l'élévation au carré des nombres 1 à 4. Ainsi :

• $62^2=64\times 6\times 10+2^2=3840+4=3844$
• $65^2=6\times 7\times 100+25=4200+25=4225$
• $76^2=72\times 8\times 10+4^2=5760+16=5776$

Trouver la partie entière de la racine carrée d'un entier sans division ni multiplication

La propriété 7 permet de calculer tous les carrés d'entiers par addition d'entiers impairs. Elle permet également de connaitre la partie entière de la racine carrée d'un entier en n'utilisant que l'addition.

On procède comme suit : pour un entier quelconque $a$, on réalise progressivement l'addition des premiers nombres impairs.

Alors, pour un certain rang $n$, on a : $\sum _{i=1}^n(2i-1)=n^2⩽a<(n+1{)}^2=\sum _{i=1}^{n+1}(2i-1)$ , soit $n⩽\sqrt{a}<n+1$ . Donc la partie entière de la racine carrée $a$ est égale à $n$, qui est le nombre maximal de nombres impairs qu'on a pu additionner sans dépasser $a$, ou encore le nombre de boules formant le côté du gnomon correspondant.

Si l'on tombe exactement sur $a$, c'est que $a$ est un carré parfait, de racine carrée égale à $n$.

Carrés parfaits dans le monde réel

Carrés parfaits dans des créations humaines

Les carrés parfaits sont présents dans de très nombreux ouvrages d'algèbre et de géométrie. Comme ils peuvent être représentés par des carrés géométriques, ils se retrouvent également dans différentes réalisations humaines, notamment :

• jeux : échiquiers (carrés parfaits de 8x8), damiers (carrés parfaits de 8x8 ou 10x10), tabliers de Go (carrés parfaits de 9x9, 13x13 ou 19x19). Et le célèbre Rubik's Cube, décliné en de multiples variantes depuis sa création en 1974, se présente, dans sa forme originelle, comme un cube parfait de 3x3x3, chacune de ses six faces étant un carré parfait de 3x3.
• éléments d'architecture et de décoration : les carrelages réalisés en pose droite avec des carreaux carrés montrent des carrés parfaits pouvant atteindre une très grande taille. Certaines techniques de pose de parquet font également apparaître des carrés parfaits. De même, des plafonds à caissons carrés montrent, dès l'Antiquité, des carrés parfaits, comme à la Maison Carrée de Nîmes.

• 
  Damier, carré parfait de 10x10.
• 
  Rubik's Cube dont chaque face est un carré parfait 3x3.
• 
  Carrelage montrant des carrés parfaits de 2x2, 4x4 et 6x6.

Carrés parfaits dans la nature

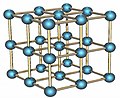
Les carrés parfaits sont présents dans la structure cristalline de certains éléments naturels, notamment ceux dont la maille constitutive est un cube, tels le polonium, le fer, le chrome,le tungstène, l'aluminium, le cuivre, l'or, l'argent, etc. La structure de ces éléments est constituée par l'association de ces mailles élémentaires pouvant former des cristaux cubiques contenant un très grand nombre d'atomes, dont chacune des six faces est un carré parfait.

• 
  Représentation de la structure cristalline du Polonium (Po): cristal cubique de 2x2x2 dont chacune des six faces est un carré parfait 2x2.
• 
  Bloc de roche contenant trois cristaux de pyrite (FeS₂). La structure cristalline de la pyrite est cubique, et les faces de ses cristaux cubiques sont des carrés parfaits.

Voir aussi

Lien externe

Carré parfait sur recreomath.qc.ca