Battement (acoustique)

Modèle:Voir homonymes En physique, le battement est une modulation périodique d'un signal constitué de la superposition de deux signaux de fréquences proches. Le terme est issu de l'acoustique ; en acoustique musicale, le battement est audible lorsque deux cordes ou tuyaux vibrent à des fréquences dont la différence est entre 0,5 et Modèle:Unité environ.

Les battements peuvent être perçus facilement en accordant un instrument capable de notes tenues. Accorder deux notes à l'unisson produit un effet particulier : tant que les deux notes ont des hauteurs voisines mais pas identiques, la différence des fréquences produit un battement ; la note résultante est modulée par un trémolo pendant que les sons interfèrent alternativement de manière constructive puis destructive. Lorsque les notes s'approchent de l'unisson, le battement ralentit puis disparaît. On se sert aussi de ce phénomène pour créer des basses d'orgue avec deux tuyaux deux fois plus courts que le nécessaire légèrement différents, dont le battement à une vingtaine de hertz crée la note basse.

Inversement, un son pur modulé en amplitude avec porteuse supprimée produit une sensation de battement tant que la fréquence de modulation est suffisamment basse ; lorsque celle-ci croît, on perçoit les deux raies latérales du spectre. On étudie par ce moyen la sélectivité fréquentielle de l'oreille.

En électronique, le battement est utilisé pour la détection synchrone.

Étude du battement

Physique

Les sons des instruments de musique capables de produire des notes comportent principalement une onde de forme sinusoïdale, dont la fréquence correspond à la hauteur musicale. L'analyse mathématique montre que la somme de deux sinusoïdes équivaut à une sinusoïde de fréquence égale à la moyenne de leurs fréquences, modulée en amplitude par une sinusoïde de fréquence égale à la demi-différence de leurs fréquences. C'est ce qui se passe lorsqu'on mélange les ondes acoustiques de deux notes.

Psychoacoustique du battement

Cependant, l'écoute d'un mélange de deux sons de fréquences suffisamment proches pour qu'on entende un battement montre que la fréquence de ce battement est la différence de fréquence des deux sons (et non la demi-différence).

Perception des battements et du son différentiel

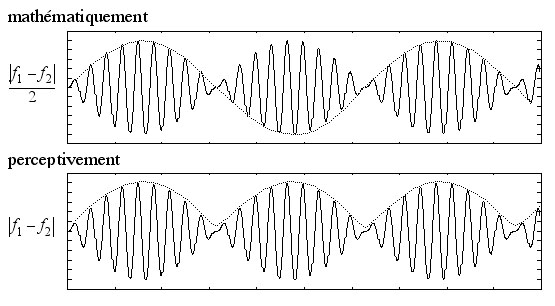
L'oreille humaine, en effet, perçoit des écarts d'intensité sonore de moins de 10 % et est capable de différencier plusieurs centaines de fréquences sonores. En nécessaire contrepartie, le temps nécessaire à cette analyse la rend insensible aux différences de situation temporelle des composantes du son.

Quand on étudie l'onde sonore résultante du mélange de deux ondes sinusoïdales, on s'aperçoit qu'à deux instants distants d'une moitié de la période du trémolo calculée mathématiquement (celle de la demi-différence des fréquences des composantes), les ondes ne diffèrent que par un léger décalage temporel (un décalage de phase) dépendant uniquement de la différence de fréquence entre les composantes. On n'entend pas cette différence ; les deux moitiés de la période mathématique paraissent identiques, et donc on entend une note modulée par un trémolo de fréquence égale à la différence entre les fréquences des composantes.

Fichier:SoundBeats1.ogg Fichier:SoundBeats2.ogg Modèle:Exemple

Limites du phénomène des battements

Les règles de composition de deux ondes sinusoïdales sont valables quelles que soient les fréquences de chacune d'elles. Elles ne produisent un battement audible que si

• l'intensité sonore des deux composantes est approximativement égale, de sorte que l'une ne masque pas l'autre ;
• le battement n'est pas trop lent (une période supérieure à 5 secondes ne s'entend pas) ;
• le battement n'est pas trop rapide (lorsque sa fréquence croît, on finit par percevoir les deux composantes).

Quand on ne perçoit pas de battement, on se trouve dans le cas plus général d'un son résultant.

Usage du phénomène de battement

Battement des harmoniques

Les notes de musique émises par les instruments musicaux ne sont pas des sinusoïdes pures émises par des instruments de laboratoire. Elles sont des compositions de fréquences harmoniques, c'est-à-dire multiples d'une fréquence fondamentale par un nombre entier. Ces partiels peuvent aussi se combiner en faisant entendre des battements.

Accord des instruments

Le phénomène de battement s'entend très bien lorsqu'une personne accorde un instrument à corde (par exemple une guitare) : on entend une vibration du son, due au mélange des sons émis par les deux cordes pincées ensemble. C'est ce phénomène qui permet d'effectuer, simplement à l'oreille, l'accord des instruments de musique : un intervalle est pur lorsqu'on n'entend plus aucun battement.

Dans la tradition musicale de la musique occidentale, on considère comme purs les intervalles entre les notes qui sont dans un rapport de fréquence égal à une fraction simple (3/2, 4/3, etc.). Cependant, pour des raisons techniques autant qu'esthétiques, on utilise la gamme à tempérament égal, où une proportion unique gouverne l'écart entre chaque note successive : un demi-ton correspond à environ +5,6 % en fréquence, de sorte que 12 demi-tons font une octave. Avec cette gamme, comme l'a montré l'exemple du do et du sol ci-dessus, les rapports entre les notes ne sont plus exactement harmoniques. Des méthodes d'accordage emploient le comptage des battements pour placer les notes exactement à l'intervalle tempéré où ils doivent se trouver dans un instrument à sons fixes comme le piano.

Justesse et battements dans la musique occidentale

L'existence d'un battement reconnu permet d'effectuer l'accord ou l'intonation. Par exemple, l'emploi du tempérament égal cause le battement des tierces (voir article : Justesse des tierces).

Modèle:Exemple La tierce majeure n'est jamais utilisée pure qu'en musique ancienne ; la qualité de son battement permet aux instrumentistes de s'assurer qu'ils jouent juste.

Des intervalles moins consonants, bien que « justes », tels que les seconde ou sixte mineures, peuvent également produire des battements qui sont constitutifs de leur nature. C'est là la raison de leur faible consonance.

Calculs et démonstrations

Sommation de sinusoïdes de même amplitude

Soit un signal composé de la somme de deux sinusoïdes

$s(t)=\sin ({\omega }_{1}t+{\phi }_1)+\sin ({\omega }_{2}t+{\phi }_2)$

La pulsation ω, égale à 2π × fréquence, est la caractéristique de chacune des composantes. On sait (voir formules de Simpson) que

$\sin p+\sin q=2\sin \frac{p+q}{2}\cdot \cos \frac{p-q}{2}$

et donc

$\begin{array}{cc}s(t)& =\sin ({\omega }_{1}t+{\phi }_1)+\sin ({\omega }_{2}t+{\phi }_2)\\ & =2\sin (\frac{({\omega }_1+{\omega }_2)t}{2}+\frac{{\phi }_1+{\phi }_2}{2})\cos (\frac{({\omega }_1-{\omega }_2)t}{2}+\frac{{\phi }_1-{\phi }_2}{2})\end{array}$

si l'on pose

$\{\begin{array}{cc}{\omega }_m=\frac{{\omega }_1+{\omega }_2}{2}& \text{moyenne des pulsations}\\ {\omega }_d=\frac{{\omega }_1-{\omega }_2}{2}& \text{demi-différence des pulsations}\\ {\phi }_m=\frac{{\phi }_1+{\phi }_2}{2}& \text{moyenne des phases}\\ {\phi }_d=\frac{{\phi }_1-{\phi }_2}{2}& \text{demi-différence des phases}\end{array}$

on a

$\begin{array}{cc}s(t)& =\sin ({\omega }_{1}t+{\phi }_1)+\sin ({\omega }_{2}t+{\phi }_2)\\ & =2\sin ({\omega }_{m}t+{\phi }_m)\cdot \cos ({\omega }_{d}t+{\phi }_d)\end{array}$

soit en toutes lettres

La somme de deux sinusoïdes équivaut à une sinusoïde de fréquence égale à la moyenne de leurs fréquences, multipliée (ou modulée) par une sinusoïde de fréquence égale à la demi-différence de leurs fréquences.

Ce signal n'est périodique que si les fréquences composantes sont des multiples d'une même fréquence fondamentale par des nombres entiers.

Sommation de sinusoïdes d'amplitudes quelconques

Si maintenant, les deux sinusoïdes n'ont pas la même amplitude:

$s(t)=\alpha \sin ({\omega }_{1}t+{\phi }_1)+\beta \sin ({\omega }_{2}t+{\phi }_2)$

Avec les mêmes relations que précédemment, on a

$\begin{array}{cc}s(t)& =\alpha \sin ({\omega }_{1}t+{\phi }_1)+\beta \sin ({\omega }_{2}t+{\phi }_2)\\ & =(\alpha +\beta )\sin (\frac{({\omega }_1+{\omega }_2)t}{2}+\frac{{\phi }_1+{\phi }_2}{2})\cos (\frac{({\omega }_1-{\omega }_2)t}{2}+\frac{{\phi }_1-{\phi }_2}{2})+(\alpha -\beta )\cos (\frac{({\omega }_1+{\omega }_2)t}{2}+\frac{{\phi }_1+{\phi }_2}{2})\sin (\frac{({\omega }_1-{\omega }_2)t}{2}+\frac{{\phi }_1-{\phi }_2}{2})\end{array}$

Avec les mêmes notations que précédemment, on a:

$\begin{array}{cc}s(t)& =\alpha \sin ({\omega }_{1}t+{\phi }_1)+\beta \sin ({\omega }_{2}t+{\phi }_2)\\ & =(\alpha +\beta )\sin ({\omega }_{m}t+{\phi }_m)\cdot \cos ({\omega }_{d}t+{\phi }_d)+(\alpha -\beta )\cos ({\omega }_{m}t+{\phi }_m)\cdot \sin ({\omega }_{d}t+{\phi }_d)\end{array}$

Différence de phase

Intrigués par la différence entre la perception par l'oreille, qui entend un battement de fréquence égale à la différence de fréquence entre les composantes, et le résultat du calcul mathématique, nous cherchons à comparer le signal de la première demi-période du trémolo de l'onde somme (du temps 0 au temps π/ω_d) au signal de la seconde demi-période, π/ω_d plus tard.

Posons donc

$t^{\prime }=t+\frac{\pi }{{\omega }_d}$

nous avons

$\begin{array}{cc}s(t^{\prime })& =2\sin ({\omega }_m(t+\frac{\pi }{{\omega }_d}))\cdot \cos ({\omega }_d(t+\frac{\pi }{{\omega }_d}))\\ & =-2\sin ({\omega }_m\cdot t+\frac{\pi {\omega }_m}{{\omega }_d})\cdot \cos \left({\omega }_{d}t\right)\end{array}$

On voit que s(t') ne diffère de s(t) que par une différence de phase de (1+ ω_m/ω_d)π qui ne dépend que de l'écart relatif des fréquences.

L'oreille, dont l'organe de perception des sons, les cellules cillées de l'organe de Corti, se comportent en quelque sorte comme des filtres résonateurs à bande passante très étroite, ne peuvent en même temps définir une hauteur précise et un temps précis. Elles sont donc nécessairement insensibles à la phase. Il n'est donc pas surprenant que nous ne sentions aucune différence entre les deux parties de la période mathématique du battement.

Annexes

Bibliographie

• Modèle:Ouvrage
• Modèle:Chapitre
• Modèle:Ouvrage

Articles connexes

• Son résultant
• Justesse des tierces
• Le moiré, en optique, offre une « visualisation » du battement.
• Consonance (musique)