Méthode des trapèzes

Principe de la méthode : l'aire sous la courbe représentative de Modèle:Mvar est approchée par l'aire sous une droite affine (en rouge).

Animation montrant comment la méthode des trapèzes converge vers la valeur exacte lorsque le nombre d’itérations augmente.

En analyse numérique, la méthode des trapèzes est une méthode pour le calcul numérique d'une intégrale$\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x$ s'appuyant sur l'interpolation linéaire par intervalles.

Intervalle unique

Le principe est d'assimiler la région sous la courbe représentative d'une fonction Modèle:Mvar définie sur un segment Modèle:Math à un trapèze et d'en calculer l'aire Modèle:Mvar :

$T=(b-a)\frac{f(a)+f(b)}{2}.$

Erreur

En analyse numérique l'erreur est par convention la différence entre la valeur exacte (limite) et son approximation par un nombre fini d'opérations. (Modèle:Citation)..

L'erreur d'approximation par un polynôme de Taylor est le reste de la série de Taylor, et l'erreur de quadrature correspond à la différence entre l'aire totale sous la courbe et la somme des aires des trapèzes Modèle:,Modèle:,.

En métrologie, l'erreur est définie comme la différence entre valeur approchée et valeur réelle, soit l'opposé de l'erreur définie dans cet article, qui, en métrologie, porte le nom de correction.

Pour une fonction à valeurs réelles, deux fois continûment différentiable sur le segment Modèle:Math, l'erreur est de la forme

$\underset{a}{\overset{b}{\int }}f(x)\mathrm{d}x-(b-a)\frac{f(a)+f(b)}{2}=-\frac{(b-a{)}^3}{12}{f}^{″}(\xi )$

pour un certain $\xi \in [a,b]$ (méthode du premier ordre).

Dans le cas d'une fonction convexe (dérivée seconde positive), l'aire du trapèze est donc une valeur approchée par excès de l'intégrale.

Intervalles multiples

Pour obtenir de meilleurs résultats, on découpe l'intervalle Modèle:Math en n intervalles plus petits et on applique la méthode sur chacun d'entre eux. Bien entendu, il suffit d'une seule évaluation de la fonction à chaque nœud :

$\underset{a}{\overset{b}{\int }}f(x)dx=\frac{b-a}{n}(\frac{f(a)+f(b)}{2}+\sum _{k=1}^{n-1}f(a+k\frac{b-a}{n}))+R_n(f)$

Le terme Modèle:Math est l'erreur de quadrature et vaut : $-\frac{(b-a{)}^3}{12n^2}{f}^{″}(\xi )$ pour un $\xi \in [a,b]$

La méthode des trapèzes revient à estimer l'intégrale d'une fonction comme l'intégrale de son interpolation linéaire par intervalles.

Exemple d'approximation d'une fonction par des trapèzes

Voici le découpage d'une fonction Modèle:Mvar que l'on veut intégrer sur l'intervalle Modèle:Math

$f(x)=1,1+\ln (\mathrm{e}-\frac{x}{100}+\frac{3}{5}\tanh (\ln (x+10^{-7})+1))\cos (x)+\frac{2}{5}{(x-\frac{\cos (3x)}{5})}^2+\frac{11}{100}\sqrt{2+2x}\sin (\frac{44}{25}(4+3\sqrt{x})x-\frac{19}{20}{x}^5)-{\mathrm{e}}^{\frac{x}{3}}$

Découpage pour différentes valeurs de n (2,8 et 16).

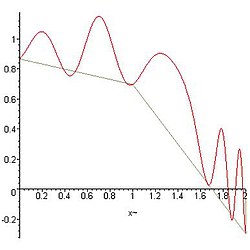
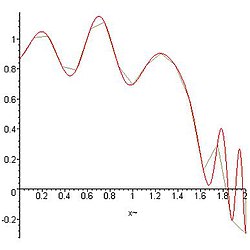
Divers théorèmes

Théorème : Si f est 2 fois continûment différentiable sur Modèle:Math, la méthode des trapèzes est convergente sur $C^2([a,b])$.
Théorème : La méthode des trapèzes est stable pour les méthodes composites (à intervalles multiples).

Lien avec les autres méthodes d'intégration

La méthode des trapèzes est la première des formules de Newton-Cotes, avec deux nœuds par intervalle. Sa rapidité de mise en œuvre en fait une méthode très employée. Cependant, la méthode de Simpson permet une estimation plus précise d'un ordre pour un coût souvent raisonnable.

Comme tout estimateur basé sur un pas de calcul, la méthode des trapèzes est compatible avec la méthode d'accélération de convergence de Romberg.

Voir aussi

Articles connexes

• Calcul intégral
• Formule d'Euler-Maclaurin

Liens externes

• Modèle:Lien web