Onde de détonation Taylor-von Neumann-Sedov

L'onde de détonation Taylor-von Neumann-Sedov est une solution auto-similaire du problème de détonation décrite simultanément par Geoffrey Ingram Taylor, John von Neumann et Leonid Sedov pendant la Seconde Guerre mondialeModèle:,.

Ces études ont été effectuées afin d'estimer les effets d'un engin nucléaire indépendamment par :

• Geoffrey Ingram Taylor pour le Royaume-Uni en juin 1941,
• John von Neumann pour les États-Unis, également en juin 1941,
• Leonid Sedov, à pareille époque, pour l'URSS. La publication de ses travaux date de 1946.

La théorie

Cette théorie décrit les effets d'une explosion, donc de la création et de la propagation d'un choc et d'un écoulement associé, à partir d'une distance où le détail de la source ne joue plus de rôle et où celle-ci peut être entièrement décrite par une énergie $E$ issue du point en $r=0$.

La propagation se fait dans une atmosphère pour laquelle on peut prendre  $p_0=0$  compte tenu de la valeur importante  $p_1$  derrière le choc créé  $p_1>>p_0$. Il n'en va pas de même pour la masse volumique : en effet les relations de Rankine-Hugoniot prédisent une limite à la masse volumique

$\lim {\mathrm{\backslash limits}}_{Ma\to \mathrm{\infty }}\frac{{\rho }_1}{{\rho }_0}=\frac{\gamma +1}{\gamma -1}$

où $\gamma$ est l'indice adiabatique du milieu ($\gamma =1.4$ pour l'air à basse température).

On suppose que le paramètre pertinent est le seul nombre adimensionnel possible pour ce problème où interviennent les variables $t,r,{\rho }_0,E$. Ce nombre est

$r{\left(\frac{{\rho }_0}{E{t}^2}\right)}^{\frac{1}{5}}$.

En particulier ceci est vrai pour le rayon de propagation

$R(t)=\beta {\left(\frac{E{t}^2}{{\rho }_0}\right)}^{\frac{1}{5}}$

D'où la vitesse de propagation

$V_{\mathrm{\infty }}=\frac{\mathrm{d}R}{\mathrm{d}t}=\frac{2\beta }{5}{\left(\frac{E}{{\rho }_0{t}^3}\right)}^{1/5}=\frac{2R}{5t}$

Les relations de Rankine-Hugoniot permettent de calculer les quantités en amont du choc

$v_1=\frac{2}{\gamma +1}{V}_{\mathrm{\infty }},p_1=\frac{2}{\gamma +1}{\rho }_0{V}_{\mathrm{\infty }}^2,{\rho }_1\approx {\rho }_0\frac{\gamma +1}{\gamma -1}$

${\rho }_1$ est donc approximativement constant.

Solution autosimilaire

Solution autosimilaire pour $\gamma =7/5$ et $\beta =1.033$.

Le système obéit aux équations d'Euler en géométrie sphérique

$\begin{array}{cc}\frac{\partial v}{\partial t}+v\frac{\partial v}{\partial r}+\frac{1}{\rho }\frac{\partial p}{\partial r}& =0\\ \frac{\partial \rho }{\partial t}+\frac{\partial (\rho v)}{\partial r}+\frac{2\rho v}{r}& =0\\ (\frac{\partial }{\partial t}+v\frac{\partial }{\partial r})\ln \frac{p}{{\rho }^{\gamma }}& =0\end{array}$

En $r=R(t)$ les valeurs sont celles définies ci-dessus.

La pression peut être remplacée par la vitesse du son  $c(r,t)=\sqrt{\gamma p/\rho }$.

On introduit les variables sans dimensionModèle:,

$\xi =\frac{r}{R(t)},V(\xi )=\frac{5tv}{2r},G(\xi )=\frac{\rho }{{\rho }_0},Z(\xi )=\frac{25t^2{c}^2}{4r^2}$.

Les conditions derrière le choc $\xi =1$ deviennent

$V(1)=\frac{2}{\gamma +1},G(1)=\frac{\gamma +1}{\gamma -1},Z(1)=\frac{2\gamma (\gamma -1)}{(\gamma +1{)}^2}$

La résolution des équations d'Euler est assez longue. On peut la simplifier à partir de la conservation de l'énergie. La relation entre $Z$ et $V$ peut être déduite directement de la conservation de l'énergie. La solution étant auto-semblable l'énergie à l'intérieur de la sphère de rayon $\xi <1$ quelconque, grossissant à la vitesse $2r/5t$, est constante. L'énergie qui quitte la sphère de rayon $r$ dans l'intervalle $dt$ du fait de la vitesse de gaz $v$ est  $4\pi r^2\rho v(h+v^2/2)\mathrm{d}t$ où  $h=c^2/(\gamma -1)$ est l'enthalpie volumique du gaz. Dans cet intervalle de temps le rayon croît avec la vitesse $v_n$ pour arriver à une énergie  $4\pi r^2\rho v_n(e+v^2/2)\mathrm{d}t$ où  $e=c^2/\gamma (\gamma -1)$ est l'énergie interne par unité de volume. D'où

$Z=\frac{\gamma (\gamma -1)(1-V)V^2}{2(\gamma V-1)}$

Les équations de continuité et de conservation de l'énergie deviennent

$\begin{array}{cc}\frac{\mathrm{d}V}{\mathrm{d}\ln \xi }-(1-V)\frac{\mathrm{d}\ln G}{\mathrm{d}\ln \xi }& =-3V\\ \frac{\mathrm{d}\ln Z}{\mathrm{d}\ln \xi }-(\gamma -1)\frac{\mathrm{d}\ln G}{\mathrm{d}\ln \xi }& =-\frac{5-2V}{1-V}\end{array}$

En exprimant $\mathrm{d}V/\mathrm{d}\ln \xi$ et $\mathrm{d}\ln G/\mathrm{d}V$ comme fonctions de $V$ seulement et en intégrant on obtient

$\begin{array}{cc}{\xi }^5& ={[\frac{1}{2}(\gamma +1)V]}^{-2}{\{\frac{\gamma +1}{7-\gamma }[5-(3\gamma -1)V]\}}^{{\nu }_1}{[\frac{\gamma +1}{\gamma -1}(\gamma V-1)]}^{{\nu }_2},\\ G& =\frac{\gamma +1}{\gamma -1}{[\frac{\gamma +1}{\gamma -1}(\gamma V-1)]}^{{\nu }_3}{\{\frac{\gamma +1}{7-\gamma }[5-(3\gamma -1)V\}}^{{\nu }_4}{[\frac{\gamma +1}{\gamma -1}(1-V)]}^{{\nu }_5}\end{array}$

où

${\nu }_1=-\frac{13{\gamma }^2-7\gamma +12}{(3\gamma -1)(2\gamma +1)},{\nu }_2=\frac{5(\gamma -1)}{2\gamma +1},{\nu }_3=\frac{3}{2\gamma +1},{\nu }_4=-\frac{{\nu }_1}{2-\gamma },{\nu }_5=-\frac{2}{2-\gamma }$

La constante $\beta$ qui exprime la position du choc peut être déduite de la conservation de l'énergie

$E=\underset{0}{\overset{R}{\int }}\rho [v^2/2+c^2/\gamma (\gamma -1)]4\pi r^2\mathrm{d}r$

On obtient

${\beta }^5\frac{16\pi }{25}\underset{0}{\overset{1}{\int }}G[V^2/2+Z/\gamma (\gamma -1)]{\xi }^4\mathrm{d}\xi =1$

On peut alors revenir aux variables physiques

$\rho /{\rho }_1=G(\gamma -1)/(\gamma +1),v/v_1=\xi V(\gamma +1)/2,p/p_1={\xi }^{2}GZ(\gamma +1)/(2\gamma )$

et en déduire la température $T$

$T/T_1={\xi }^{2}Z(\gamma +1{)}^2/[2\gamma (\gamma -1)]$

Comportement asymptotique dans la partie centrale

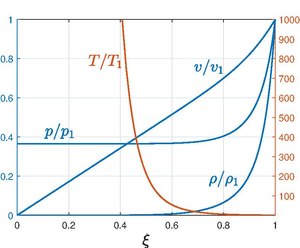
L'analyse de la solution permet de connaître le comportement asymptotique pour lequel la masse volumique décroît rapidement derrière le choc et la pression vers une valeur limite $p_c\approx 0.37p_1$ (voir figure)

$\frac{\rho }{{\rho }_1}\sim {\xi }^{3/(\gamma -1)},\frac{p}{p_1}\to p_c,\frac{T}{T_1}\sim {\xi }^{-3/(\gamma -1)}\text{lorsque}\xi \to 0$

On rappelle que ${\rho }_1$ dépend du temps comme $p_1\sim t^{-6/5}$. Dans les variables physiques

$\rho \sim r^{3/(\gamma -1)}{t}^{-6/5(\gamma -1)},p\to p_c{t}^{-6/5},T\sim r^{-3/(\gamma -1)}{t}^{(6/5)(2-\gamma )/(\gamma -1)}\text{lorsque}r\to 0.$

La vitesse varie linéairement dans la partie centrale.

$\frac{v}{v_1}\sim \xi \text{lorsque}\xi \to 0$

et son comportement asymptotique est donné par

$v\sim r{t}^{1/5}\text{lorsque}r\to 0$

Comportement en temps long

L'analyse ci-dessus n'est plus valide lorsque  $p_1\to p_0$, phase dans laquelle se forme une partie en dépression en aval du choc. Dans ce cas on ne peut plus définir un seul nombre adimensionnel caractéristique et l'auto-similarité n'est plus vérifiée. Il existe une méthode pour aller plus loin dans les méthodes analytiques mais de nos jours on fait plutôt appel au calcul numériqueModèle:,Modèle:,

Solution numérique pour diverses géométries

Des calculs numériques ont permis d'établir une loi valable pour toute géométrie (plane, cylindrique, sphérique) :

$t=\frac{1}{q}{\left(\frac{E}{B{\rho }_0}\right)}^{-\frac{1}{2}}{R}^q$

où B est un coefficient dépendant de la géométrie :

$\gamma$	sphérique $q=\frac{5}{2}$	cylindrique $q=\frac{4}{2}$	plan $q=\frac{3}{2}$
7/5	5.33	3.94	1.22
5/3	3.08	2.26	0.678

En géométrie cylindrique

Le problème de la ligne explosive a été résolu par Leonid Sedov, A. Sakurai et S. C. Lin. Le nombre adimensionnel pertinent est ici

$r{\left(\frac{{\rho }_0}{E{t}^2}\right)}^{\frac{1}{4}}$

D'où le rayon de propagation :

$R(t)=\beta {\left(\frac{E}{{\rho }_0}\right)}^{\frac{1}{4}}{t}^{\frac{1}{{}^2}}$

Pour  $\gamma =\frac{7}{5}$  l'approximation numérique décrite ci-dessus donne  $\beta ={\left(\frac{4}{B}\right)}^{\frac{1}{4}}\approx 1.00$ 

La vitesse de propagation s'écrit :

$V_{\mathrm{\infty }}=\frac{\beta }{2}{\left(\frac{E}{{\rho }_0}\right)}^{\frac{1}{4}}{t}^{-\frac{1}{{}^2}}=\frac{Rt}{2}$

On peut en déduire le saut de pression en utilisant une approximation des relations de Rankine-Hugoniot :

$p-p_0={\rho }_0{V}_{\mathrm{\infty }}^2(1-\frac{\rho }{{\rho }_0})\approx \frac{2}{\gamma +1}{\rho }_0{V}_{\mathrm{\infty }}^2=\frac{{\beta }^4}{2(\gamma +1)}E{R}^{-2}\approx 0.212E{R}^{-2}$

La surpression est proportionnelle à l'énergie et décroît avec le carré de la distance à la source.

Ouvrages

• Modèle:Ouvrage
• Modèle:Ouvrage

Voir aussi

• Modèle de détonation de Zeldovich-von Neumann-Döring