Équation de Boltzmann quantique

LModèle:'équation de Boltzmann quantique, également connue sous le nom dModèle:'équation d'Uehling-Uhlenbeck, est l'extension de l'équation de Boltzmann classique qui donne l'évolution temporelle hors d'équilibre d'un système de particules quantiques en interaction. L'équation de Boltzmann quantique se distingue formellement de celle classique par le terme de collision, qui donne l'évolution de la distribution de quantité de mouvement d'un gaz localement homogène causée par les collisions binaires entre les molécules ; ce terme de collision, qui prend en compte des contraintes de la mécanique quantique, a été initialement formulé par Lothar Nordheim (1928), et par Modèle:Lien et George Uhlenbeck (1933).

L'équation de Boltzmann-Uehling-Uhlenbeck (BUU)

Forme générale de l'équation de Boltzmann

La forme générale de l'équation de Boltzmann est la suivante :

$\frac{df(𝐫,𝐩;t)}{dt}+\{f(𝐫,𝐩;t),H(𝐫,𝐩)\}={\left(\frac{\partial f}{\partial t}\right)}_{coll}$

$f(𝐫,𝐩;t)$ est la distribution à un corps dans la hiérarchie BBGKY qui donne la densité de probabilité pour une particule quelconque du système de se situer en un point $(𝐫,𝐩)$ de l'espace des phases. $H(𝐫,𝐩)$ est l'hamiltonien du système ; $\{,\}$ est le crochet de Poisson.

Lorsque les forces dérivent d'un potentiel, et en explicitant le second terme, on obtient la forme la plus usuelle de l'équation complète

$[\frac{\partial }{\partial t}+𝐯\cdot {\mathrm{\nabla }}_r+𝐅\cdot {\mathrm{\nabla }}_p]f(𝐫,𝐩,t)={𝐈}_{coll}[f](𝐫,𝐩)$

avec le produit scalaire ( . ) et ${\mathrm{\nabla }}_r$ l'opérateur usuel gradient pour les positions, qui se formule de manière analogue pour les moments. $𝐅$ représente les forces appliquées sur les particules de la distribution : soit forces extérieures, soit forces entre les particules dans la limite du champ moyen.

${𝐈}_{coll}[f]$ est l'opérateur de collision, qui rend compte des interactions directes entre les particules, en général les collisions binaires. La mécanique quantique doit être prise en compte dans la forme exacte de ${𝐈}_{coll}[f]$, qui dépend de la physique du système à modéliser .

Lorsque l'on traite des systèmes de fermions, le principe d'exclusion de Pauli impose des contraintes fortes sur la densité dans l'espace des phases (voir Physique semi-classique) qui doit satisfaire pour tout volume élémentaire $\mathrm{\Delta }𝐫\mathrm{\Delta }𝐩$

$f(𝐫,𝐩,t)\mathrm{\Delta }𝐫\mathrm{\Delta }𝐩<\frac{2}{{\hslash }^3}\mathrm{\Delta }𝐫\mathrm{\Delta }𝐩$

Dans un régime purement hamiltonien (sans collisions binaires), si la contrainte est vérifiée initialement, elle le sera durant toute l'évolution du système (théorème de Liouville) ; il est donc nécessaire que le terme de collisions prenne en compte cette limitation.

Terme de collision de Uehling et Uhlenbeck (UU)

La forme la plus usuelle est le terme de Uehling-Uhlenbeck (UU) pour les fermions : $${\left(\frac{\partial f(p_1)}{\partial f}\right)}_{coll}=\frac{g}{2{\pi }^2}\frac{h^3}{m^2}\int ...\int d{𝐩}_{\mathrm{𝟐}}d{𝐩}_{\mathrm{𝟑}}d{𝐩}_{\mathrm{𝟒}}\delta ({ϵ}_1^2+{ϵ}_2^2-{ϵ}_3^2-{ϵ}_4^2)\delta ({𝐩}_{\mathrm{𝟏}}+{𝐩}_{\mathrm{𝟐}}-{𝐩}_{\mathrm{𝟑}}-{𝐩}_{\mathrm{𝟒}})\frac{d\sigma }{d\mathrm{\Omega }}[(1-f_1)(1-f_2)f_3{f}_4-(1-f_3)(1-f_4)f_1{f}_2]$$

g est le facteur de dégénérescence des niveaux ($g=2$ pour des fermions de spin 1/2, $g=4$ pour les nucléons avec l'isospin). Les termes indicés $f_i\equiv f({𝐫}_i,{𝐩}_i;t);{ϵ}_i={𝐩}_i^2/2m$ caractérisent les particules en voie d'entrée (indices 1 et 2) et en sortie (indices 3,4) ; la section efficace (probabilité) de collision est $d\sigma /d\mathrm{\Omega }$. Le terme de collision UU établit la conservation de l'énergie et des impulsions dans un choc élastique (les distributions de Dirac $\delta$) et le respect du principe d'exclusion de Pauli.

La fonction de distribution est ici normalisée à un maximum égal à l'unité, c'est donc le nombre d'occupation local dans l'espace des phases.

En factorisant le terme de collisions, on obtient la forme synthétique :

${\left(\frac{\partial f}{\partial t}\right)}_{coll}=W^{+}(1-f)-W^{-}f$

avec le terme de gain $W^{+}$ qui fait croitre le taux d'occupation local jusqu'à la limite $f\to 1$ bloquée par le principe de Pauli ; le terme de perte $W^{-}$fait décroître le taux d'occupation.

Extension au cas des bosons

Le terme de collisions ci-dessus, défini pour des fermions, est un cas particulier d'une forme générale qui inclut les particules classiques et les bosons. On peut généraliser les termes de blocage spécifique aux fermions dans l'équation ci-dessus, en prenant en compte respectivement les statistiques classiques, de Bose-Einstein et de Fermi-Dirac : ils s'écrivent alors :

$(1+\theta f_1)(1+\theta f_2)f_3{f}_4-(1+\theta f_3)(1+\theta f_4)f_1{f}_2$

avec $\theta =0$ pour les particules classiques, $\theta =1$ pour les bosons et $\theta =-1$ pour les fermions. On obtient alors :

${\left(\frac{\partial f}{\partial t}\right)}_{coll}=W^{+}(1+\theta f)-W^{-}f$

Dans la suite, on se limitera à l'équation pour les fermions.

Blocage de Pauli pour les fermions

Dans l'espace des moments, pour conserver l'énergie et l'impulsion, les collisions élastiques entre 2 particules A et B, de moments respectifs ${𝐩}_A$ et ${𝐩}_B$, se traduisent par une rotation aléatoire de leur moment relatif ${𝐩}_A-{𝐩}_B$ (voir l'article Équation de Boltzmann). Le principe de Pauli en mécanique quantique, implique que pour que la collision soit possible, l'espace des phases pour les impulsions finales $𝐩{\text{'}}_A$ et $𝐩{\text{'}}_B$ ne soit pas occupé (voir figure). En mécanique classique, la rotation aléatoire peut donc prendre toutes les valeurs de 0 à $2\pi$ ; en mécanique quantique, seules les rotations conduisant à des états inoccupés sont possibles et ont donc une probabilité fortement réduite.

Illustration dans l'espace des moments des effets du terme de collisions dans un système hors équilibre (les 2 cercles grisés -en rouge et bleu- représentent l'espace initial des impulsions du système) ; on considère la collision élastique de 2 particules A et B). À gauche, le cas classique, après la collision, les moments des 2 particules peuvent prendre les valeurs sur l'ensemble du cercle en vert (exemple A' et B'). À droite, le cas quantique, seul l'arc du cercle en vert, est permis ; les autres étant bloqués par le principe de Pauli (un des états ou les deux sont occupés).

Dans le cas de la figure, on considère un système hors équilibre, constitué de deux distributions de fermions identiques (cercles grisés) en interaction (la figure pourrait correspondre à une réaction nucléaire entre 2 noyaux lourds à des énergies supérieures à Modèle:Unité par nucléon).

Pour la paire de fermions A et B, à gauche, la totalité du cercle (en vert) est accessible avec le terme de collision classique ; seule une très petite partie (en vert à droite) est possible avec le terme de collisions UU ; la probabilité de collisions est réduite d'un ordre de grandeur.

L'équation de Boltzmann quantique s'applique donc à des systèmes fortement hors équilibre (modes collectifs de grande amplitude, collisions…).

Solutions asymptotiques

Le terme de collision dans l'équation quantique de Boltzmann donne un comportement irréversible à l'évolution du système. L'équation détermine une solution d'équilibre :

$f_{equ}=\frac{W^{+}}{W^{+}+W^{-}}=\frac{1}{1+\exp \left(\frac{ϵ-\mu }{T}\right)}$

Celle-ci satisfait la statistique de Fermi-Dirac. Elle exprime la probabilité pour les particules d'avoir une énergie $ϵ$ en fonction de 2 paramètres, le niveau de Fermi $\mu$ et la température $T$. Elle correspond au maximum de l'entropie du système.

Comme son équivalent classique, l'équation quantique détermine une flèche du temps ; c'est-à-dire qu'après un temps suffisamment long, elle conduit à une distribution d'équilibre qui n'évolue plus macroscopiquement.

Bien que la mécanique quantique soit microscopiquement réversible dans le temps, l'équation quantique de Boltzmann donne un comportement irréversible car l'information de phase est ignorée, seul le nombre moyen d'occupation des états quantiques est conservé. La solution de l'équation quantique de Boltzmann est donc une bonne approximation du comportement exact du système sur des échelles de temps courtes par rapport au temps de récurrence de Poincaré, ce qui n'est généralement pas une limitation sévère, car le temps de récurrence de Poincaré peut être plusieurs fois l'âge de l'univers même dans de petits systèmes.

Résolution numérique

Comme son équivalent classique, l'équation BUU n'a de solutions analytiques que dans des cas très spécifiques. Dans la pratique, on la résout par des méthodes numériques, soit par des méthodes eulériennes sur réseau, soit par des méthodes lagrangiennes (voir la section « Les méthodes de résolution numérique directe » de l'article Équation de Boltzmann).

Comme elle traite des problèmes hors équilibre avec une grande extension dans l'espace des phases; les méthodes lagrangiennes sont particulièrement adaptées. De plus, ces méthodes permettent une simulation directe du terme de collision UU (voir infra).

Méthodes pseudo-particulaires

Elles sont basées sur le fait que la distribution quantique dans l'espace des phases $f(𝐫,𝐩,t)\ge 0$ d'un système de A fermions, supposée positive, peut être approchée par celle d'un système de $nA$ (pseudo-)particules suivant des trajectoires classiques (avec $n\gg 1$).

Cela revient à projeter la fonction sur une base dépendant du temps $g(𝐫,𝐩,t)$, par convolution avec une fonction de poids $w(𝐫,𝐩)$, indépendante du temps et strictement positive $f(𝐫,𝐩,t)=w(𝐫,𝐩)*g(𝐫,𝐩,t),$ où les fonctions $g(𝐫,𝐩,t)$ doivent être solutions de l'équation de Boltzmann sans collisions et représenter une base la plus complète possible de l'espace des phases. La solution de l'équation est donnée par les trajectoires classiques des fonctions $g(𝐫,𝐩,t)$.

En pratique, on effectue un échantillonnage de type Monte-Carlo et $f(𝐫,𝐩,t)\approx \frac{1}{n}{\sum }_{i=1}^{nA}g(𝐫-{𝐫}_i(t))g(𝐩-{𝐩}_i(t)),$ où les $({𝐫}_{𝐢},{𝐩}_{𝐢})$ sont les coordonnées des pseudo-particules dans l'espace des phases. Selon le contexte, les fonctions g utilisées sont soit des distributions de Dirac, soit des gaussiennes. Le calcul explicite des collisions entre les pseudo-particules nécessite une renormalisation de leur section efficace par rapport à celle des particules physiques.

Applications

Physique des semi-conducteurs

L'équation de Boltzmann est utilisée en physique des semi-conducteurs. Un modèle typique d'un semi-conducteur peut être construit sur les hypothèses suivantes à la base de l'équation de Boltzmann :

1. La distribution des électrons est spatialement homogène à une approximation raisonnable (donc toute dépendance x peut être supprimée) ;
2. Le potentiel externe est fonction uniquement de la position et isotrope dans l'espace p, et donc $𝐅$ peut être mis à zéro sans perdre davantage de généralité ;
3. Le gaz est suffisamment dilué pour que les interactions à trois corps entre les électrons puissent être ignorées.

Physique nucléaire

À partir des années 1980, avec le développement des accélérateurs permettant d'étudier les réactions entre noyaux lourds de haute énergie, une part importante de la physique nucléaire a été consacrée à l'étude de la matière nucléaire très loin de l'équilibre ; l'étude théorique de ces réactions est très largement basée sur les équations du type Boltzmann quantique.

Exemple d'utilisation de l'équation de Boltzmann quantique en physique nucléaire (réaction très inélastique Sn+Xe à 35MeV/u). Les courbes de niveau représentent la densité nucléaire projetée sur le plan de réaction ; en couleurs pour le projectile, pour montrer les échanges de nucléons lors de la réaction.

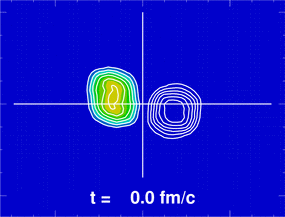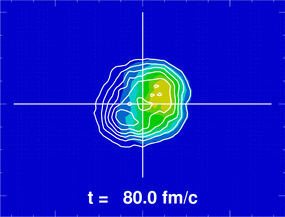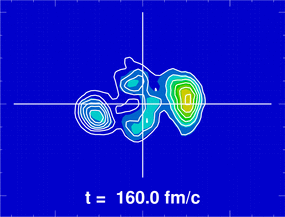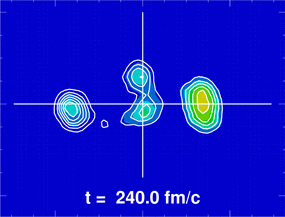
La figure ci-contre donne un exemple d'utilisation de l'équation de Boltzmann quantique en physique nucléaire (réaction très inélastique Sn+Xe à 35 MeV/u).

Les courbes de niveau représentent la densité de probabilité des nucléons projetée sur le plan de réaction (cadre de 80 x 60 fermis) ; les courbes sont tracées en couleurs pour le projectile, pour montrer les échanges de nucléons lors de la réaction. L'unité de temps est le fm/c : $3fm/c=10^{-23}s$. La solution de l'équation de Boltzmann donne accès aux échanges de nucléons et d'énergie dans la réaction et aux trajectoires des fragments produits.

Physique relativiste

Aux énergies relativistes pour les systèmes baryoniques, il est nécessaire : d'une part de rendre l'équation invariante par la transformation de Lorentz et d'autre part, de tenir compte de la production de nouvelles particules dont les seuils de production sont dépassés (collisions nucléaires à très haute énergie, milieux stellaire...).

Voir aussi

• Équation de Boltzmann
• Mécanique quantique dans l'espace des phases
• Espace des phases
• Mécanique hamiltonienne