Fonction méromorphe

La fonction Gamma d'Euler est une fonction méromorphe car elle est analytique sur tout le plan complexe, sauf en des pôles isolés.

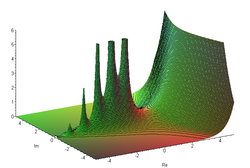
En mathématiques, et plus précisément en analyse complexe, une fonction méromorphe est une fonction holomorphe dans tout le plan complexe, sauf éventuellement sur un ensemble de points isolés dont chacun est un pôle pour la fonction. Cette terminologie s'explique par le fait qu'en grec ancien, meros (μέρος) signifie « partie » et holos (ὅλος) signifie « entier ».

Propriétés

Le théorème de factorisation de Hadamard affirme que toute fonction méromorphe peut s'écrire comme le rapport de deux fonctions entières (dont celle du dénominateur n'est pas identiquement nulle) : les pôles de la fonction correspondent aux zéros du dénominateur. En d'autres termes, l'ensemble des fonctions méromorphes est le corps des fractions de l'anneau des fonctions holomorphes.

En matière de surface de Riemann, une fonction méromorphe est comme une fonction holomorphe du plan complexe dans la sphère de Riemann qui n'est pas la constante infinie. Les pôles correspondent aux nombres complexes qui sont envoyés sur ∞.

On étend par ailleurs la définition de « fonction méromorphe » à tout ouvert de $ℂ$. C'est ainsi que les exemples de fonctions non méromorphes (sur $ℂ$) ci-dessous sont néanmoins des fonctions méromorphes sur un petit disque centré en 1/2.

Exemples

Des exemples de fonctions méromorphes sont :

• toutes les fonctions rationnelles comme $\frac{z^3-2z+1}{z^5+3z-1}$,
• les fonctions $\frac{{\mathrm{e}}^z}{z}$, $\tan (z)$, $\frac{\sin (z)}{(z-1{)}^2}$ ou même la fonction gamma d'Euler et la fonction zêta de Riemann.

Des exemples de fonctions non méromorphes sont :

• toutes les fonctions algébriques (non rationnelles) (ex. : $\sqrt{z}$) et plus généralement toute fonction présentant un point de branchement algébrique ;
• toutes les fonctions ayant un point de branchement logarithmique (ex. : $\ln (z)$, le dilogarithme) ;
• toutes les fonctions ayant une singularité essentielle ailleurs qu'à l'infini (ex. : ${\mathrm{e}}^{\frac{1}{z}}$) ;
• toutes les fonctions ayant une accumulation de singularités (ex. : la série génératrice des partitions).