Équation ZFK

L'équation ZFK, abréviation de Zeldovich-Frank-Kamenetskii, est une équation de réaction–diffusion qui modélise la propagation de la flamme prémélangée. L'équation doit son nom à Iakov Zeldovitch et à David Frank-Kamenetskii qui l'ont dérivée en 1938. Elle est également connue sous le nom d'équation de Nagumo. L'équation est analogue à l'équation KPP-Fisher mais contient un comportement exponentiel pour le terme de réaction qui modifie de manière importante la vitesse de propagation de l'onde progressive solution de l'équation. Sous forme adimensionnelle, l'équation s'écrit :

$\frac{\partial \theta }{\partial t}=\frac{{\partial }^2\theta }{\partial x^2}+\omega (\theta )$

avec une forme typique pour $\omega$ donnée par

$\omega =\frac{{\beta }^2}{2}\theta (1-\theta )e^{-\beta (1-\theta )}$

où $\theta \in [0,1]$ est la variable dépendante adimensionnelle (typiquement la température réduite) et $\beta$ est le nombre de Zeldovitch. Dans le régime ZFK $\beta \gg 1$. L'équation se réduit à l'équation KPP-Fisher pour $\beta \ll 1$ et donc $\beta \ll 1$ correspond au régime KPP. La vitesse de propagation minimale $U_{min}$ (qui est généralement la vitesse asymptotique) d'une onde progressive dans le régime ZFK est donnée par :

$U_{ZFK}\propto \sqrt{2\underset{0}{\overset{1}{\int }}\omega (\theta )d\theta }$

tandis que dans le régime KPP, elle est donnée par :

$U_{KPP}=2\sqrt{{\frac{d\omega }{d\theta }|}_{\theta =0}}$

Onde progressive

Solution numérique de l'équation ZFK.

Comme dans le cas de l'équation KPP-Fisher il existe une solution de type onde progressive. Supposons que cette onde se déplace de droite à gauche avec une vitesse constante $U$, alors dans le système de coordonnées attachée à l'onde $z=x+Ut$, le problème devient stationnaire. L'équation ZFK se réduit à :

$U\frac{d\theta }{dz}=\frac{d^2\theta }{d{z}^2}+\frac{{\beta }^2}{2}\theta (1-\theta )e^{-\beta (1-\theta )}$

avec les conditions aux limites $\theta (-\mathrm{\infty })=0$ et $\theta (+\mathrm{\infty })=1$. Celles-ci sont satisfaites par la solution suffisamment régulière pour que la dérivée $d\theta /dz$ s'annule également lorsque $z\to \pm \mathrm{\infty }$. Comme l'équation est invariante par translation dans la direction $z$, une condition supplémentaire, par exemple $\theta (0)=1/2$, peut être utilisée pour fixer l'emplacement de l'onde. La vitesse de l'onde $U$ est obtenue dans le cadre de la solution, constituant ainsi un problème de valeur propre non linéaire.

Solution asymptotique

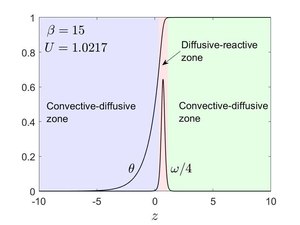
La limite $\beta \to \mathrm{\infty }$ peut être analysée en utilisant l'asymptotique des grandes énergies d'activation. Étant donné que $\beta$ est grand, le terme $e^{-\beta (1-\theta )}$ rendra le terme de réaction pratiquement nul sauf si $1-\theta \sim 1/\beta$. Le terme de réaction s'annulera également lorsque $\theta =0$ et $\theta =1$. Il est donc clair que $\omega$ est négligeable partout sauf dans une couche mince proche de la frontière $\theta =1$. Le problème est donc divisé en trois régions, une région interne diffusive-réactive flanquée de chaque côté par deux régions externes convectives-diffusives.

Régions externes

Le problème des régions externes est donné par :

$U\frac{d\theta }{dz}=\frac{d^2\theta }{d{z}^2}$

La solution satisfaisant la condition $\theta (-\mathrm{\infty })=0$ est $\theta =e^{Uz}$. Cette solution est également conçue pour satisfaire $\theta (0)=1$ (un choix arbitraire) pour fixer l'emplacement de l'onde quelque part dans le domaine car le problème est invariant par translation dans la direction $z$. Comme $z\to 0^{-}$, la solution externe se comporte comme $\theta =1+Uz+\cdots$ ce qui implique $d\theta /dz=U+\cdots .$

La solution satisfaisant la condition $\theta (+\mathrm{\infty })=1$ est $\theta =1$ et donc $d\theta /dz=0$.

Nous pouvons voir que bien que $\theta$ soit continue à $z=0$, $d\theta /dz$ présente un saut à $z=0$. La transition entre les dérivées est décrite par la région interne.

Région interne

Dans la région interne où $1-\theta \sim 1/\beta$, le terme de réaction n'est plus négligeable. Pour étudier la structure de la couche interne, on prolonge la coordonnée pour englober le point $z=0$ car c'est là que $\theta$ s'approche de l'unité selon la solution externe et une variable prolongée $\eta =\beta z,\mathrm{\Theta }=\beta (1-\theta )$. En substituant ces variables dans l'équation générale et en ne retenant que les termes d'ordre dominant, on obtient :

$2\frac{d^2\mathrm{\Theta }}{d{\eta }^2}=\mathrm{\Theta }{e}^{-\mathrm{\Theta }}$

La condition limite $\eta \to -\mathrm{\infty }$ vient du comportement local de la solution externe obtenue précédemment, qui, écrite dans les coordonnée de la zone interne devient $\mathrm{\Theta }\to -U\eta =+\mathrm{\infty }$ et $d\mathrm{\Theta }/d\eta =-U$ et pour $\eta \to +\mathrm{\infty }$ on obtient $\mathrm{\Theta }=d\mathrm{\Theta }/d\eta =0$. La première intégrale de l'équation ci-dessus après avoir imposé ces conditions aux limites devient :

$\begin{array}{cc}{{\left(\frac{d\mathrm{\Theta }}{d\eta }\right)}^2|}_{\mathrm{\Theta }=\mathrm{\infty }}-{{\left(\frac{d\mathrm{\Theta }}{d\eta }\right)}^2|}_{\mathrm{\Theta }=0}& =\underset{0}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Theta }{e}^{-\mathrm{\Theta }}d\mathrm{\Theta }\\ U^2& =1\end{array}$

ce qui implique $U=1$. Il ressort clairement de la première intégrale que le carré de la vitesse de l'onde $U^2$ est proportionnel à la valeur intégrée (par rapport à $\theta$) de $\omega$ (bien entendu, dans la grande limite $\beta$, seule la zone intérieure contribue à cette intégrale). La première intégrale après avoir substitué $U=1$ est donnée par :

$\frac{d\mathrm{\Theta }}{d\eta }=-\sqrt{1-(\mathrm{\Theta }+1)\exp (-\mathrm{\Theta })}$

Malgré sa simplicité cette équation ne possède pas de solution analytique.

Transition KPP-ZFK

Courbe noire : $U(\beta )$ calculé numériquement ; courbe rouge : $U_{KPP}=\sqrt{2}\beta e^{-\beta /2}$ ; courbe bleue : $U_{ZFK}=1$.

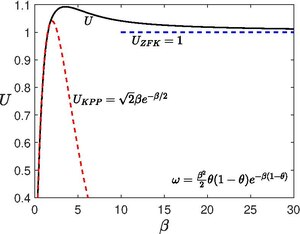
Dans le régime KPP, $U_{min}=U_{KPP}.$ Pour le terme de réaction utilisé ici, la vitesse KPP applicable pour $\beta \ll 1$ est donnée par :

$U_{KPP}=2\sqrt{{\frac{d\omega }{d\theta }|}_{\theta =0}}=\sqrt{2}\beta e^{-\beta /2}$

Dans le régime ZFK $U_{ZFK}=1$. L'intégration numérique de l'équation pour différentes valeurs de $\beta$ a montré qu'il existe une valeur critique ${\beta }_{*}=1,64$ telle que seulement pour $\beta \le {\beta }_{*}$, $U_{min}=U_{KPP}.$ Pour $\beta \ge {\beta }_{*}$, $U_{min}$ est supérieur à $U_{KPP}$. Lorsque $\beta \gg 1$, $U_{min}$ s'approche de $U_{ZFK}=1$, se rapprochant ainsi du régime ZFK. La région entre le régime KPP et le régime ZFK est appelée zone de transition KPP–ZFK.

La valeur critique dépend du modèle de réaction, par exemple on obtient :

${\beta }_{*}=3.04\text{pour}\omega \propto (1-\theta )e^{-\beta (1-\theta )}$

${\beta }_{*}=5.11\text{pour}\omega \propto (1-\theta {)}^2{e}^{-\beta (1-\theta )}$

Modèle de Clavin–Liñán

Pour prédire analytiquement la transition KPP–ZFK, Paul Clavin et Amable Liñán ont proposé un modèle linéaire par morceaux :

$\omega (\theta )=\{\begin{array}{ccc}\theta & \text{si}& 0\le \theta \le 1-ϵ\\ h(1-\theta )/{ϵ}^2& \text{si}& 1-ϵ\le \theta \le 1\end{array}$

où $h$ et $ϵ$ sont des constantes. La vitesse KPP du modèle est $U_{KPP}=2$, tandis que la vitesse ZFK est obtenue comme $U_{ZFK}=\sqrt{h}$ dans la double limite $ϵ\to 0$ et $h\to \mathrm{\infty }$ qui imite une forte augmentation de la réaction près de $\theta =1$.

Pour ce modèle, il existe une valeur critique $h_{*}=1-{ϵ}^2$ telle que :

$\{\begin{array}{cc}h<h_{*}:& U_{min}=U_{KPP},\\ h>h_{*}:& U_{min}=\frac{h/(1-ϵ)+1-ϵ}{\sqrt{h/(1-ϵ)-ϵ}},\\ h\gg h_{*}:& U_{min}\to U_{ZFK}\end{array}$