Suite spectrale

En algèbre homologique et en topologie algébrique, une suite spectrale est un moyen de calculer des groupes de cohomologie par approximations successives. Ces suites ont été introduites par Jean Leray en 1946, et sont depuis devenues un outil technique majeur en géométrie algébrique, complexe, ou en algèbre homologique. Par exemple, la Modèle:Lien permet d'obtenir des informations sur les groupes d'homotopie des sphères.

Les séquences spectrales sont réputées difficiles à appréhender en raison de la grande quantité d'informations qu'elles mettent en jeu. Les cas les plus faciles à traiter sont ceux où la suite spectrale dégénère, ce qui signifie qu'une approximation supplémentaire ne produira aucune nouvelle information.

Historique et motivation

Motivé par des problèmes de topologie algébrique, Jean Leray a introduit la notion de faisceau et a chercher à calculer les groupes de cohomologie de faisceaux. C'est à cette occasion que Leray introduit la notion de suite spectrale. Étant donné un faisceau $ℱ$ sur un espace topologique $X$ et une application continue $f:X\to Y$, on peut pousser en avant $ℱ$, donnant un faisceau $f^{*}ℱ$ sur $Y$. Leray a constaté que les groupes de cohomologie du poussé en avant forment un complexe de chaînes naturel, de sorte que l'on peut prendre la cohomologie de la cohomologie. Il ne s'agit pas de la cohomologie du faisceau $ℱ$, mais celle-ci s'en rapproche en un certain sens. La cohomologie de la cohomologie forme à nouveau un complexe de chaînes, on opère le même procédé et ainsi de suite. À la limite de ce processus, le résultat est essentiellement la cohomologie du faisceau initial.

On s'est rendu compte que la technique de calcul de Leray était un exemple d'un phénomène plus général. Bien que leur importance théorique ait reculé depuis l'introduction des catégories dérivées, elles restent l'outil de calcul cohomologique le plus systématique et efficace qui soit.

Définition

Suite spectrale homologique

Soit une catégorie abélienne (e.g. les Modèle:Lien vers une page d'homonymie sur un anneau), et un entier non négatif $r_0$. Une suite spectrale homologique est une collection $\{E_r,d_r{\}}_{r\ge r_0}$ d'objets $E_r$ et d'endomorphismes $d_r:E_r\to E_r$, tel que pour tout $r\ge r_0$

1. $d_r\circ d_r=0$,
2. $E_{r+1}\cong H_{*}(E_r,d_r)$, l'homologie de $E_r$ par rapport à $d_r$.

Par habitude, les isomorphismes sont supprimés et on écrit $E_{r+1}=H_{*}(E_r,d_r)$. Un objet $E_r$ est appelé une « page », ou encore un « terme » ; les endomorphismes $d_r$ les « différentielles ». Et, $E_{r+1}$ est appelé « l'objet dérivé » de $E_r$.

Suite spectrale bigraduée

La page E₂ d'une suite spectrale cohomologique.

En réalité, les suites spectrales se produisent principalement dans la catégorie des Modèle:Lien vers une page d'homonymie bigradués sur un anneau R, c'est-à-dire que chaque page est un R-module bigradué $E_r=\underset{p,q\in {\mathbb{Z}}^2}{⨁}{E}_r^{p,q}$. Une suite spectrale cohomologique est alors une suite $\{E_r,d_r{\}}_{r\ge r_0}$ de R-modules bigradués $\{E_r^{p,q}{\}}_{p,q}$, et pour chaque module une famille d'endomorphismes $d_r=(d_r^{p,q}:E_r^{p,q}\to E_r^{p+r,q-r+1}{)}_{p,q\in {\mathbb{Z}}^2}$ de bidegré $(r,1-r)$. On demande pour $r\ge r_0$ :

1. $d_r^{p+r,q-r+1}\circ d_r^{p,q}=0$,
2. $E_{r+1}\cong H^{*}(E_r,d_r)$.

Selon la suite spectrale, la première age peut avoir un degré égal à r = 0, 1 ou 2. Par exemple, pour le suite spectrale d'un complexe filtré décrite ci-dessous, on a r₀ = 0, mais pour la suite spectrale de Grothendieck, on a r₀ = 2. Modèle:Clr

Suite spectrale d'un complexe de chaînes

On se place dans l'hypothèse non gradué. La suite spectrale associée à un complexe de chaînes C_• donne l'exemple le plus simple dans ce cas. Soit d la différentielle associée au complexe. Soit r₀ = 0, et E₀ étant définit par C_•. Par conséquent, E₁ est le complexe H(C_•) : Le i-ème terme du complexe E₁ calcul le i-ème groupe de (co)homologie de C_•. La seule différentielle naturelle sur ce nouveau complexe est la différentielle nulle : d₁ = 0. Cela force $E_2$ à être égal à $E_1$. La suite spectrale dégénère en page 1. Pour résumer :

• E₀ est le complexe C_•,
• E₁ est le complexe H(C_•) pour r ≥ 1.

L'information de la suite spectrale est concentrée en degré 0 et 1 : aller calculer les pages supérieures ne sert pas. Il faut habituellement une structure supplémentaire sur les E_r, pour obtenir des informations utiles en pages supérieures.

Illustration

Une suite spectrale bigraduée contient une grande quantité d'information à suivre. Il existe des illustrations qui rendent la structure de la suite spectrale plus claire. Nous avons trois indices, r, p et q. Un objet $E_r$ peut être vu comme la $r$-ième page d'un livre à carreaux. Sur ces pages, p désigne la direction horizontale et q la verticale. À chaque point du réseau, nous avons l'objet $E_r^{p,q}$. Passer à la page suivante signifie prendre l'homologie (resp. la cohomologie), c'est-à-dire que la $r+1$-ième page est un sous-quotient de la $r$-ième page. Dans le cas homologique, les différentielles ont un bidegré (−r, r − 1), donc n diminue de un d'une page à l'autre. Dans le cas cohomologique, n est augmenté de un.

Quatre pages d'une suite spectrale cohomologique. Les flèches rouges dénote les différentielles d'une suite concentrée en le premier quadrant (i.e. où seuls les objets du premier quadrant sont non nuls).

Propriétés

Propriétés catégorielles

L'ensemble des suite spectrales cohomologiques forment une catégorie. Une flèche dans cette catégorie $f:E\to E^{\prime }$ est par définition une collection de morphismes $f_r:E_r\to E{\text{'}}_r$ compatibles avec la différentielles, i.e. $f_r\circ d_r=d{\text{'}}_r\circ f_r$, et avec l'isomorphisme entre la cohomologie de la r-ième page et la (r+1)-ième page de E et E', c'est-à-dire: $f_{r+1}(E_{r+1})=f_{r+1}(H(E_r))=H(f_r(E_r))$. Dans le cas bigradué, les morphismes doivent de plus conserver la graduation: $f_r(E_r^{p,q})\subset {E{\text{'}}_r}^{p,q}.$

Structure multiplicative

Un cup-produit donne une structure d'anneau à un groupe de cohomologie, le transformant en un anneau de cohomologie. Ainsi, il est naturel de considérer une structure d'anneaux sur la suite spectrale. Soit $E_r^{p,q}$ une suite spectrale de type cohomologique. On dit qu'elle a une structure multiplicative si

1. $E_r$ est une algèbre différentielle graduée (ou bigraduée) ;
2. La multiplication sur $E_{r+1}$ est induite par celle sur $E_r$.

Un exemple est donné par la suite spectrale de Serre cohomologique associée à une fibration $F\to E\to B$, lorsque le groupe de coefficients est un anneau RModèle:SfnModèle:,Modèle:Sfn. La structure multiplicative peut être très utile pour calculer des différentielles de la suiteModèle:Sfn.

Constructions de suites spectrales

Les suite spectrales peuvent être construites de différentes manières. En topologie algébrique, un couple exact est peut-être l’outil de construction le plus courant. En géométrie algébrique, les suites spectrales sont généralement construites à partir de filtrations de complexes de cochaînes.

Suite spectrale d'un couple exact

Une première construction de suites spectrales est la méthode des couples exacts de William Massey, devenus courants en topologie algébrique ; mais bien moins en algèbre.

Pour définir des couples exacts, on se donne une catégorie abélienne. Comme ce-dessus, dans la pratique, il s'agit généralement de modules bigradués sur un anneau. Un couple exact est une paire d'objets (A, C), munie de trois homomorphismes entre ces objets : f : A → A, g : A → C et h : C → A vérifiants les conditions d'exactitudes :

• Im f = Ker g
• Im g = Ker h
• Im h = Ker f

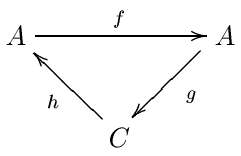
On notera cette donnée (A, C, f, g, h), représentée par un triangle. le terme C correspond à la première page E₀ de la suite spectrale et A est une donnée auxiliaire.

Pour passer à la page suivante, on définit le couple dérivé. Soit :

• d = g o h
• A' = f(A)
• C' = Ker d / Im d
• f' = f|_A', la restriction de f à A'
• h' : C' → A' induit par h.
• g' : A' → C' et définie comme suit: Pour tout a dans A', on note a = f(b) pour un certain b dans A. g'(a) est défini comme étant l'image de g(b) dans C'.

Il est immédiat de vérifier que le couple (A', C', f', g', h') est exact. C' correspond au terme E₁ de la suite spectrale. On définit par récurrence la suite (A⁽ⁿ⁾, C⁽ⁿ⁾, f⁽ⁿ⁾, g⁽ⁿ⁾, h⁽ⁿ⁾).

Les différentielles de la suite spectrale sont données par,d_n = g⁽ⁿ⁾ o h⁽ⁿ⁾ et E_n = C⁽ⁿ⁾.

Exemples de suites spectrales

• Modèle:LienModèle:Sfn - calculant la (co)homologie d'une fibration.
• Modèle:Lien - calculant la (co)homologie en K-théorie.
• Modèle:Lien

Suite spectrale d'un complexe filtré

Une méthode courante de construction de suite spectrale provient d'un complexe de cochaînes filtré, car celui-ci induit naturellement un objet biggradué. Soit un complexe de cochaînes $(C^{\bullet },d)$ avec une filtration descendante, $...\supset F^{-2}{C}^{\bullet }\supset F^{-1}{C}^{\bullet }\supset F^0{C}^{\bullet }\supset F^1{C}^{\bullet }\supset F^2{C}^{\bullet }\supset F^3{C}^{\bullet }\supset ...$. On impose que les différentielles du complexe soit compatible avec la filtration, i.e. $d(F^p{C}^n)\subset F^p{C}^{n+1}$, et que la filtration soit exhaustive, c'est-à-dire que l'union de l'ensemble des $F^p{C}^{\bullet }$ est égal au complexe entier $C^{\bullet }$. Il existe une suite spectrale en posant$E_0^{p,q}=F^p{C}^{p+q}/F^{p+1}{C}^{p+q}$ et $E_1^{p,q}=H^{p+q}(F^p{C}^{\bullet }/F^{p+1}{C}^{\bullet })$. On supposera aussi que la filtration est séparée, c'est-à-dire que l'intersection des ensembles $F^p{C}^{\bullet }$ est nulle.

La filtration est utile car elle donne une mesure de proximité de zéro : à mesure que p augmente, $F^p{C}^{\bullet }$ se « rapproche » de plus en plus de zéro.

Construction de la suite

$C^{\bullet }$ n'est munie que d'une seule filtration, nous construisons donc d'abord un objet doublement gradué pour la première page de la suite spectrale. On note :

$Z_{-1}^{p,q}=Z_0^{p,q}=F^p{C}^{p+q}$

$B_0^{p,q}=0$

$E_0^{p,q}=\frac{Z_0^{p,q}}{B_0^{p,q}+Z_{-1}^{p+1,q-1}}=\frac{F^p{C}^{p+q}}{F^{p+1}{C}^{p+q}}$

$E_0=\underset{p,q\in 𝐙}{⨁}{E}_0^{p,q}$

Puisque nous avons supposé que les applications sont compatibles à la filtration, $E_0$ est un objet bigradué et on a une différentielle $d_0$ sur $E_0$. Pour obtenir $E_1$, on prend l'homologie de $E_0$.

${\overline{Z}}_1^{p,q}=\ker d_0^{p,q}:E_0^{p,q}\to E_0^{p,q+1}=\ker d_0^{p,q}:F^p{C}^{p+q}/F^{p+1}{C}^{p+q}\to F^p{C}^{p+q+1}/F^{p+1}{C}^{p+q+1}$

${\overline{B}}_1^{p,q}=\text{im }{d}_0^{p,q-1}:E_0^{p,q-1}\to E_0^{p,q}=\text{im }{d}_0^{p,q-1}:F^p{C}^{p+q-1}/F^{p+1}{C}^{p+q-1}\to F^p{C}^{p+q}/F^{p+1}{C}^{p+q}$

$E_1^{p,q}=\frac{{\overline{Z}}_1^{p,q}}{{\overline{B}}_1^{p,q}}=\frac{\ker d_0^{p,q}:E_0^{p,q}\to E_0^{p,q+1}}{\text{im }{d}_0^{p,q-1}:E_0^{p,q-1}\to E_0^{p,q}}$

$E_1=\underset{p,q\in 𝐙}{⨁}{E}_1^{p,q}=\underset{p,q\in 𝐙}{⨁}\frac{{\overline{Z}}_1^{p,q}}{{\overline{B}}_1^{p,q}}$

Noter que ${\overline{Z}}_1^{p,q}$ et ${\overline{B}}_1^{p,q}$ peuvent être écrits comme images dans $E_0^{p,q}$ de

$Z_1^{p,q}=\ker d_0^{p,q}:F^p{C}^{p+q}\to C^{p+q+1}/F^{p+1}{C}^{p+q+1}$

$B_1^{p,q}=(\text{im }{d}_0^{p,q-1}:F^p{C}^{p+q-1}\to C^{p+q})\cap F^p{C}^{p+q}$

de sorte que l'on puisse écrire

$E_1^{p,q}=\frac{Z_1^{p,q}}{B_1^{p,q}+Z_0^{p+1,q-1}}.$

$Z_1^{p,q}$ sont les éléments dont le degré dans la filtration augmentent de un par la différentielle, et $B_1^{p,q}$ sont les images des éléments dont le degré dans la filtration n'augmente pas par la différentielle. Cela suggère la definition de $Z_r^{p,q}$ et $B_r^{p,q}$ :

$Z_r^{p,q}=\ker d_0^{p,q}:F^p{C}^{p+q}\to C^{p+q+1}/F^{p+r}{C}^{p+q+1}$

$B_r^{p,q}=(\text{im }{d}_0^{p-r+1,q+r-2}:F^{p-r+1}{C}^{p+q-1}\to C^{p+q})\cap F^p{C}^{p+q}$

$E_r^{p,q}=\frac{Z_r^{p,q}}{B_r^{p,q}+Z_{r-1}^{p+1,q-1}}$

avec la relation

$B_r^{p,q}=d_0^{p,q}(Z_{r-1}^{p-r+1,q+r-2}).$

Pour que $d_r$ soit bien définie sur chaque $E_r$ et donnant l'homologie en passant à $E_{r+1}$, l'application

$d_r^{p,q}:E_r^{p,q}\to E_r^{p+r,q-r+1}$

est définie par restriction de $d$ définie sur $C^{p+q}$ au sous-objet $Z_r^{p,q}$. On vérifie aisément que l'homologie selon cette différentielle de $E_r$ est $E_{r+1}$, donnant ainsi une suite spectrale. Seulement, la définition de $d_r$ n'est pas explicite.

Exemples de suites spectrales

• Modèle:Lien
• Peut être utilisée pour la construction des modules de Hodge mixtes.

Convergence, dégénérescence

Soit E_r une suite spectrale, partant de r = 1. Il existe donc une suite de sous-objets :

$0=B_0\subset B_1\subset B_2\subset \dots \subset B_r\subset \dots \subset Z_r\subset \dots \subset Z_2\subset Z_1\subset Z_0=E_1$

tels que $E_r\simeq Z_{r-1}/B_{r-1}$; on pose en effet $Z_0=E_1,B_0=0$ et $Z_r,B_r$ tels que $Z_r/B_{r-1},B_r/B_{r-1}$ sont le noyau et l'image de $E_r\stackrel{d_r}{\to }{E}_r.$ On pose alors $Z_{\mathrm{\infty }}={\cap }_r{Z}_r,B_{\mathrm{\infty }}={\cup }_r{B}_r$ et$E_{\mathrm{\infty }}=Z_{\mathrm{\infty }}/B_{\mathrm{\infty }}$, le terme limite. (Un tel $E_{\mathrm{\infty }}$ n'existe pas forcément dans la catégorie, mais existe presque toujours en pratique ; due à la finitude de l'union.)

Termes de convergence

On dit qu'une suite converge faiblement s'il existe un objet gradué $H^{\bullet }$ avec une filtration $F^{\bullet }{H}^n$ pour tout $n$, et pour tout $p$ il existe un isomorphisme $E_{\mathrm{\infty }}^{p,q}\cong F^p{H}^{p+q}/F^{p+1}{H}^{p+q}$. La suite converge à $H^{\bullet }$ si la filtration $F^{\bullet }{H}^n$ est séparée (i.e. ${\cap }_p{F}^p{C}^{\bullet }=0$). On note

$E_r^{p,q}{\Rightarrow }_p{E}_{\mathrm{\infty }}^n$

pour signifier que pour p + q = n, $E_r^{p,q}$ converge vers $E_{\mathrm{\infty }}^{p,q}$. On dit qu'une suite spectrale $E_r^{p,q}$ aboutit à $E_{\mathrm{\infty }}^{p,q}$ si pour tout $p,q$ on a un entier $r(p,q)$ tel que pour tout $r\ge r(p,q)$, $E_r^{p,q}=E_{r(p,q)}^{p,q}$. Alors $E_{r(p,q)}^{p,q}=E_{\mathrm{\infty }}^{p,q}$ est le terme limite. La suite spectral dégénèrer à $r_0$ si les différentielles $d_r^{p,q}$ sont nulles pour tout $r\ge r_0$. On le note:

$E_r^{p,q}{\Rightarrow }_p{E}_{\mathrm{\infty }}^{p,q}$

Il est usuel d'écrire à droite $E_2^{p,q}$, la plupart des suites spectrales aboutissants en deuxième page.

Exemples de dégénérescence

Suite spectrale d'un complexe filtré, suite

On repart de la construction à partir du complexe de cochaînes $(C^{\bullet },d)$ avec filtration descendante. On remarque la suite d'inclusion

$Z_0^{p,q}\supseteq Z_1^{p,q}\supseteq Z_2^{p,q}\supseteq \cdots \supseteq B_2^{p,q}\supseteq B_1^{p,q}\supseteq B_0^{p,q}$

On peut alors se demander si, en définissant

$Z_{\mathrm{\infty }}^{p,q}=\bigcap _{r=0}^{\mathrm{\infty }}{Z}_r^{p,q},$

$B_{\mathrm{\infty }}^{p,q}=\bigcup _{r=0}^{\mathrm{\infty }}{B}_r^{p,q},$

$E_{\mathrm{\infty }}^{p,q}=\frac{Z_{\mathrm{\infty }}^{p,q}}{B_{\mathrm{\infty }}^{p,q}+Z_{\mathrm{\infty }}^{p+1,q-1}}.$

$E_{\mathrm{\infty }}^{p,q}$ serait un candidat naturel pour le terme limite. Pour décrire plus en détail l'aboutissement de la suite spectrale, notons que nous avons les formules :

$Z_{\mathrm{\infty }}^{p,q}=\bigcap _{r=0}^{\mathrm{\infty }}{Z}_r^{p,q}=\bigcap _{r=0}^{\mathrm{\infty }}\ker (F^p{C}^{p+q}\to C^{p+q+1}/F^{p+r}{C}^{p+q+1})$

$B_{\mathrm{\infty }}^{p,q}=\bigcup _{r=0}^{\mathrm{\infty }}{B}_r^{p,q}=\bigcup _{r=0}^{\mathrm{\infty }}(\text{im }{d}^{p,q-r}:F^{p-r}{C}^{p+q-1}\to C^{p+q})\cap F^p{C}^{p+q}$

Puisque la suite est séparée, les noyaux décroisent en r jusqu'à$Z_{\mathrm{\infty }}^{p,q}=\ker (F^p{C}^{p+q}\to C^{p+q+1})$. Pour $B_{\mathrm{\infty }}^{p,q}$, rappelons que la suite a été supposée exhaustive. Les images croissent jusqu'à$B_{\mathrm{\infty }}^{p,q}=\text{im }(C^{p+q-1}\to C^{p+q})\cap F^p{C}^{p+q}$. On en déduit finalement que

$E_{\mathrm{\infty }}^{p,q}={\text{gr}}_p{H}^{p+q}(C^{\bullet })$,

c'est-à-dire que la suite spectrale abouti vers la p-ième partie graduée du (p+q)-ième groupe d'homologie de C. Si la suite spectrale converge, on en déduit que :

$E_r^{p,q}{\Rightarrow }_p{H}^{p+q}(C^{\bullet })$

Suites exactes longues

En utilisant la séquence spectrale d’un complexe filtré, nous pouvons déduire l’existence de suites exactes longues. Soit une suite exacte courte de complexes de cochaînes 0 → A^• → B^• → C^• → 0, et f^• : A^• → B^•. On obtient naturellement la suite de cohomologie Hⁿ(A^•) → Hⁿ(B^•) → Hⁿ(C^•) exacte au centre. On filtre le complexe B^• comme suit :

$F^0{B}^n=B^n$

$F^1{B}^n=A^n$

$F^2{B}^n=0$

Donnant

$E_0^{p,q}=\frac{F^p{B}^{p+q}}{F^{p+1}{B}^{p+q}}=\{\begin{array}{cc}0& \text{si }p<0\text{ ou }p>1\\ C^q& \text{si }p=0\\ A^{q+1}& \text{si }p=1\end{array}$

$E_1^{p,q}=\{\begin{array}{cc}0& \text{si }p<0\text{ ou }p>1\\ H^q(C^{\bullet })& \text{si }p=0\\ H^{q+1}(A^{\bullet })& \text{si }p=1\end{array}$

La différentielle est de bidegrée (1, 0), donc d_0,q : H^q(C^•) → H^q+1(A^•). Le lemme du serpent A^• → B^• → C^• donne une suite de complexes :

$\cdots \to H^q(B^{\bullet })\to H^q(C^{\bullet })\to H^{q+1}(A^{\bullet })\to H^{q+1}(B^{\bullet })\to \cdots$

Il reste à montrer que cette suite est exacte en les groupes associés à A et C. Notons que la suite dégénère en E₂ (par degré de la différentielle). Par conséquent, le terme E₂ est égal à E_∞ :

$E_2^{p,q}\cong {\text{gr}}_p{H}^{p+q}(B^{\bullet })=\{\begin{array}{cc}0& \text{si }p<0\text{ ou }p>1\\ H^q(B^{\bullet })/H^q(A^{\bullet })& \text{si }p=0\\ \text{im }{H}^{q+1}{f}^{\bullet }:H^{q+1}(A^{\bullet })\to H^{q+1}(B^{\bullet })& \text{si }p=1\end{array}$

Mais nous avons aussi une description directe du terme E₂ comme homologie du terme E₁. Ces deux descriptions doivent être isomorphes :

$H^q(B^{\bullet })/H^q(A^{\bullet })\cong \ker d_{0,q}^1:H^q(C^{\bullet })\to H^{q+1}(A^{\bullet })$

$\text{im }{H}^{q+1}{f}^{\bullet }:H^{q+1}(A^{\bullet })\to H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/(\text{im }{d}_{0,q}^1:H^q(C^{\bullet })\to H^{q+1}(A^{\bullet }))$

Le premier donne l'exactitude en C, et le second en les groupes de cohomologie en A.

Suite spectrale d'un complexe bigradué

On trouve pour un complexe bigradué que :

$H_p^I(H_q^{II}(C_{\bullet ,\bullet })){\Rightarrow }_p{H}^{p+q}(T(C_{\bullet ,\bullet }))$

$H_q^{II}(H_p^I(C_{\bullet ,\bullet })){\Rightarrow }_q{H}^{p+q}(T(C_{\bullet ,\bullet }))$

Remarquer qu'en général, les deux filtrations sur H^p+q(T(C_•,•)) sont distinctes.

Exemples

Pages en premier quadrant

Soit une suite spectrale où $E_r^{p,q}$ s'annule pour tout $p$ et $q$ négatif, dit suite spectrale en premier quadrant. La suite aboutie car on a $E_{r+i}^{p,q}=E_r^{p,q}$ pour tout $i\ge 0$ si $r>p$ et $r>q+1$.

Deux colonnes adjacentes

Soit $E_{p,q}^r$ une suite spectrale homologique telles que $E_{p,q}^2=0$ pour tout p autre que 0, 1. Visuellement, la deuxième page $E^2$ est :

$\begin{array}{cccccc}& ⋮& ⋮& ⋮& ⋮& \\ \cdots & 0& E_{0,2}^2& E_{1,2}^2& 0& \cdots \\ \cdots & 0& E_{0,1}^2& E_{1,1}^2& 0& \cdots \\ \cdots & 0& E_{0,0}^2& E_{1,0}^2& 0& \cdots \\ \cdots & 0& E_{0,-1}^2& E_{1,-1}^2& 0& \cdots \\ & ⋮& ⋮& ⋮& ⋮& \end{array}$

Les différentielles en seconde page ont bidegrée (-2, 1), donc s'écrivent

$d_{p,q}^2:E_{p,q}^2\to E_{p-2,q+1}^2$

Ces applications sont toutes nulles car

$d_{0,q}^2:E_{0,q}^2\to 0$, $d_{1,q}^2:E_{1,q}^2\to 0$

ainsi la suite spectrale dégénère : $E^{\mathrm{\infty }}=E^2$. Elle converge vers, disons, $H_{*}$ avec une filtration

$0=F_{-1}{H}_n\subset F_0{H}_n\subset \dots \subset F_n{H}_n=H_n$

telle que $E_{p,q}^{\mathrm{\infty }}=F_p{H}_{p+q}/F_{p-1}{H}_{p+q}$. Alors $F_0{H}_n=E_{0,n}^2$, $F_1{H}_n/F_0{H}_n=E_{1,n-1}^2$, $F_2{H}_n/F_1{H}_n=0$, $F_3{H}_n/F_2{H}_n=0$, etc. On a donc une suite exacte courte :

$0\to E_{0,n}^2\to H_n\to E_{1,n-1}^2\to 0$.

Deux lignes adjacentes

De même, on considère $E_{p,q}^r$ une suite spectrale concentrée en page deux sur les lignes q = 0, 1. Contrairement au cas précédent, elle ne dégénère pas nécessairement en page deux, mais sûrement en page trois.

Supposons que la suite converge vers H avec une filtration F comme dans l'exemple précédent. Puisque $F_{p-2}{H}_p/F_{p-3}{H}_p=E_{p-2,2}^{\mathrm{\infty }}=0$, $F_{p-3}{H}_p/F_{p-4}{H}_p=0$, etc., on a: $0\to E_{p-1,1}^{\mathrm{\infty }}\to H_p\to E_{p,0}^{\mathrm{\infty }}\to 0$, et finalement :

$\cdots \to H_{p+1}\to E_{p+1,0}^2\stackrel{d}{\to }{E}_{p-1,1}^2\to H_p\to E_{p,0}^2\stackrel{d}{\to }{E}_{p-2,1}^2\to H_{p-1}\to \dots .$

Suite de Wang

Le calcul de la section précédente se généralise de manière simple. Considérons une fibration sur une sphère :

$F\stackrel{i}{\to }E\stackrel{p}{\to }{S}^n$

avec n supérieur ou égal à 2. Nous avons la suite spectrale de Serre :

$E_{p,q}^2=H_p(S^n;H_q(F))\Rightarrow H_{p+q}(E)$;

C'est-à-dire que $E_{p,q}^{\mathrm{\infty }}=F_p{H}_{p+q}(E)/F_{p-1}{H}_{p+q}(E)$ avec une filtration $F_{\bullet }$.

On sait que $H_p(S^n)$ est non nulle si p ou n vaut zéro et vaut Z dans ce cas, on voit que $E_{p,q}^2$ consiste en seulement deux lignes $p=0,n$, Ainsi la page en $E^2$ est donnée par

$\begin{array}{ccccccccc}& ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮& \\ \cdots & 0& E_{0,2}^2& 0& \cdots & 0& E_{n,2}^2& 0& \cdots \\ \cdots & 0& E_{0,1}^2& 0& \cdots & 0& E_{n,1}^2& 0& \cdots \\ \cdots & 0& E_{0,0}^2& 0& \cdots & 0& E_{n,0}^2& 0& \cdots \end{array}$

De plus, sachant

$E_{p,q}^2=H_p(S^n;H_q(F))=H_q(F)$

pour $p=0,n$ par le théorème des coefficients universels, $E^2$ s'illustre comme suit :

$\begin{array}{ccccccccc}& ⋮& ⋮& ⋮& & ⋮& ⋮& ⋮& \\ \cdots & 0& H_2(F)& 0& \cdots & 0& H_2(F)& 0& \cdots \\ \cdots & 0& H_1(F)& 0& \cdots & 0& H_1(F)& 0& \cdots \\ \cdots & 0& H_0(F)& 0& \cdots & 0& H_0(F)& 0& \cdots \end{array}$

La seule différentielle non nulle en page $E^n$ est donnée par

$d_{n,q}^n:E_{n,q}^n\to E_{0,q+n-1}^n$

qui est

$d_{n,q}^n:H_q(F)\to H_{q+n-1}(F)$

La suite spectrale converge en page $E^{n+1}=E^{\mathrm{\infty }}$. On en déduit une suite exacte

$0\to E_{n,q-n}^{\mathrm{\infty }}\to E_{n,q-n}^n\stackrel{d}{\to }{E}_{0,q-1}^n\to E_{0,q-1}^{\mathrm{\infty }}\to 0.$

c'est-à-dire :

$0\to E_{n,q-n}^{\mathrm{\infty }}\to H_{q-n}(F)\stackrel{d}{\to }{H}_{q-1}(F)\to E_{0,q-1}^{\mathrm{\infty }}\to 0.$

Pour expliciter les termes en $E^{\mathrm{\infty }}$, notons $H=H(E)$. Puisque$F_1{H}_q/F_0{H}_q=E_{1,q-1}^{\mathrm{\infty }}=0$, etc., on a: $E_{n,q-n}^{\mathrm{\infty }}=F_n{H}_q/F_0{H}_q$ et donc, avec $F_n{H}_q=H_q$,

$0\to E_{0,q}^{\mathrm{\infty }}\to H_q\to E_{n,q-n}^{\mathrm{\infty }}\to 0.$

D'où une suite exacte

$0\to H_q(F)\to H_q(E)\to H_{q-n}(F)\to 0.$

Ainsi, on en déduit avec tout cela la suite exacte longue :

$\dots \to H_q(F)\stackrel{i_{*}}{\to }{H}_q(E)\to H_{q-n}(F)\stackrel{d}{\to }{H}_{q-1}(F)\stackrel{i_{*}}{\to }{H}_{q-1}(E)\to H_{q-n-1}(F)\to \dots$

(La suite de Gysin est obtenue de manière similaire.)

Suites notoires

Quelques suites spectrales notoires :

Articles connexes

• Cohomologie
• Transgression

Notes et références

Références

• Modèle:Ouvrage
• Modèle:Ouvrage
• Modèle:Article
• Séminaire Henri Cartan de l'École Normale Supérieure, 1950/1951. Cohomologie des groupes, suite spectrale, faisceaux
• Modèle:Ouvrage
• Modèle:Ouvrage
• Modèle:En Robert Mosher et Martin Tangora, Cohomology Operations and Applications in Homotopy Theory
• Modèle:EnModèle:Ouvrage
• Modèle:En Modèle:Article
• Modèle:En Modèle:Article
• Modèle:Lien web
• Modèle:En Modèle:Ouvrage
• Modèle:En Modèle:Ouvrage
• Modèle:Ouvrage