Aiguille de Buffon

L'aiguille de Buffon est une expérience de probabilité proposée en 1733 par Georges-Louis Leclerc de Buffon, un scientifique français du Modèle:XVIIIe siècle. Cette expérience fournit une approximation du nombre [[Pi|Modèle:Math]]. Son analyse met en œuvre un cas simple d'espace de probabilités bidimensionnel et continu.

Procédé pratique

Représentation graphique de 10 essais de l'expérience.

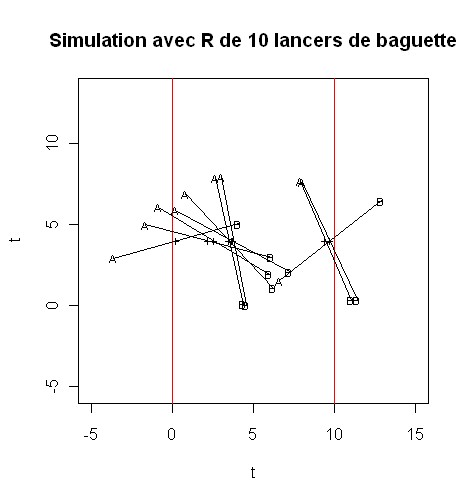
Il s'agit de lancer un grand nombre de fois une aiguille sur un parquet. Le parquet est composé de planches parallèles de même largeur. On comptabilise le nombre de fois où l'aiguille tombe à cheval sur [au moins] une rainure du parquet (cas "favorable") par rapport au nombre total de lancers. Au fur et à mesure que le nombre de lancers augmente, le quotient se rapproche d'un certain nombre permettant de retrouver Modèle:Math (par exemple, si la longueur de l'aiguille est égale à la largeur d'une planche, ce nombre sera Modèle:Math).

Conditions et hypothèses

Pour que l'expérience fonctionne correctement :

• les lancers successifs doivent être nombreux, indépendants, et on doit considérer une situation d'équiprobabilité (la position de l'aiguille est indifférente, en position et en angle, par rapport au parquet) ;
• tous les lancers doivent être reproduits dans des conditions identiques ;
• la longueur de l'aiguille doit être inférieure ou égale à la largeur d'une planche du parquet.

Étude mathématique

2 aiguilles de Buffon (noires) sur un parquet.

Soient :

• $l$ le réel positif correspondant à la largeur d'une latte de parquet ;
• a le réel positif correspondant à la longueur de l'aiguille ;
• Modèle:Math le réel compris entre 0 et Modèle:Frac correspondant à l'angle géométrique formé avec les rainures du parquet ;
• $r$ le réel positif correspondant à la distance du centre de l'aiguille à la rainure la plus proche.

D'après les hypothèses, et en utilisant toutes les symétries, on peut considérer que :

• Modèle:Math suit une loi uniforme continue sur $[0;\frac{\pi }{2}]$
• $r$ suit une loi uniforme continue sur $[0;\frac{l}{2}]$

Point de vue géométrique simple

Considérons n lancers (n assez grand) de cette aiguille. On peut considérer alors que toutes les positions différentes de l'aiguille mises bout à bout forment un polygone à $n$ côtés. Plus n est grand plus ce polygone se rapprochera d'un cercle. Le périmètre P de ce cercle vaut alors $P=n\times a$. Le diamètre de ce cercle vaudra $D=P/\pi =n\times a/\pi$. Le problème revient à savoir : combien de rainures parallèles sont coupées par le polygone, ou encore combien y a-t-il de rainures à l'intérieur du cercle ?

Le nombre d'intersections $i$ du cercle avec les rainures est donné par $i/2\times l=D$ ($i/2$ car le cercle est coupé à droite et à gauche); comme $n$ est grand le diamètre du cercle $D$ est grand par rapport à $l$. Finalement la probabilité que l'aiguille coupe une rainure est donnée par: Modèle:Retrait et en simplifiant: Modèle:Retrait

Cas limite

Considérons un lancer isolé. Si l'aiguille touche un point de la rainure avec sa pointe sans la chevaucher, alors on a un triangle rectangle dont l'hypoténuse est la moitié de l'aiguille, un côté est la longueur r, l'autre côté une portion de la rainure. On a alors :

$\sin \theta =\frac{r}{\frac{a}{2}}\iff \frac{a}{2}\sin \theta =r$

Cas défavorable

Par conséquent, si l'aiguille est pleinement sur une planche, on aura :

$\frac{a}{2}\sin \theta <r$

Cas favorable

Si elle chevauche au moins une rainure (la plus proche), on aura :

$\frac{a}{2}\sin \theta >r$

Analyse

Pour a égale ou plus petit que l

On traite ici du cas où l'aiguille est de même longueur ou plus courte que l'écart entre les lames du parquet.

De même que, pour les probabilités discrètes, on forme le quotient des cas "favorables" aux cas "totaux", on aura dans $[0;\frac{\pi }{2}]$ x $[0;\frac{a}{2}\sin \theta ]$ la probabilité pour une aiguille de tomber sur une rainure l'expression :

$\frac{{\text{Aire}}_{\text{favorable}}}{{\text{Aire}}_{\text{totale}}}$

Soit (dessiner l'espace $(r,\theta )$ et la limite) :

$P\left(\text{favorable}\right)=\frac{1}{\frac{\pi }{2}\frac{l}{2}}\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(\underset{0}{\overset{\frac{a}{2}\sin \theta }{\int }}\mathrm{d}r\right)\mathrm{d}\theta =\frac{4}{\pi l}\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{a}{2}\sin \theta \mathrm{d}\theta =\frac{2a}{\pi l}$

Après une multitude de lancers, d'après la loi des grands nombres, la valeur pratique tendra à se rapprocher de la valeur théorique $\frac{2a}{\pi l}$. On peut alors facilement retrouver [[pi|Modèle:Math]] en connaissant les données de l'expérience (l et a).

En effet, soit p la proportion qui estime P : alors on a un estimateur pour $\pi \simeq \frac{2a}{lp}.$

Pour a plus grand que l

On traite ici du cas où l'aiguille est plus longue que l'écart entre les lames du parquet. Le cas « favorable » est encore : « l'aiguille croise [au moins] une lame de parquet ».

Le cas « défavorable » étant plus facile à exprimer mathématiquement, on a (dessiner l'espace $(r,\theta )$ et la limite) :

$P=1-\frac{1}{\frac{\pi l}{4}}\underset{0}{\overset{\arcsin (\frac{l}{a})}{\int }}\left(\underset{\frac{a}{2}\sin \theta }{\overset{\frac{l}{2}}{\int }}\mathrm{d}x\right)\mathrm{d}\theta$ $P=\frac{2a}{\pi l}(1-\sqrt{1-\frac{l^2}{a^2}})+(1-\frac{2\arcsin \frac{l}{a}}{\pi })$

On confirme que pour $l=a$, on retrouve la formule précédente (établie pour $l⩾a$ : une aiguille courte).

La formule permet encore d'estimer $\pi$ en fonction de $(1-p)$ où $p$ est la proportion qui estime $P$ puisque $(1-P)$ a $\pi$ en facteur.

En posant $\frac{l}{a}=u$ et en développant au voisinage de $u=0$, on trouve l'expression de la probabilité pour une très longue aiguille (formule approchée) :

$P_{a>>l}=1-\frac{l}{\pi a}$

qui tend vers 1 pour a très grand, comme on l'espérait.

Voir aussi

Articles connexes

• Méthode de Monte-Carlo

Bibliographie

Martin Aigner et Günter M. Ziegler (trad. Nicolas Puech), Raisonnements divins : quelques démonstrations mathématiques particulièrement élégantes, Springer Verlag, Modèle:2e éd., 2006, 270 p. Modèle:ISBN

Liens externes

• Un applet Java qui permet de simuler l'expérience de l'aiguille de Buffon
• Un site qui mentionne le fait qu'une expérience de probabilité censée produire un quotient (dans Q) amène $\pi$ (dans R)
• Une expérience numérique interactive en Javascript de l'aiguille de Buffon sur experiences.math.cnrs.fr
• Un simulateur Monte-Carlo open source sous MATLAB proposant l'exemple de l'aiguille de Buffon