Étendue géométrique

L'étendue géométrique et l'étendue optique sont deux grandeurs, utilisées en radiométrie et en photométrie, qui caractérisent la part du rayonnement lumineux émis par une source étendue qui atteint un récepteur. Leur unité dans le système international est le mètre carré-stéradian (mModèle:Exp·sr).

Le faisceau est l'ensemble des rayons reliant l'un quelconque des points de la surface émettrice à l'un quelconque des points de la surface réceptrice. L'étendue géométrique peut être vue comme la grandeur géométrique caractérisant la taille de ce canal, ou de ce tube, de transfert. Elle peut aussi bien être définie du point de vue du récepteur que de la source. L'étendue géométrique permet de relier deux grandeurs photométriques ou radiométriques, d'une part le flux lumineux ${\mathrm{\Phi }}_v$ et la luminance lumineuse $L_v$, et d'autre part le flux énergétique ${\mathrm{\Phi }}_e$ et la luminance énergétique $L_e$.

L'étendue optique, quant à elle, permet de prendre en compte les variations de l'indice de réfraction du milieu au cours de la propagation : cette dernière influence la dispersion des rayons lumineux. La conservation de l'étendue d'un faisceau au travers d'un système optique exprime la conservation de la puissance lumineuse de ce faisceau, et donc l'absence de perte dans le système. La notion est reliée à celle d'invariant de Lagrange-Helmholtz, également constant dans un système optique parfait. C'est un concept fondamental en optique non imageante.

Définitions

Fichier:Notation Etendue geometrique.svg

Notations utilisées.

Étendue géométrique élémentaire

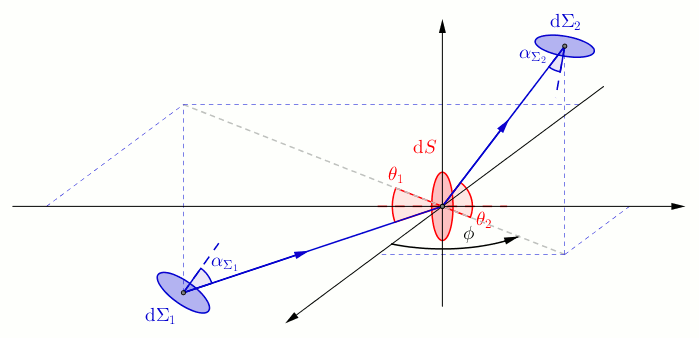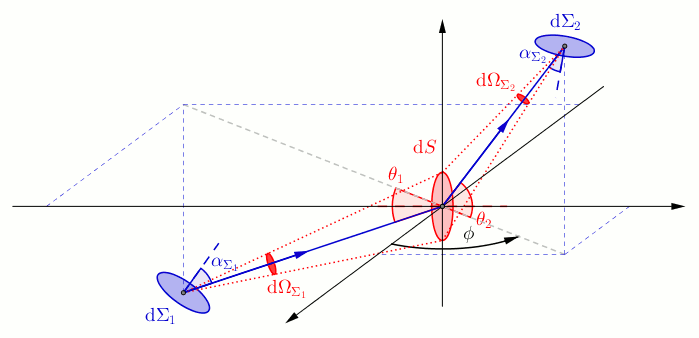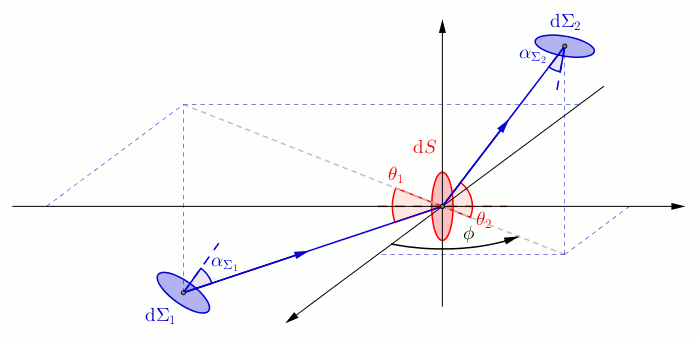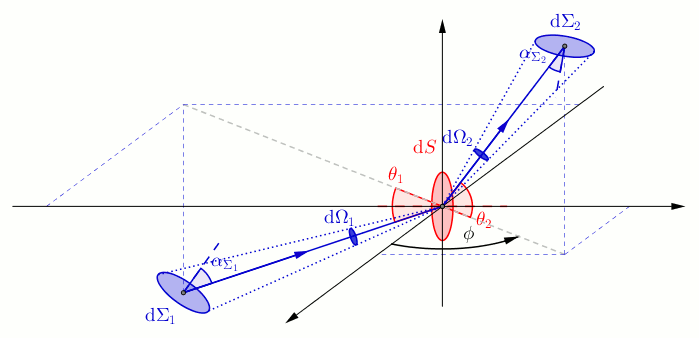
Considérons une source lumineuse $\mathrm{\Sigma }$ et un récepteur $S$, tous deux étendus, c'est-à-dire constitués d'un ensemble de points, séparés par un milieu parfaitement transparent. Pour étudier la transmission de la lumière entre ces deux surfaces il faut étudier la contribution de chaque point de $\mathrm{\Sigma }$ à l'éclairement de chaque point de $S$. On fait appel au calcul infinitésimal, ainsi l'étendue géométrique d'un élément de surface $\mathrm{d}\mathrm{\Sigma }$ vers un élément de surface $\mathrm{d}S$ s'exprimeModèle:, :

${\mathrm{d}}^{2}G=\mathrm{d}\mathrm{\Sigma }\cos {\alpha }_{\mathrm{\Sigma }}\mathrm{d}{\mathrm{\Omega }}_{\mathrm{\Sigma }}=\frac{\mathrm{d}\mathrm{\Sigma }\cos {\alpha }_{\mathrm{\Sigma }}\mathrm{d}S\cos {\alpha }_S}{d^2}$.

• $\mathrm{d}\mathrm{\Sigma }$ et $\mathrm{d}S$ sont deux éléments de surface suffisamment petits pour qu'on puisse les assimiler à des portions de plan, appartenant respectivement à $\mathrm{\Sigma }$ et $S$ et reliés par un faisceau lumineux élémentaire.
• ${\overrightarrow{n}}_{\mathrm{\Sigma }}$ et ${\overrightarrow{n}}_S$ sont respectivement les vecteurs normaux unitaires des éléments de surface $\mathrm{d}\mathrm{\Sigma }$ et $\mathrm{d}S$.
• ${\alpha }_{\mathrm{\Sigma }}$ et ${\alpha }_S$ sont les angles entre la direction de propagation et vecteur normal correspondant, respectivement ${\overrightarrow{n}}_{\mathrm{\Sigma }}$ et ${\overrightarrow{n}}_S$.
• $\mathrm{d}{\mathrm{\Omega }}_{\mathrm{\Sigma }}$ est l'angle solide sous lequel l'élément de surface $\mathrm{d}S$ est vu depuis l'élément de surface $\mathrm{d}\mathrm{\Sigma }$, par définition : $\mathrm{d}{\mathrm{\Omega }}_{\mathrm{\Sigma }}=\mathrm{d}S\cos {\alpha }_S/d^2$.
• $d$ la distance des deux surfaces élémentaires $\mathrm{d}\mathrm{\Sigma }$ et $\mathrm{d}S$.

Il est intéressant d'observer la propriété suivante : l'étendue géométrique de $\mathrm{d}\mathrm{\Sigma }$ vers $\mathrm{d}S$ est égale à l'étendue géométrique de $\mathrm{d}S$ vers $\mathrm{d}\mathrm{\Sigma }$. En effet, le canal qui relie les deux surfaces est le même.

Étendue géométrique intégrale

L'étendue géométrique, parfois qualifiée de totale, globale ou intégrale, qui relie les surfaces $\mathrm{\Sigma }$ et $S$ est l'intégrale double sur $\mathrm{d}\mathrm{\Sigma }$ et $\mathrm{d}S$ de l'étendue élémentaire, sur les parties des deux surfaces $\mathrm{\Sigma }$ et $S$ qui sont visibles de l'une à l'autre. L'étendue du système dans son ensemble est donc :

$G=\underset{\mathrm{\Sigma }}{\int }\underset{S}{\int }{\mathrm{d}}^{\mathrm{2}}G.$

Ici encore, l'étendue géométrique du faisceau qui relie $\mathrm{\Sigma }$ et $S$ est la même suivant que l'on considère le faisceau élémentaire au départ ou à l'arrivée.

Étendue optique élémentaire

Tout au long de la propagation du faisceau lumineux l'étendue géométrique peut changer : une ou plusieurs réflexions ou réfractions peuvent le dévier et modifier sa géométrie. L'étendue optique permet de prendre en compte les variations de l'indice de réfraction. Son expression est :

${\mathrm{d}}^{2}O=n^2{\mathrm{d}}^{2}G$.

L'étendue optique élémentaire est un invariant optique : $n^2{\mathrm{d}}^{2}G$ se conserve dans les réflexions et les réfractions.

Fichier:Etendue optique conservation.gif

Notations utilisées.

La loi de Snell-Descartes permet d'établir :

$n_1\sin {\theta }_1=n_2\sin {\theta }_2$,

puis en prenant la différentielle,

$n_1\cos {\theta }_1\mathrm{d}{\theta }_1=n_2\cos {\theta }_2\mathrm{d}{\theta }_2$.

Pour une variation d'angle d'incidence $d{\theta }_1$, l'angle réfracté varie de $d{\theta }_2$. En multipliant les deux relations précédentes, il vient

$n_1^2\cos {\theta }_1(\sin {\theta }_1\mathrm{d}{\theta }_1\mathrm{d}\varphi )=n_2^2\cos {\theta }_2(\sin {\theta }_2\mathrm{d}{\theta }_2\mathrm{d}\varphi ),$

où le tout a aussi été multiplié par $\mathrm{d}\varphi$ car l'angle $\varphi$ ne change pas lors de la réfraction, les deux rayons restent dans le même plan. On reconnait, entre parenthèses, l’expression de l'angle solide, aussi l'expression devient :

$n_1^2\cos {\theta }_1\mathrm{d}{\mathrm{\Omega }}_1=n_2^2\cos {\theta }_2\mathrm{d}{\mathrm{\Omega }}_2$.

Enfin, on multiplie par $\mathrm{d}S$ :

$n_1^2\mathrm{d}S\cos {\theta }_1\mathrm{d}{\mathrm{\Omega }}_1=n_2^2\mathrm{d}S\cos {\theta }_2\mathrm{d}{\mathrm{\Omega }}_2$,

c'est-à-dire

$n_1^2\mathrm{d}{G}_1=n_2^2\mathrm{d}{G}_2\iff \mathrm{d}{O}_1=\mathrm{d}{O}_2$.

Ceci montre que l'étendue optique de la lumière réfracté en $\mathrm{d}S$ se conserve. On pourrait obtenir le même résultat dans le cas de la réflexion avec $n_1=n_2$ et ${\theta }_1=-{\theta }_2$. Modèle:Démonstration/fin

Étendue optique intégrale

L'étendue du système dans son ensemble est donc :

$O=\underset{\mathrm{\Sigma }}{\int }\underset{S}{\int }{\mathrm{d}}^{\mathrm{2}}O=n^{2}G$.

On peut montrer que l'étendue optique $n^{2}G$ se conserve s'il est soumis à des phénomènes de réfraction et de réflexion. Elle est donc également conservée lorsque les rayons traversent un système optique parfait. Cette conservation peut se démontrer de différentes manières, à partir de l'optique hamiltonienne ou via la seconde loi de la thermodynamique. En revanche, l'étendue n'est pas conservée lorsque les rayons sont diffusés, ce qui conduit à augmenter l'angle solide du faisceau lumineux. Dans un système réel, l'étendue peut donc rester constante ou augmenter, mais ne peut pas diminuer. C'est une conséquence directe de l'augmentation de l'entropie du système, qui ne peut être compensée qu'en disposant d'une information a priori permettant de reconstituer un front d'onde cohérent, par conjugaison de phase.

Cohérence d'un faisceau lumineux

On prouve qu'un faisceau monochromatique de longueur d'onde $\lambda$ est cohérent sur une étendue géométrique proche de ${\lambda }^2$.

Facteur de forme

Modèle:Article détaillé Dans le cas usuel d'un rayonnement dans l'air, où $n=1$, l'étendue géométrique du faisceau lumineux élémentaire peut se mettre sous la forme :

${\mathrm{d}}^{2}G=\pi \mathrm{d}\mathrm{\Sigma }\left(\frac{\cos {\theta }_{\mathrm{\Sigma }}\cos {\theta }_S}{\pi d^2}\mathrm{d}S\right)$.

Le terme mis entre parenthèses est le facteur de forme élémentaire du transfert de $\mathrm{d}\mathrm{\Sigma }$ vers $\mathrm{d}S$.

Voir aussi

Liens externes

• Cours de rayonnement, Chapitre 3 : Mesure géométrique des faisceaux. Olivier Perrot (2010).