Empilement de sphères dans une sphère
Aller à la navigation
Aller à la recherche
Modèle:Voir homonymes L'empilement de sphères dans une sphère est un problème d'empilement tridimensionnel dont l'objectif est d'empiler des sphères identiques de nombre Modèle:Mvar dans une sphère unité. C’est l’équivalent tridimensionnel du problème bidimensionnel de l'empilement de cercles dans un cercle.
| Nombre de sphères unités Modèle:Mvar | Rayon maximal des sphères intérieures[1] | Optimalité | Figure | |
|---|---|---|---|---|
| Forme exacte | Approximation | |||
| 1 | 1,0000 | Trivial | 
| |
| 2 | 0,5000 | Trivial | 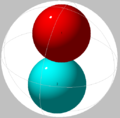
| |
| 3 | 0,4641... | Trivial | 
| |
| 4 | 0,4494... | Prouvé optimal | 
| |
| 5 | 0,4142... | Prouvé optimal | 
| |
| 6 | 0,4142... | Prouvé optimal | 
| |
| 7 | 0,3859... | Prouvé optimal | 
| |
| 8 | 0,3780... | Prouvé optimal | 
| |
| 9 | 0,3660... | Prouvé optimal | 
| |
| 10 | 0,3530... | Prouvé optimal | 
| |
| 11 | 0,3445... | Prouvé optimal | 
| |
| 12 | 0,3445... | Prouvé optimal | 
| |