Formulaire des poutres simples

Modèle:À recycler Modèle:À sourcer Liste de formules de flexion pour des poutres dans différentes situations^[1]Modèle:,^[2].

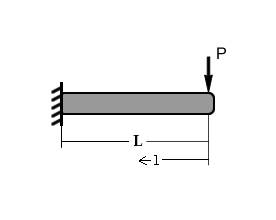
Poutre encastrée - libre

Le point $A$ est à gauche, le point $B$ est à droite, $P$ est la charge ponctuelle.

$E$ désigne le module de Young, $I$ désigne le moment quadratique.

Les indices, le sens des efforts et le sens des déformations sont omis lorsqu'il n'y a pas d'ambiguïté.

Une barre horizontale indique que la solution est indiquée ailleurs.

Sollicitation	Réaction d'appui	Flèche	Rotation	Équation de la déformée
	$R_{A} = P$ $M_{A} = P L$	$f = \frac{P L^{3}}{3 E I}$	$ϕ = \frac{P L^{2}}{2 E I}$	$y = \frac{P x^{2}}{6 E I} (3 L - x)$
	$R_{A} = w L$ $M_{A} = \frac{w L^{2}}{2}$	$f = \frac{w L^{4}}{8 E I}$	$ϕ = \frac{w L^{3}}{6 E I}$	$y = \frac{- w x^{2}}{24 E I} (x^{2} - 4 L x + 6 L^{2})$

Réaction d'appui	Flèche	Rotation	Moment	Équation de la déformée
$R_{A} = \frac{M_{O}}{L}$ $R_{B} = - \frac{M_{O}}{L}$	$f = \frac{M_{0} L}{8 E I}$	$ϕ_{A} = \frac{M_{0} L}{3 E I}$ $ϕ_{B} = \frac{M_{0} L}{6 E I}$	-	$y = \frac{- M_{0} x}{6 E I L} (x^{2} - 3 L x + 2 L^{2})$
$R_{A} = \frac{P b}{L}$ $R_{B} = \frac{P a}{L}$	$f_{P} = \frac{P a^{2} b^{2}}{3 E I L}$ $f_{m a x; a > L / 2} = \frac{P b}{27 E I L} \sqrt{3 (L^{2} - b^{2})^{3}}$ $x_{f m a x} = \frac{\sqrt{3 (L^{2} - b^{2})}}{3}$	$ϕ_{A} = \frac{P a b (2 L - a)}{6 E I L}$ $ϕ_{B} = \frac{P a b (L + a)}{6 E I L}$	$M = \frac{P a b}{L}$	$y (x < a) = \frac{- P b x}{6 E I L} (L^{2} - b^{2} - x^{2})$ $y (x > a) = \frac{P a}{6 E I L} ((L - x)^{3} - (L - a) (L + a) (L - x))$
$R_{A} = \frac{P}{2}$ $R_{B} = \frac{P}{2}$	$f = \frac{P L^{3}}{48 E I}$	$ϕ_{A} = \frac{P L^{2}}{16 E I}$ $ϕ_{B} = \frac{P L^{2}}{16 E I}$	$M = \frac{P L}{4}$	$y (x < \frac{L}{2}) = \frac{- P x}{48 E I} (3 L^{2} - 4 x^{2})$ $y (x > \frac{L}{2}) = \frac{P}{48 E I} (L^{3} - 9 x L^{2} + 12 x^{2} L - 4 x^{3})$