Généralités sur les machines électriques
Le but de cette page est d'expliquer et de démontrer comment une machine électrique fonctionne et produit un couple.
Circuit statique
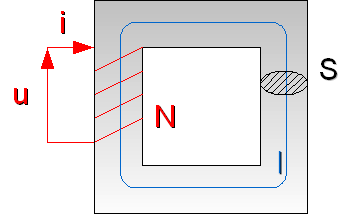
Soit un circuit magnétique entouré par un bobinage comportant N spires alimenté par une tension . On note le flux par spire et le flux total embrassé par la bobine.
On peut faire le schéma électrique équivalent suivant  avec une résistance R qui symbolise les pertes dans les câbles et une fem voir Loi de Lenz.
avec une résistance R qui symbolise les pertes dans les câbles et une fem voir Loi de Lenz.
donc on peut écrire :
En multipliant cette équation par on obtient :
Bilan des énergies

Donc on alimente un circuit magnétique avec une tension u, le circuit consomme une puissance We, on obtient de la chaleur W_th (les câbles chauffent) et le reste est de l'énergie magnétique. donc
Reprenons la formule plus haut On peut identifier la puissance consommée et les pertes thermiques.
Par identification on en déduit que . Donc :
Si on considère que le circuit est indéformable alors avec = surface délimitée par le circuit.
donc on en déduit avec Volume
donc
Cas linéaire : On considère que le matériau est non saturé.
donc et
si alors
on pose avec :
- = énergie magnétique
- = co-énergie
dans le cas linéaire =
Circuit déformable ou dynamique
Comme le circuit est en mouvement, on a de l'énergie mécanique en plus de l'énergie thermique et l'énergie magnétique.
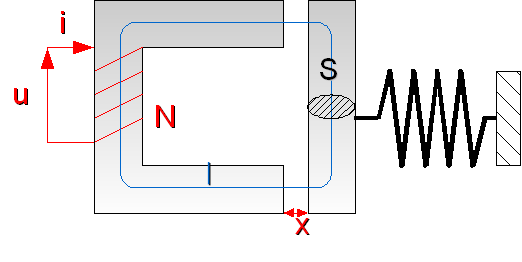
Donc : , avec :
- (déplacement linéaire) ou (rotation)
De plus on néglige les pertes fer et les frottements.
donc on obtient :
comme