Graphe partitionnable

En théorie des graphes, un graphe partitionnableModèle:, est un type particulier de graphe.

Définitions

Partition d'un entier

Soit $n$ un entier strictement positif, une partition de $n$ est une suite d’entiers $(s_1,\dots ,s_m)$ telle que :

• $m\ge 1$
• $\mathrm{\forall }i\in \{1,...,m\},s_i>0$
• $s_1+\dots +s_m=n$

Modèle:Math-partition d'un entier

Une $k$-partition de $n$ est une partition de $n$ possédant $k$ éléments.

Modèle:Math-partition d'un graphe

Soit $G=(V,E)$ un graphe simple où :

• $V$ est l'ensemble non vide des sommets de G.
• $E$ est l'ensemble des arêtes de G, c'est-à-dire un sous-ensemble de l'ensemble des parties à deux éléments de $V$.

Soit $S=(s_1,\dots ,s_m)$ une partition de $|V|$ (le nombre de sommets du graphe G).

$G$ est dit admettre une $S$-partition s'il existe une partition $P(S)=\{V_i:i\in \{1,...,m\}\}$ de $V$ telle que :

• $\mathrm{\forall }i\in \{1,...,m\},|V_i|=s_i$
• $\mathrm{\forall }i\in \{1,...,m\},G[V_i]$ est un graphe connexe.

L'ensemble $P(S)$ est alors dit être une partition de $G$ induite par $S$.

Graphe partitionnable

Un graphe $G=(V,E)$ est dit partitionnable s'il admet une $S$-partition pour toute partition $S$ de $|V|$.

Graphe Modèle:Math-partitionnable

Un graphe $G$ est dit $k$-partitionnable s'il admet une $S$-partition pour toute $k$-partition $S$ de $|V|$.

Exemples

Modèle:Math-partition de Modèle:Math

• Une $2$-partition de $5$ est $(3,2)$.
• Une $4$-partition de $10$ est $(1,4,1,4)$.
• Une $7$-partition de $22$ est $(2,2,3,1,3,8,3)$.

Modèle:Math-partition de Modèle:Math

Soit le graphe $G=(V,E)$ tel que :

• $V=\{a,b,c,d,e,f\}$
• $E=\{\{a,b\},\{b,c\},\{c,d\},\{d,e\},\{e,f\},\{f,a\},\{c,e\}\}$

représenté ci-dessous par :

$|V|=6$. $G$ admet 3 partitions de 6 possibles : $(1,1,4)$, $(1,2,3)$ et $(2,2,2)$ (en considérant que l'ordre des différentes suites n'a pas d'importance).

Ces trois partitions de l'entier 6 peuvent être appliquées respectivement pour partager le graphe $G$ comme ceci :

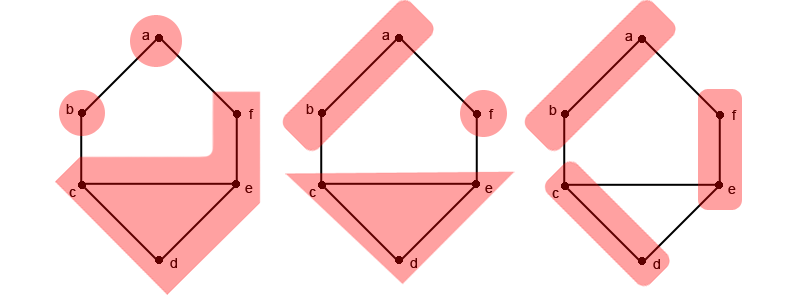
Il existe bien d'autres façons d'appliquer ces 3 partitions sur ce graphe. Le schéma ci-dessus est une des représentations possibles.