Graphe transposé

Un graphe et son transposé.

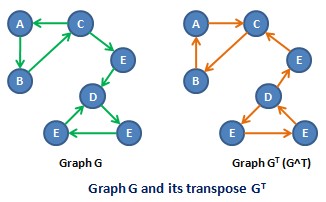
En théorie des graphes, le graphe transposé $G^T$, ou graphe inverse, d'un graphe orienté $G=(V,A)$ est obtenu en conservant tous les nœuds de $V$et en inversant tous les arcs de $A$. Autrement dit, $G^T=(V,A^T)$ avec $A^T=\{(y,x)\mid (x,y)\in A\}$.

Cette notion ne doit pas être confondue avec celle de graphe complémentaire ou inversé, pour les graphes non-orientés.

Propriétés

• Le transposé du transposé d'un graphe $G$ est le graphe $G$ .
• La matrice d'incidence du graphe transposé est la transposée de la matrice d'incidence du graphe original. Un graphe égal à son transposé est dit symétrique.

Applications

Certains algorithmes utilisent le transposé du graphe d'entrée, par exemple l'algorithme de Kosaraju effectue un parcours en profondeur du graphe et de son transposé.

Voir aussi

• Automate transposé, la notion analogue pour les automates finis.
• Relation binaire réciproque