Harmonique sphérique

Modèle:À vérifier En mathématiques, les harmoniques sphériques sont des fonctions harmoniques particulières, c'est-à-dire des fonctions dont le laplacien est nul. Les harmoniques sphériques sont particulièrement utiles pour résoudre des problèmes invariants par rotation, car elles sont les vecteurs propres de certains opérateurs liés aux rotations.

Les polynômes harmoniques Modèle:Math de degré Modèle:Mvar forment un espace vectoriel de dimension Modèle:Math, et peuvent s'exprimer en coordonnées sphériques Modèle:Math comme des combinaisons linéaires des (Modèle:Math) fonctions :

$r^l{Y}_{l,m}(\theta ,\phi )$,  avec $-l\le m\le +l$.

Les coordonnées sphériques Modèle:Math sont, respectivement, la distance au centre de la sphère, la colatitude et la longitude.

Tout polynôme homogène est entièrement déterminé par sa restriction à la sphère unité Modèle:Math.

C'est pourquoi la partie radiale de l'équation de Laplace, différente selon le problème étudié n'apparaît pas ici.

Les harmoniques sphériques sont utilisées en physique mathématique, dès qu'intervient la notion d'orientation (anisotropie) et donc de rotation (groupe de symétrie orthogonal Modèle:Math) et que le laplacien entre en jeu :

• en acoustique (reconstitution de l'effet d'espace par plusieurs haut-parleurs) ;
• en théorie du potentiel newtonien (électrostatique, mécanique, gravimétrie) ;
• en géophysique (représentation du globe terrestre, météorologie, champ magnétique terrestre) ;
• en cristallographie pour la texture ;
• en physique quantique (développement d'une fonction d'onde, densité du nuage électronique, description des orbitales atomiques de l'atome d'hydrogène) ;
• en cosmologie (représentation du ciel, en particulier pour l'analyse du fond diffus cosmologique)Modèle:Etc.

Elles sont également utilisées pour des problématiques de rendu 3D, notamment en réalité augmentée afin d'encoder des données d'éclairage ambiant.

Résolution de l'équation de Laplace

On cherche les fonctions Modèle:Math sous la forme d'un produit de deux fonctions d'une seule variable :

$Y_{l,m}(\theta ,\phi )=k{P}_{l,m}(\cos \theta ){\mathrm{e}}^{+im\phi }$

où Modèle:Mvar est une constante, qui sera fixée ultérieurement par la normalisation. L'équation aux valeurs propres devient une équation différentielle linéaire d'ordre deux pour la fonction Modèle:Math :

$-\frac{1}{\sin \theta }\frac{\mathrm{d}}{\mathrm{d}\theta }(\sin \theta \frac{\mathrm{d}{P}_{l,m}(\cos \theta )}{\mathrm{d}\theta })+\frac{m^2}{{\sin }^2\theta }{P}_{l,m}(\cos \theta )=E_{l,m}{P}_{l,m}(\cos \theta )$

Représentations des premières harmoniques sphériques "réelles" (combinaisons linéaires des $Y_{\ell ,m}$ de même $\ell$). Les parties en bleu correspondent aux valeurs négatives, celles en jaune aux valeurs positives des harmoniques.

On fait le changement de variable : $\theta \mapsto x=\cos \theta$ qui conduit à l'équation différentielle généralisée de Legendre :

$-\frac{\mathrm{d}}{\mathrm{d}x}[(1-x^2)\frac{\mathrm{d}{P}_{l,m}(x)}{\mathrm{d}x}]+\frac{m^2}{(1-x^2)}{P}_{l,m}(x)=E_{l,m}{P}_{l,m}(x)$

Les valeurs propres de cette équation sont indépendantes de Modèle:Mvar :

$E_{l,m}=l(l+1)$

Les fonctions propres Modèle:Math sont les polynômes associés de Legendre. Ils se construisent à partir des polynômes de Legendre Modèle:Math qui sont les fonctions propres de l'équation différentielle ordinaire de Legendre, correspondant au cas Modèle:Math :

$-\frac{\mathrm{d}}{\mathrm{d}x}[(1-x^2)\frac{\mathrm{d}{P}_l(x)}{\mathrm{d}x}]=l(l+1)P_l(x)$

On a la formule génératrice d'Olinde Rodrigues :

$P_l(x)=\frac{1}{2^{l}l!}\frac{{\mathrm{d}}^l}{\mathrm{d}{x}^l}{[x^2-1]}^l$

On construit alors les fonctions propres Modèle:Math par la formule :

$P_{l,m}(x)=(-1{)}^m{[1-x^2]}^{m/2}\frac{{\mathrm{d}}^m{P}_l(x)}{\mathrm{d}{x}^m}$

soit explicitement :

$P_{l,m}(x)=\frac{(-1{)}^m}{2^{l}l!}{[1-x^2]}^{m/2}\frac{{\mathrm{d}}^{l+m}}{\mathrm{d}{x}^{l+m}}{[x^2-1]}^l$

Remarque : il suffit en pratique de calculer les fonctions Modèle:Math pour Modèle:Math, car il existe une relation simple entre Modèle:Math et Modèle:Math :

$P_{l,-m}(x)=(-1{)}^m\frac{(l-m)!}{(l+m)!}{P}_{l,m}(x)$

Expression des harmoniques sphériques

On obtient alors l'expression inscrite plus bas. Une manière simple de retenir cette expression est la suivante :

$Y_{l,0}=P_l(\cos \theta )\cdot \sqrt{\frac{2l+1}{4\pi }}$,

où Modèle:Math est le polynôme de Legendre de degré Modèle:Mvar.

On obtient ensuite :

$J_{+}{Y}_{l,m}=\sqrt{(l^2-m^2)+(l-m)}\cdot Y_{l,m+1}$

où

$J_{+}={\mathrm{e}}^{\mathrm{i}\varphi }(\frac{\partial }{\partial \theta }+\frac{\mathrm{i}}{\tan \theta }\cdot \frac{\partial }{\partial \varphi })$

est l'opérateur « d'échelle montante ».

Pour Modèle:Mvar négatif, $Y_{l,m}=(-1{)}^m\cdot Y_{l,-m}^{*}$

Souvent cette base se note $|lm⟩$ :

toute fonction sur la sphère Modèle:Math pourra donc s'écrire :

$f(\theta ,\varphi )=f^{l,m}\cdot |lm⟩$

(en convention de sommation d'Einstein), les coefficients complexes Modèle:Math jouant le rôle de composantes de Modèle:Mvar dans la base des $|lm⟩$ (on dit parfois coefficients de Fourier généralisés).

En chimie ou en géophysique, il arrive qu'on préfère utiliser les harmoniques sphériques « réelles » et des coefficients de Fourier réels.

Expression mathématique

Les harmoniques sphériques formant une Modèle:Refsou orthogonale sur la sphère unité, Modèle:Refnec Modèle:Math Modèle:Précision nécessaire une série d'harmoniques sphériques :

$f(\theta ,\phi )=\sum _{l=0}^{+\mathrm{\infty }}\sum _{m=-l}^{+l}{C}_l^m\cdot Y_l^m(\theta ,\phi )$

où Modèle:Mvar et Modèle:Mvar sont des indices entiers, Modèle:Mvar est un coefficient constant et souvent en mathématiques prend le nom de coefficient de Fourier généralisé relativement à cette base.

Le développement en harmoniques sphériques est l'équivalent, appliqué aux fonctions angulaires, du développement en séries de Fourier pour les fonctions périodiques.

Modèle:Mvar est la partie réelle d'une fonction complexe Modèle:Mvar

$Y_l^m(\theta ,\phi )=\mathrm{Re}(\underset{\_}{Y_l^m}(\theta ,\phi ))$

Modèle:Mvar est appelée « fonction associée de Legendre » et est définie par

$\underset{\_}{Y_l^m}(\theta ,\phi )=\sqrt{\frac{2\cdot (l-m)!}{(l+m)!}}\cdot P_l^m(\cos \theta )\cdot {\mathrm{e}}^{\mathrm{i}m\phi }$

où Modèle:Math est l'imaginaire et Modèle:Mvar est le polynôme associé de Legendre :

$P_l^m(X)=\frac{(-1{)}^m}{2^l\cdot l!}\cdot (1-X^2{)}^{m/2}\cdot \frac{{\partial }^{m+l}}{\partial X^{m+l}}[(X^2-1{)}^l]$

On a donc

$Y_l^m(\theta ,\phi )=\sqrt{\frac{2\cdot (l-m)!}{(l+m)!}}\cdot P_l^m(\cos \theta )\cdot \cos (m\phi )$

On a par exemple :

• $P_0^0(\cos \theta )=1$ (Modèle:Math est isotrope) ;
• $P_1^0(\cos \theta )=\cos \theta$ ;
• $P_1^1(\cos \theta )=-\sin \theta$ ;
• $P_3^1(\cos \theta )=\frac{3}{2}\cdot \sin \theta \cdot (-5\cdot {\cos }^2\theta +1)$ ;

Les fonctions Modèle:Math présentent de plus en plus de symétries au fur et à mesure que Modèle:Mvar croît (sauf lorsque Modèle:Math, puisque Modèle:Math est une fonction constante et décrit donc une sphère).

Polynômes de Legendre

Pour les harmoniques circulaires, on utilise des polynômes Modèle:Mvar de la fonction cosinus :

$Y_l(\theta )=P_l(\cos \theta )$

Les polynômes Modèle:Mvar utilisés sont les polynômes de Legendre :

$P_l(X)=\frac{1}{2^l\cdot l!}\cdot \frac{d^l}{d{X}^l}[(X^2-1{)}^l]$ (formule de Rodrigues, mathématicien français)

On obtient :

• $P_0(\cos \theta )=1$ (fonction isotrope) ;
• $P_1(\cos \theta )=\cos \theta$ ;
• $P_2(\cos \theta )=\frac{1}{2}(3{\cos }^2\theta -1)$ ;
• $P_3(\cos \theta )=\frac{1}{2}(5{\cos }^3\theta -3\cos \theta )$ ;

Harmoniques sphériques normalisées

Base orthonormale des harmoniques sphériques

Parmi les Modèle:Math fonctions, l'habitude a été prise de sélectionner une base orthonormale sur la sphère ${𝕊}^2$ munie de la mesure

$\mathrm{d}\mu =\frac{1}{4\pi }\sin \theta \mathrm{d}\theta \mathrm{d}\varphi$,

soit le produit scalaire (hermitien en fait) :

$⟨f_1\mid f_2⟩=\frac{1}{4\pi }\underset{S^2}{\iint }{f}_1^{*}{f}_2\sin \theta \mathrm{d}\theta \mathrm{d}\varphi$

Les harmoniques sphériques sont les solutions de l'équation aux valeurs propres :

$-\mathrm{\Delta }{Y}_{l,m}(\theta ,\phi )=l(l+1)Y_{l,m}(\theta ,\phi )$

où l'opérateur laplacien s'écrit en coordonnées sphériques sur la sphère de rayon unité Modèle:Math :

$\mathrm{\Delta }f(\theta ,\phi )\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{J}^{2}f=\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }(\sin \theta \frac{\partial f}{\partial \theta })+\frac{1}{{\sin }^2\theta }\frac{{\partial }^{2}f}{\partial {\phi }^2}$

Elles sont fonctions propres de l'opérateur $J_3=-\mathrm{i}\frac{\partial }{\partial \varphi }$ :

$J_3{Y}_{l,m}=m\cdot Y_{l,m}$

Celles-ci, une fois normées sur la sphère sont alors notées usuellement Modèle:Math, où les angles Modèle:Math sont les coordonnées sphériques sur la sphère de rayon unité, et Modèle:Mvar et Modèle:Mvar sont deux nombres entiers tels que Modèle:Math et Modèle:Math

Normalisation

Les harmoniques sphériques constituent une base orthonormale de fonctions propres de l'opérateur laplacien sur la sphère de rayon unité Modèle:Math au sens où :

Elles sont orthogonales pour le produit scalaire suivant :

$\underset{S_2}{\iint }\mathrm{d}\mathrm{\Omega }(\theta ,\phi ){\bar{Y}}_{l^{\prime },m^{\prime }}(\theta ,\phi )Y_{l,m}(\theta ,\phi )={\delta }_{l,l^{\prime }}{\delta }_{m,m^{\prime }}$

Dans cette formule, Modèle:Math représente l'angle solide élémentaire :

$\mathrm{d}\mathrm{\Omega }(\theta ,\phi )=\sin \theta \mathrm{d}\theta \mathrm{d}\phi$

Toute fonction Modèle:Math suffisamment régulière admet un développement en série :

$f(\theta ,\phi )=\sum _{l=0}^{+\mathrm{\infty }}\sum _{m=-l}^{+l}{a}_{l,m}{Y}_{l,m}(\theta ,\phi )$

où les coefficients complexes Modèle:Math se calculent par :

$a_{l,m}=\underset{S_2}{\iint }\mathrm{d}\mathrm{\Omega }(\theta ,\phi ){\bar{Y}}_{l,m}(\theta ,\phi )f(\theta ,\phi )$

Expression des harmoniques sphériques normalisées

Les harmoniques sphériques généralisées sont définies sur la sphère Modèle:Math. La normalisation des harmoniques sphériques conduit à l'expression finale :

Forme « réelle » des harmoniques sphériques

Si Modèle:Mvar les harmoniques sphériques $Y_{\ell ,m}$ ont des valeurs complexes. Il est cependant possible, pour une valeur donnée de $\ell$ de définir des combinaisons linéaires des $Y_{\ell ,m}$ qui soient réelles, tout en constituant toujours une base normalisée sur la sphère unité.

Il suffit pour cela de prendre les combinaisons linéaires suivantes :

$\begin{array}{cc}{\tilde{Y}}_{\ell m}& =\{\begin{array}{cc}\frac{\mathrm{i}}{\sqrt{2}}(Y_{\ell }^m-(-1{)}^m{Y}_{\ell }^{-m})& \text{si}m<0,\\ Y_{\ell }^0& \text{si}m=0,\\ \frac{1}{\sqrt{2}}(Y_{\ell }^{-m}+(-1{)}^m{Y}_{\ell }^m)& \text{si}m>0.\end{array}\\ & =\{\begin{array}{cc}\frac{\mathrm{i}}{\sqrt{2}}(Y_{\ell }^{-|m|}-(-1{)}^m{Y}_{\ell }^{|m|})& \text{si}m<0,\\ Y_{\ell }^0& \text{si}m=0,\\ \frac{1}{\sqrt{2}}(Y_{\ell }^{-|m|}+(-1{)}^m{Y}_{\ell }^{|m|})& \text{si}m>0.\end{array}\\ \end{array}$

Il est facile de vérifier que ces expressions sont bien normalisées à l'unité. Ces relations s'inversent sans difficulté pour donner :

$Y_{\ell }^m=\{\begin{array}{cc}\frac{1}{\sqrt{2}}({\tilde{Y}}_{\ell |m|}-\mathrm{i}{\tilde{Y}}_{\ell ,-|m|})& \text{si}m<0,\\ {\tilde{Y}}_{\ell 0}& \text{si}m=0,\\ \frac{(-1{)}^m}{\sqrt{2}}({\tilde{Y}}_{\ell |m|}+\mathrm{i}{\tilde{Y}}_{\ell ,-|m|})& \text{si}m>0.\end{array}$

En substituant les expressions précédentes des harmoniques sphériques, on obtient les expressions générales suivantes :

${\tilde{Y}}_{\ell m}=\{\begin{array}{cc}\sqrt{2}\sqrt{\frac{(2\ell +1)}{4\pi }\frac{(\ell -|m|)!}{(\ell +|m|)!}}{P}_{\ell }^{|m|}(\cos \theta )\sin |m|\phi & \text{si }m<0,\\ \sqrt{\frac{(2\ell +1)}{4\pi }}{P}_{\ell }^0(\cos \theta )& \text{si }m=0,\\ \sqrt{2}\sqrt{\frac{(2\ell +1)}{4\pi }\frac{(\ell -m)!}{(\ell +m)!}}{P}_{\ell }^m(\cos \theta )\cos m\phi & \text{si }m>0.\end{array}$

Ces fonctions sont utilisées fréquemment en chimie quantique pour représenter les parties angulaires des différentes orbitales atomiques associées aux différents électrons du cortège électronique des atomes.

Représentations graphiques

Représentation sphérique

Si l'on utilise la représentation sphérique

$\rho ={\rho }_0+{\rho }_1\cdot Y_l^m(\theta ,\phi )$

alors la surface représentatrice est une sphère bosselée ; les bosses correspondent aux parties où Modèle:Mvar est positif, les creux aux parties où Modèle:Mvar est négatif. Lorsque Modèle:Mvar et Modèle:Mvar décrivent l'intervalle Modèle:Math, Modèle:Math s'annule selon Modèle:Mvar cercles :

• Modèle:Mvar cercles suivant un méridien, une iso-longitude (intersection entre un plan contenant Modèle:Mvar et la sphère) ;
• Modèle:Math cercles suivant un parallèle, une iso-latitude (intersection entre un plan parallèle à Modèle:Mvar et la sphère).

Le paramètre Modèle:Mvar est appelé le « degré », Modèle:Mvar est appelé l'« ordre azimutal ». Entre les cercles d'annulation, la fonction est alternativement positive ou négative.

Ci-dessous sont représentées quatre coupes de l'harmonique sphérique Modèle:Math :

Comme précédemment, on peut représenter la fonction par la courbe en coordonnées sphériques :

$Y_3^2$

$\rho ={\rho }_0+{\rho }_1\cdot Y_3^2(\theta ,\phi )$ les parties en blanc sont positives, en bleu négatives	$\rho =|Y_3^2(\theta ,\phi ){|}^2$

Représentation en coupe

Les harmoniques sphériques peuvent être représentées de façon plus simple sans les ventres de vibration, en ne gardant que les nœuds, comme le montre le tableau suivant. Ce sont les sphères de la figure du haut, projetées sur un plan vertical. On retrouve sur la dernière ligne les quatre sphères de la première figure ci-dessus où Modèle:Math. Les quatre valeurs de Modèle:Mvar y varient de 0 à 3 en valeur absolue. Sur la figure ci-après, on distingue les valeurs négatives pour tenir compte de ce que la rotation peut se faire dans un sens ou dans l'autre pour Modèle:Math. Pour montrer la concordance avec les harmoniques, leur plus simple expression est donnée sous chaque sphère.

On reconnaît les nombres quantiques secondaire Modèle:Mvar, correspondant aux sous-couches Modèle:Math, Modèle:Math, Modèle:Math, Modèle:Math et Modèle:Math, magnétique, de l'atome d'hydrogène. Le nombre quantique principal Modèle:Mvar n'apparaît pas car les modes radiaux sont différents selon le problème étudié, résonance acoustique, atome d'hydrogène ou autre.

Pour montrer la concordance avec la littérature, l’expression des harmoniques sphériques est donnée sous chaque sphère. Le nombre et la valeur des zéros des polynômes de Legendre associés, non normalisés, donne le nombre de parallèles et leur position sur l’axe vertical. L’exponentielle imaginaire Modèle:Math, de module unité, utilisée habituellement au lieu des sinus et cosinus, donne le nombre de méridiens. Les valeurs de Modèle:Math ne s’observent que dans les états excités ou les atomes de Rydberg où la valeur habituelle de Modèle:Mvar est 50 et dont l'orbitale est représentée non par une sphère mais par un anneau.

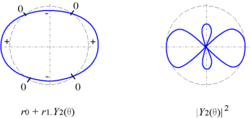
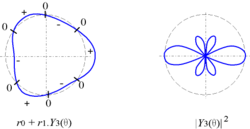
Représentation cartésienne et polaire

On peut représenter les harmoniques circulaires de trois manières :

• en coordonnées cartésiennes : Modèle:Math ;
• en coordonnées polaires : Modèle:Math
  avec Modèle:Math, utilisé par exemple pour un objet circulaire ; la courbe coupe le cercle de centre Modèle:Mvar et de rayon Modèle:Math lorsque la fonction s'annule ;
• en coordonnées polaires : Modèle:Math
  utilisé par exemple pour les fonctions d'onde en physique quantique.

Trois premières harmoniques circulaires

	Représentation cartésienne	Représentations polaires (tracé manuel)	Représentations polaires (tracé exact)
Modèle:Math
Modèle:Math
Modèle:Math

Autres harmoniques

Harmoniques circulaires

Dans le plan, la décomposition s'écrit :

$f(\theta )=\sum _{l=0}^{+\mathrm{\infty }}{C}_l\cdot Y_l(\theta )$

Modèle:Math est une fonction constante, la courbe représentatrice en coordonnées polaires Modèle:Math est donc un cercle de rayon Modèle:Math.

Modèle:Mvar est une fonction invariante par une rotation d'un angle de Modèle:Sfrac tour, c'est-à-dire que

$Y_l(\theta +\frac{2\pi }{l+1})=Y_l(\theta )$

on dit que Modèle:Mvar admet une symétrie d'ordre Modèle:Math.

Harmoniques sphériques généralisées

Lorsque l'on considère l'orientation d'un objet dans l'espace, il faut faire appel à trois angles ; on utilise en général les angles d'Euler Modèle:Math.

Considérons une fonction continue de l'orientation Modèle:Math ; comme précédemment, cette fonction peut être décomposée en harmoniques sphériques généralisées

$f(\psi ,\theta ,\phi )=\sum _{l=0}^{+\mathrm{\infty }}\sum _{m=-l}^{+l}\sum _{n=-l}^{+l}{C}_l^{mn}\cdot Y_l^{mn}(\psi ,\theta ,\phi )$

où Modèle:Mvar est une constante. La fonction Modèle:Mvar s'écrit :

$Y_l^{mn}(\psi ,\theta ,\phi )={\mathrm{e}}^{\mathrm{i}m\phi }\cdot P_l^{mn}(\cos \theta )\cdot {\mathrm{e}}^{\mathrm{i}n\psi }$

Le polynôme Modèle:Mvar est le polynôme de Legendre généralisé

$P_l^{mn}(X)=\frac{(-1{)}^{l-m}\cdot {\mathrm{i}}^{n-m}}{2^l\cdot (l-m)!}\cdot {\left[\frac{(l-m)!(l+n)!}{(l+m)!(l-n)!}\right]}^{1/2}\cdot (1-X{)}^{-\frac{n-m}{2}}$$\cdot (1+X{)}^{-\frac{n+m}{2}}\cdot \frac{{\partial }^{l-n}}{\partial X^{l-n}}[(1-X{)}^{l-m}(1+X{)}^{l+m}]$

Quand Modèle:Mvar décrit l'intervalle Modèle:Math, cette fonction Modèle:Mvar est soit réelle, soit imaginaire pure. Modèle:Math est la fonction isotrope (symétrie sphérique).

D'après la loi de composition des rotations, on a :

$Y_l^{mn}({\psi }_1+{\psi }_2,{\theta }_1+{\theta }_2,{\phi }_1+{\phi }_2)=\sum _{s=-l}^{+l}{Y}_l^{ms}({\psi }_1,{\theta }_1,{\phi }_1)\cdot Y_l^{sn}({\psi }_2,{\theta }_2,{\phi }_2)$

et en particulier

$P_l^{mn}(\cos ({\theta }_1+{\theta }_2))=\sum _{s=-l}^{+l}{P}_l^{ms}(\cos {\theta }_1)\cdot P_l^{sn}(\cos {\theta }_2)$

On a de manière générale :

$P_l^{mn}=P_l^{nm}=P_l^{-m-n}$

Par exemple pour Modèle:Math :

$P_1^{mn}(\cos \theta )$

Modèle:Mvar	Modèle:Mvar
	-1	0	+1
-1	$\frac{1}{2}(1+\cos \theta )$	$-\frac{\mathrm{i}}{\sqrt{2}}\sin \theta$	$\frac{1}{2}(\cos \theta -1)$
0	$-\frac{\mathrm{i}}{\sqrt{2}}\sin \theta$	$\cos \theta$	$-\frac{\mathrm{i}}{\sqrt{2}}\sin \theta$
1	$\frac{1}{2}(\cos \theta -1)$	$-\frac{\mathrm{i}}{\sqrt{2}}\sin \theta$	$\frac{\mathrm{i}}{2}(1+\cos \theta )$

Pour Modèle:Math :

$P_2^{mn}(\cos \theta )$

Modèle:Mvar	Modèle:Mvar
	-2	-1	0	+1	+2
-2	$\frac{1}{4}(\cos \theta +1{)}^2$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta +1)$	$-\frac{1}{2}\sqrt{\frac{3}{2}}(1-{\cos }^2\theta )$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta -1)$	$\frac{1}{4}(\cos \theta -1{)}^2$
-1	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta +1)$	$\frac{1}{2}(2{\cos }^2\theta +\cos \theta -1)$	$-\sqrt{\frac{3}{2}}\mathrm{i}\sin \theta \cos \theta$	$\frac{1}{2}(2{\cos }^2\theta -\cos \theta -1)$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta -1)$
0	$-\frac{1}{2}\sqrt{\frac{3}{2}}(1-{\cos }^2\theta )$	$-\sqrt{\frac{3}{2}}\mathrm{i}\sin \theta \cos \theta$	$\frac{1}{2}(3{\cos }^2\theta -1)$	$-\sqrt{\frac{3}{2}}\mathrm{i}\sin \theta \cos \theta$	$-\frac{1}{2}\sqrt{\frac{3}{2}}(1-{\cos }^2\theta )$
1	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta -1)$	$\frac{1}{2}(2{\cos }^2\theta -\cos \theta -1)$	$-\sqrt{\frac{3}{2}}i\sin \theta \cos \theta$	$\frac{1}{2}(2{\cos }^2\theta +\cos \theta -1)$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta +1)$
2	$\frac{1}{4}(\cos \theta -1{)}^2$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta -1)$	$-\frac{1}{2}\sqrt{\frac{3}{2}}(1-{\cos }^2\theta )$	$-\frac{\mathrm{i}}{2}\sin \theta (\cos \theta +1)$	$\frac{1}{4}(\cos \theta +1{)}^2$

Voir aussi

Articles connexes

• Équation de Laplace
• Atome
• Mécanique quantique
• Atome d'hydrogène
• Orbitale atomique, orbitale moléculaire
• Opérateur laplacien
• Polynôme de Legendre
• Géoïde
• Ambisonie
• Fonction spéciale

Liens externes

• Champs géophysiques, Modèle:Mvar. Vigny, cours de l'École normale supérieure
• La prévision numérique avec le modèle ARPEGE sur le site de Météo-France rubrique Comprendre la météo > Dossiers thématiques > La prévision numérique
• Simulateur d'harmoniques sphériques (programme JavaScript), site de l'École polytechnique (X), Palaiseau, France
• Spherical Harmonic, du site Eric Weisstein's World of Mathematics
• Oscillations propres de la Terre lors d'un séisme, une des applications des harmoniques sphériques (images gif animées) ;
• Représentations 3D de fonctions d'orientation
• Autour des harmoniques sphériques, présentation de différents usages, notamment pour le rendu lumineux 3D

Bibliographie

• Isaac Todhunter, An elementary treatise on Laplace's functions, Lame's functions and Bessel's functions, Macmillan and Co, 1875.
• Norman McLeod Ferrers, An elementary treatise on spherical harmonics and subjects connected with them, Macmillan and Co, 1877.
• William Ellwood Byerly, An elementary treatise on Fourier's series and spherical, cylindrical, and ellipsoidal harmonics with applications to problems in mathematical physics, Ginn & Co, 1893.
• René Lagrange, Polynômes et fonctions de Legendre Modèle:Coll., Modèle:N°, Gauthier-Villars, 1939.
• I.S. Gradshteyn et I.M. Ryzhik, Table of Integrals, Series, and Products, éd. Alan Jeffrey and Daniel Zwillinger, Academic Press (Modèle:6e, 2000) Modèle:ISBN. Errata sur le site web des éditeurs : [http ://www.mathtable.com/gr/ www.mathtable.com].
• John D. Jackson, Électrodynamique classique — Cours et exercices d'électromagnétisme, Dunod, 2001) Modèle:ISBN. Traduction française de la Modèle:3e du grand classique américain.
• Modèle:Basdevant.
• Modèle:Cohen.
• Modèle:Messiah.
• H.-J. Bunge, Texture analysis in materials science — Mathematical methods, éd. Butterworths, 1969 (1982 pour la trad. en anglais) : pour les harmoniques sphériques généralisées.
• Yvette Kosmann-Schwarzbach, Groupes et symétries : groupes finis, groupes et algèbres de Lie, représentations, éditions de l'École polytechnique, Modèle:Date- ; chapitre 7, « Les harmoniques sphériques » Modèle:ISBN.