Masse volumique de l'air

La masse volumique de l'air $\rho$ (rho) caractérise la masse d'air qui est contenue dans un mètre cube. Elle se mesure en kilogrammes par mètre cube (kg/mModèle:3). À une altitude donnée, l'air subit une pression induite par la masse de la colonne atmosphérique située au-dessus. La masse volumique de l'air est plus importante au niveau de la mer (Modèle:Unité à Modèle:Tmp) et décroît avec l'altitude.

Variation de la masse volumique avec l'altitude et la température

Pression et masse volumique moyennes de l'air en fonction de l'altitude

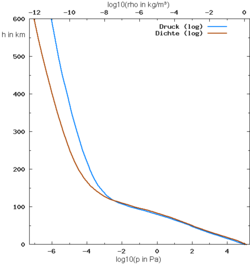
Au sol, l'air a une plus grande masse volumique, une plus grande pression et, sauf en cas d'inversion météorologique, une température plus élevée. Il devient moins dense quand l'altitude augmente. Si la température était constante quelle que soit l'altitude, la pression et la masse volumique de l'air diminueraient de la même manière avec l'altitude, d'après la formule de nivellement barométrique :

$p(h_1)=p(h_0)e^{-\frac{\mathrm{\Delta }h}{h_s}}$ avec $h_s=\frac{RT}{Mg}$.

La température varie toutefois de manière importante suivant l'altitude : voir les différentes formules de nivellement barométrique.

La diminution théorique de la pression et de la masse volumique de l'air, qui devraient diminuer de moitié tous les cinq mille mètres, n'est pas tout à fait exacte, mais constitue une bonne approximation.

• 90 % de l'atmosphère est située en dessous de Modèle:Unité d'altitude.
• 75 % de l'atmosphère est située en dessous de Modèle:Unité d'altitude.
• 50 % de l'atmosphère est située en dessous de Modèle:Unité d'altitude.

Masse volumique de l'air sec

D'après la loi des gaz parfaits, la masse volumique de l'air s'écrit :

$\rho =\frac{PM}{RT}$ Modèle:Spaces (kg/mModèle:3)

avec :

• P, la pression de l'air (Pa) ;
• M, la masse molaire de l'air (kg/mol) ;
• R, la constante universelle des gaz parfaits (8,3144621 J·K^-1·mol^-1) ;
• T, la température (K).

En choisissant pour pression celle de l'atmosphère standard internationale (ISA) au niveau de la mer : P₀ = Modèle:Unité = Modèle:Unité = Modèle:Unité :

• pour T₀ = Modèle:Unité (Modèle:Tmp) : ρ₀ = Modèle:Unité ;
• pour TModèle:Ind = Modèle:Unité (Modèle:Tmp), température de l'atmosphère ISA : ρ₁₅ = Modèle:Unité ;
• pour T₂₀ = Modèle:Unité (Modèle:Tmp) : ρ₂₀ = Modèle:Unité ;
• pour T₂₅ = Modèle:Unité (Modèle:Tmp) : ρ₂₅ = Modèle:Unité.

Ceci est généralisé en : $\rho =1,292\cdot \frac{273,15}{T}$ avec T en K.

Masse volumique de l'air humide

Une valeur plus précise de la masse volumique de l'air peut être obtenue en tenant compte de l'humidité de l'air, car cette dernière modifie la constante spécifique de l'air $R_{\text{h}}$. La masse volumique de l'air humide s'écrit : $\rho =\frac{p}{R_{\text{h}}T}$.

La constante spécifique de l'air humide s'écrit : $R_{\text{h}}=\frac{R_{\text{s}}}{1-(\phi \cdot p_{\text{sat}}/p)\cdot (1-R_{\text{s}}/R_{\text{v}})}$

avec :

• $R_{\text{s}}=$ Modèle:Unité est la constante spécifique de l'air sec ;
• $R_{\text{v}}$ = Modèle:Unité est la constante spécifique de la vapeur d'eau ;
• $\phi$ est l'humidité relative (0,76 correspond à 76 %) ;
• et $p$ est la pression de l'air.

$p_{\text{sat}}$ est la pression de vapeur saturante de l'eau dans l'air, et se détermine par exemple avec la formule de MagnusModèle:Refnec :

$p_{\text{sat}}=611,213\cdot \exp \left(\frac{17,5043\cdot \vartheta }{241,2{}^{\circ }\mathrm{C}+\vartheta }\right)$

où $\vartheta$ est la température en degrés Celsius. Cette formule est valable pour $\vartheta$ entre Modèle:Tmp et +Modèle:Tmp et donne la pression en pascals.

On peut également utiliser la formuleModèle:Refnec :

$p_{\text{sat}}=611,657\cdot \exp (17,2799-\left(\frac{4102,99}{(\vartheta +273,15)-35,719}\right))$

D'où, finalement :

$\rho (\phi ,\vartheta ,p)=\frac{1}{R_{\text{s}}\cdot (\vartheta +273,15)}(p-230,617\cdot \phi \cdot \exp \left[\frac{17,5043\cdot \vartheta }{241,2{}^{+}\vartheta }\right])$

avec :

• $\phi$, l'humidité relative ;
• $\vartheta$, la température en °C ;
• $p$, la pression en Pa.

Des données plus précises peuvent être trouvées dans les tables thermodynamiques.

Pour minimiser les erreurs de mesure, il est recommandé d'utiliser un psychromètre à aspiration pour déterminer l'humidité de l'air, et un baromètre à mercure pour déterminer la pression ambiante (la mesure donnée par le baromètre doit être corrigée des écarts dus à la capillarité, à la hauteur du ménisque convexe, à la densité du mercure (qui dépend de la température) et à l'accélération de la pesanteur locale).

Table

Masse volumique de l'air sec
en fonction de la température à p₀ = Modèle:Unité

$\vartheta$ en °C	ρ en kg/mModèle:3		$\vartheta$ en °C	ρ en kg/mModèle:3
−10	1,341		+40	1,127
−5	1,316		+45	1,110
0	1,292		+50	1,092
+5	1,269		+55	1,076
+10	1,247		+60	1,060
+15	1,225		+65	1,044
+20	1,204		+70	1,029
+25	1,184		+75	1,014
+30	1,164		+80	1,000
+35	1,146		+85	0,986

Articles connexes

• Air
• Hygrométrie

Liens externes

• Table : masse volumique de l'air humide en fonction de l'humidité relative et de la température, sur thermexcel.com.