Quantification (logique)

Symboles mathématiques des deux quantificateurs logiques les plus courants.

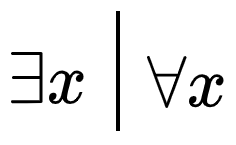
En mathématiques, les expressions « pour tout » (ou « quel que soit ») et « il existe », utilisées pour formuler des propositions mathématiques dans le calcul des prédicats, sont appelées des quantifications. Les symboles qui les représentent en langage formel sont appelés des quantificateurs (ou autrefois des quanteursModèle:,).

Quantification universelle

La quantification universelle (« pour tout ... » ou « quel que soit ... ») se dénote par le symbole $\mathrm{\forall }$ (un A à l'envers).

Exemple :

$\mathrm{\forall }xP(x)$

se lit

$\text{Pour tout}xP(x)$

et signifie

« tout objet du domaine considéré possède la propriété $P$ ».

La notation « $\mathrm{\forall }$ » a été utilisée pour la première foisModèle:, par Gerhard Gentzen en 1933 (publié en 1934). Le mot allemand Modèle:Lang signifiant « tout », il propose un Modèle:Citation. Gentzen indique qu'il a choisi comme « symbole pour tout » (Modèle:Lang) le A renversé par analogie avec le symbole « $\mathrm{\exists }$ » pour le quantificateur existentiel qu'il tient de Russell (qui lui-même l'a emprunté à Peano).

Quantification existentielle

La quantification existentielle (« il existe un ... » au sens « il existe au moins un ... ») se note avec le signe $\mathrm{\exists }$ (le symétrique axial d'un E, c'est-à-dire, la lettre Ə majuscule). Plus précisément,

$\mathrm{\exists }xP(x)$

signifie

$\text{il existe au moins un}x\text{tel que}P(x).$ (un objet au moins du domaine considéré possède la propriété $P$)

Pour exprimer l'unicité en plus de l'existence, le signe utilisé est $\mathrm{\exists }!$ (le quantificateur existentiel suivi d'un point d'exclamation), plus précisément,

$\mathrm{\exists }!xP(x)$

signifie

$\text{il existe un unique }x\text{ tel que }P(x)$, ou encore $\text{il existe un et un seul }x\text{ tel que }P(x)$ (un objet exactement du domaine considéré possède la propriété $P$).

Ce dernier quantificateur se définit en calcul des prédicats égalitaire à partir des deux quantificateurs précédents (et de l'égalité), par exemple par

$\mathrm{\exists }!xP(x)\equiv \mathrm{\exists }x[P(x)\text{et}\mathrm{\forall }y(P(y)⟹y=x)]$

La notation $\mathrm{\exists }$ a tout d'abord été employée par Giuseppe Peano en 1897 dans le volume II de son Formulaire de mathématiques avec une syntaxe différente, le signe étant directement associé au prédicat ($\mathrm{\exists }P$ pour notre $\mathrm{\exists }xP(x)$). Bertrand Russell l'utilise le premier de la façon actuelle, comme un opérateur de liaison.

Négation des quantificateurs

La négation de $\mathrm{\exists }xP(x)$ est

$\mathrm{\neg }\mathrm{\exists }xP(x)$, soit : $\mathrm{\forall }x\mathrm{\neg }P(x)$.

La négation de $\mathrm{\forall }xP(x)$ est

$\mathrm{\neg }\mathrm{\forall }xP(x)$, soit $\mathrm{\exists }x\mathrm{\neg }P(x)$ en logique classique, mais pas en logique intuitionniste.

Ordre des quantificateurs

Pour une formule mise en forme prénexe, l'ordre des quantificateurs entre chaque bloc de quantificateurs identiques (donc bloc de quantificateurs existentiels ou bloc de quantificateur universels) est indifférent, la formule restant la même. Par contre, l'alternance des blocs de quantificateurs existentiels ou universels donne des formules bien distinctes dont la complexité logique s'observe notamment dans la hiérarchie arithmétique.

Déduction naturelle

En déduction naturelle, Gerhard Gentzen présente les deux quantificateurs de la manière suivante:

	Règles d'introduction	Règles d'élimination
pour tout	$\frac{F}{\mathrm{\forall }xF}$.	$\frac{\mathrm{\forall }xF}{F}$
il existe	$\frac{F}{\mathrm{\exists }xF}$	$\frac{\mathrm{\exists }xF\begin{array}{c}[F]\\ ⋮\\ q\end{array}}{q}$

Exemples

Si l'on prend un groupe de chats noirs, on peut dire que quel que soit le chat que l'on choisit dans ce groupe, il sera noir. ($\mathrm{\forall }\text{chat dans ce groupe,}\text{ la couleur du chat est noire}$)

Si, dans un groupe de chats noirs, il y a quelques chats blancs (ou un seul), on peut dire qu'il existe un (ou un unique) chat de couleur blanche dans ce groupe.

($\mathrm{\exists }!\text{chat dans ce groupe, la couleur du chat est blanche}$)

Représentation des quantificateurs en Unicode, HTML et LaTeX

	Symbole	Unicode	HTML	LaTeX
pour tout	∀	U+2200	∀	\forall
il existe	∃	U+2203	∃	\exists

Bibliographie

L'exposé des règles régissant les quantificateurs usuels il existe et quel que soit se trouve dans tous les manuels de calcul des prédicats dont une bibliographie peut être trouvée sur logique mathématique.

Pour une généalisation de ces quantificateurs on peut se tourner vers :

• Modèle:En Generalized Quantifiers and Computation: 9th European Summer School in Logic, Language, and Information ESSLLI’97Workshop Aix-en-Provence, France, August 11–22, 1997 Revised Lectures, 145 pages, Modèle:Isbn

Voir aussi

• Théorie de la description définie de Bertrand Russell
• Théorie des mondes possibles
• Notation (mathématiques)
• La lettre λ du Lambda-calcul qui elle aussi lie des variables.