Registre à décalage à rétroaction linéaire

Un registre à décalage à rétroaction linéaire, ou LFSR (sigle de l'anglais Modèle:Lang), est un dispositif électronique ou logiciel qui produit une suite de bits qui peut être vue comme une suite récurrente linéaire sur le corps fini F₂ à 2 éléments (0 et 1). La notion a été généralisée à n'importe quel corps fini.

Réalisé électroniquement, dans le cas particulier d'une suite de 0 et de 1, c'est un registre à décalage avec rétroaction linéaire, ce qui signifie que le bit entrant est le résultat d'un OU exclusif (ou XOR) entre plusieurs bits du registre, cette opération étant également l'addition sur le corps fini F₂. Ces dispositifs sont simples, peu coûteux et efficaces.

La suite récurrente produite par un LFSR est nécessairement périodique à partir d'un certain rang. Les LFSR sont utilisés en cryptographie pour engendrer des suites de nombres pseudo-aléatoires. La fonction de rétroaction est alors choisie de façon à obtenir une période la plus grande possible.

L’étendue des applications est très large : chiffrement des communications, contrôle d'erreurs sur la transmission de données, auto-test des composants électroniques…

Fonctionnement

Principe

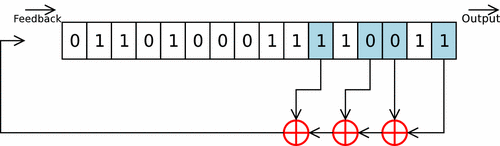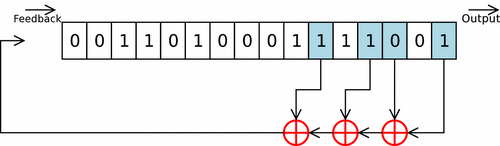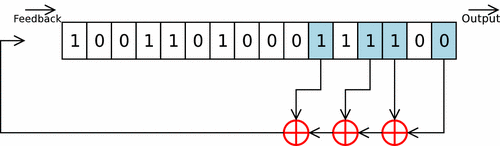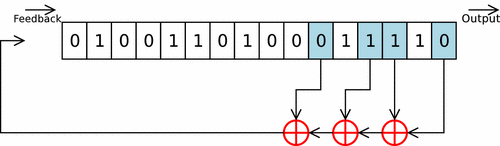
Un LFSR est un dispositif dérivé du registre à décalage de type SIPO, Serial In - Parallel Out, dans lequel un ou plusieurs « étages » du registre subissent une transformation pour être réinjectés en entrée de celui-ci^[1].

Il est dit de longueur « $r$ » lorsqu'il est composé de $r$ éléments appelés « étages » ou « cellules », le contenu de l'ensemble de ces éléments à un moment « $t$ » est l'état du LFSR à ce moment^[2]. À chaque top d'horloge le contenu d'un étage est transféré au suivant et le premier est rempli par le résultat d'une fonction linéaire qui prend en compte l'état d'un ou de plusieurs étages^[2]. Modèle:Clr

Exemple

LFSR à 4 bits^[3]
Horloge	État du LFSR	Sortie
0	`0 1 1 0`
1	`1 0 1 1`	`0`
2	`0 1 0 1`	`1`
3	`0 0 1 0`	`1`
4	`0 0 0 1`	`0`
5	`1 0 0 0`	`1`
6	`1 1 0 0`	`0`
7	`0 1 1 0`	`0`

Exemple des états successifs d'un LFSR à 4 bits avec une connexion des premier, second et quatrième étages au niveau de la fonction de retour^[3] :

à $t = 0$ l'état initial du LFSR est 0 1 1 0 ;
à $t = 1$ le bit d'entrée vaut 1 $(0 \oplus 1 \oplus 0)$ , l'état du LFSR est 1 0 1 1 et le bit de sortie vaut 0 ;
à $t = 2$ le bit d'entrée vaut 0 $(1 \oplus 0 \oplus 1)$ , l'état du LFSR est 0 1 0 1 et le bit de sortie vaut 1 ;
à $t = 3$ le bit d'entrée vaut 0 $(0 \oplus 1 \oplus 1)$ , l'état du LFSR est 0 0 1 0 et le bit de sortie vaut 1 ;
à $t = 4$ le bit d'entrée vaut 0 $(0 \oplus 0 \oplus 0)$ , l'état du LFSR est 0 0 0 1 et le bit de sortie vaut 0 ;
à $t = 5$ le bit d'entrée vaut 1 $(0 \oplus 0 \oplus 1)$ , l'état du LFSR est 1 0 0 0 et le bit de sortie vaut 1 ;
à $t = 6$ le bit d'entrée vaut 1 $(1 \oplus 0 \oplus 0)$ , l'état du LFSR est 1 1 0 0 et le bit de sortie vaut 0 ;
à $t = 7$ le bit d'entrée vaut 0 $(1 \oplus 1 \oplus 0)$ , l'état du LFSR est 0 1 1 0 et le bit de sortie vaut 0.

Au septième top d'horloge l'état du registre est identique à son état initial. On dit que le LFSR est de période 7. Modèle:Clr

Modèles mathématiques

Conception

Un LFSR est défini comme suit sur un corps fini $𝔽_{p^{n}}$ où $p$ est premier et $n \geq 1$ ^[4] :

un entier $r$ qui est sa taille ;
un état initial $S_{r - 1} = (a_{0}, a_{1}, \dots, a_{r - 1})$ à éléments sur $𝔽_{p^{n}}$ ;
une fonction linéaire de retour $f ()$ ;
on calcule $a_{r} = f (a_{0}, a_{1}, \dots, a_{r - 1})$ ;
on fait entrer $a_{r}$ et fait sortir $a_{0}$ ;
on obtient une nouvelle séquence de sortie $S_{r} = (a_{1}, a_{2}, \dots, a_{r})$ .

Définitions

Un LFSR peut être défini comme un triplet $L = (𝔽_{q}, r, (c_{1}, c_{2}, . . ., c_{r}))$ , où F_q est le corps fini à q éléments, r est le nombre de cellules du LFSR, les coefficients c₁, …, c_r sont des éléments de F_q^[5].

Suite engendrée: La suite engendrée par ce LFSR est une suite $(a_{n})_{n \in ℕ}$ vérifiant la relation de récurrence

$a_{n} = \sum_{i = 1}^{i = r} c_{i} a_{n - i}$ , pour $n \geq r$ ^[5]
ou de façon équivalente
$a_{r + n} = \sum_{j = 0}^{r - 1} c_{r - j} a_{n + j}$ ^[1].

Taille: La taille du LFSR est r le nombre de cellules.
Coefficients de connexion: les coefficients c₁, …, c_r sont appelés les coefficients de connexion du LFSR^[5].
Fonction de retour ou de rétroaction: La fonction f définie par
$f (x_{1}, x_{2}, . . ., x_{r - 1}, x_{r}) = c_{1} x_{1} + c_{2} x_{2} + . . . + c_{r - 1} x_{r - 1} + c_{r} x_{r}$
est appelée fonction de retour ou de rétroaction du LFSR^[2]. Quand q=2, F₂ est le corps des booléens et f est une fonction booléenne (linéaire).
Fonction génératrice: La fonction génératrice de la suite engendrée par un LFSR sur le corps F_q est la série formelle de F_q [[X]] définie par^[6]Modèle:,^[7]
$A (X) = \sum_{n = 0}^{\infty} a_{n} X^{n}$

Représentations polynomiales

Modèle:Section à recycler

Polynôme de rétroaction: Soit un LFSR $L$ défini par le triplet $(𝔽_{p^{n}}, r, (c_{1}, c_{2}, . . ., c_{r}))$ . Son polynôme de rétroaction, appelé aussi polynôme caractéristique, est $T (X) = 1 + \sum_{i = 1}^{r} c_{i} X^{i}$ ^[8].; Exemple : Un LFSR $L = (𝔽_{2}, 7, (1, 0, 1, 1, 0, 0, 1))$ aura comme polynôme de rétroaction $T (X) = 1 + X^{1} + X^{3} + X^{4} + X^{7}$ .

Polynôme de connexion: Pour un LFSR défini par le triplet $L = (𝔽_{p^{n}}, r, (c_{1}, c_{2}, . . ., c_{r}))$ , le polynôme de connexion est $q (X) = \sum_{i = 1}^{r} c_{i} X^{i} - 1$ dans $𝔽_{p^{n}} [[X]]$ ^[6]Modèle:,^[7].; Exemple : Un LFSR $L = (𝔽_{2}, 7, (1, 0, 1, 1, 0, 0, 1))$ aura comme polynôme de connexion $q (X) = X^{7} + X^{4} + X^{3} + X^{1} - 1$ .

Périodicité

Modèle:Section à recycler Puisque la prochaine valeur d'entrée d'un LFSR dépend uniquement des valeurs de certains étages de celui-ci et que l'état « tout à zéro » ne génère jamais de changement sa séquence est de période maximale $q^{r} - 1$ sur $𝔽_{q}$ où $r$ est la taille du registre^[9]Modèle:,^[10].

Une séquence d'un LFSR sur $𝔽_{q}$ avec une période $q^{r} - 1$ où $r$ est la taille du registre est appelé une « m-sequence »^[3]Modèle:,^[9].

Exemple : Un LFSR $L = (𝔽_{2}, 7, (1, 0, 1, 1, 0, 0, 1))$ aura une période maximale de $2^{7} - 1 = 127$ .

Algorithme de Berlekamp-Massey

Introduit en 1969 par James Massey l'algorithme de Modèle:Lien permet d'obtenir le plus petit LFSR possible pour une séquence de sortie choisie^[11]. Il suffit de capter $2 r$ bits consécutifs d'une m-séquence de période $2^{r} - 1$ pour pouvoir reconstruire la séquence entièrement^[12].

Description de l'algorithme^[13] :

En entrée : les $2 n$ éléments d'une séquence récurrente de manière linéaire définie sur $𝕂$ avec $n \in ℕ$ donnés par la liste $(a_{0}, a_{1}, \dots, a_{2 n - 1})$ . Le polynôme minimal est de degré limite $n$ .

En sortie : le polynôme $P (x)$ caractéristique minimal de la séquence.

Début

Variables locales

R, R_{0}, R_{1}, V, V_{0}, V_{1}, Q

sont des polynômes de

x

.

Initialisation

R_{0} : = x^{2 n}; R_{1} : = \sum_{i = 0}^{2 n - 1} a_{i} x^{i}; V_{0} = 0; V_{1} = 1;

Boucle, tant que

n ⩽ d e g (R 1)

faire :

Q : =

quotient de la division de

R_{0}

par

R_{1};

R : =

reste de la division de

R_{0}

par

R_{1};

V : = V_{0} - Q V_{1}

V_{0} : = V_{1}

V_{1} : = V

R_{0} : = R_{1}

R_{1} = R

Fin boucle

d : = m a x (d e g (V_{1}), 1 + d e g (R_{1})); P : = x^{d} V_{1} (1 / x);

Retour

P : = P / leadcoeff (P)

.

Fin

Modes de connexion

La représentation employée jusqu'ici pour représenter la connexion entre les différents étages du registre décrit le mode dit de « Fibonacci ». Une autre représentation est possible, utilise le mode dit de « Galois »^[14].

Fibonacci

Un registre en mode Fibonacci applique strictement la définition d'un LFSR : les contenus des différents étages sont ajoutés ou non les uns aux autres, le résultat de cette addition est ensuite placé dans l'étage d'entrée du registre et tous les étages subissent un décalage vers la sortie^[15]. Modèle:Clr

Galois

Dans le mode dit de Galois le contenu de l'étage de sortie est ajouté ou non au contenu des étages du registre puis tous les étages subissent un décalage vers la sortie et le contenu de l'étage sortant est réinjecté dans l'étage d'entrée^[16].

Au niveau matériel les LFSRs sont souvent mis en œuvre en utilisant ce mode car celui-ci est plus rapide et présente moins de latence que le mode Fibonacci puisque les étages sont mis à jour simultanément^[17]Modèle:,^[18]. Modèle:Clr

Applications

Les LFSRs existent sous deux formes: matérielle et logicielle, mais c'est surtout la première configuration qui est utilisée car elle est simple à mettre en œuvre (matériel peu onéreux associé à un algorithme de traitement simple)^[14].

L'usage de cette technologie peut se retrouver dans les domaines suivants^[3] :

Générateur de nombres pseudo-aléatoires ;
Algorithmes de chiffrement des données (Cryptographie, Stéganographie) ;
Détection d'erreurs et correction de données ;
Auto-contrôle des circuits électroniques ;
Traitement numérique du signal ;
Compteurs à base de LFSRs ;
Autres utilisations des LFSRs (Jeux vidéo, radar…).

Génération de nombres pseudo-aléatoires

Modèle:Article détaillé

Il y a eu beaucoup de publications à propos de la génération des nombres pseudo-aléatoires par les registres à décalage et à part quelques études sur les Modèle:Lien, la majorité des auteurs utilisent la rétroaction linéaire^[2].

Un problème fondamental en cryptologie est la production de suites de bits « aussi aléatoires que possible ». Un exemple évident étant la génération des clefs de chiffrement (symétrique ou asymétrique)^[19].

Ce problème se décompose en fait en deux parties :

La génération de bits par des procédés physiques, dans le cas d'un ordinateur des mesures liées à l'activité de la machine (températures interne, déplacement de la souris, etc.)
L'expansion d'une courte suite aléatoire de bits en une suite éventuellement beaucoup plus grande; Dans ce dernier cas, on parle de suite pseudo-aléatoire.

Chiffrement des données

Cryptographie

Modèle:Article détaillé

Les générateurs pseudo-aléatoires à base de LFSR sont utilisés dans les chiffrements de flux que l'on retrouve sous le terme anglais cipher stream^[20], ils constituent avec les chiffrements par bloc les 2 grandes catégories modernes du chiffrement symétrique de la cryptographie.

Les LFSRs sont les composants de base de nombreux générateurs chiffrants^[21].

Les raisons pour lesquelles les LFSRs sont utilisés dans un grand nombre de générateurs de flux sont les suivantes^[21] :

Les LFSRs sont bien adaptés à une configuration matérielle ;
Ils peuvent produire des grandes périodes de séquences binaires ;
Les séquences produites ont des bonnes propriétés statistiques ;
En raison de leur nature, ils peuvent être facilement analysés en utilisant des modèles mathématiques.

Cependant, l'utilisation des LFSRs dans leur configurations initiales est devenue très vite vulnérable aux attaques mathématiques (démontré par l'algorithme de Berlekamp-Massey).

Un système informatique pour ne pas être vulnérable doit être sécurisé contre les attaques connues et référencées, c'est pourquoi un LFSR ne doit jamais être utilisé par lui-même comme un générateur de flux de clés^[22].

Néanmoins, les LFSRs restent encore utilisés en raison de leurs coûts de mise en œuvre très bas^[22].

Trois méthodes peuvent être employées pour contourner l'effet des propriétés de linéarité des LFSRs^[22] :

Associer une fonction non linéaire aux sorties de plusieurs LFSRs ;
Utiliser une fonction de filtrage non linéaire basé sur le contenu d'un seul LFSR ;
Utiliser plusieurs LFSRs en parallèle ou une horloge externe qui peut provenir d'un autre LFSR^[23].

Les propriétés attendues d'un générateur de flux de chiffrement sont^[22] :

Une grande période ;
Grande complexité linéaire ;
Bonnes propriétés statistiques.

Exemples d'algorithmes cryptographiques utilisant les LFSRs :

Codage/décodage des transmissions des téléphones cellulaires
A5/1 : chiffrement des communications GSM^{[note 1]}, il utilise 3 LFSRs de 19, 22 et 23 bits (64 bits au total) ;
Codage du Bluetooth
E0 : protocole de codage du Bluetooth utilisant quatre LFSR de longueurs 25, 31, 33, et 39 bits (128 bits au total)^[24].

Stéganographie

Modèle:Article détaillé

La stéganographie est la technique qui permet de cacher de l'information, le plus souvent un texte dans des images, une des méthodes est de remplacer le bit de poids faible de chaque pixel formant l'image par un autre bit d'information^[25].

Les séquences pseudo-aléatoires à base de LFSRs sont une des méthodes de chiffrement de l'information^[25].

Embarqués dans des circuits logiques programmables tels que les FPGA^{[note 2]}, ils répondent à un besoin croissant de cacher l'information^[26]. Modèle:Clr

Détection d'erreurs et correction de données

Plusieurs types de CRC selon les applications^[3]
Application	Type	taille LFSR
CRC	CRC-12	12
	CRC-16	16
Réseau ATM^{[note 3]}	CRC-32	32

Ce mécanisme que l'on appelle contrôle de redondance cyclique et que l'on retrouve sous le nom de CRC^{[note 4]} est un dispositif de contrôle d'erreur lors des transmissions de données brutes dans le domaine du réseau, le stockage numérique ou encore dans la compression de donnée^[27].

Les composants hardware LFSR sont un des moyens faciles et bon marché pour générer des suites pseudo-aléatoires utilisées par ces procédés^[27].

Modèle:Clr

Auto-contrôle des circuits électroniques

Le test des circuits électroniques a été longtemps problématique car les solutions existantes donnant des temps de réponses corrects étaient souvent très onéreuses. Le coût n'est pas le seul problème, il faut aussi que le dispositif puisse répondre à 2 problématiques^[28] :

Le temps : Il ne faut pas que le mécanisme consomme trop de temps à générer l'échantillonnage de test au détriment de l'efficacité du composant ;
Le volume de donnée : La taille de échantillonnage peut devenir tellement grande que le test n'est plus efficace.

La technologie BIST^{[note 5]} est une méthode de test des composants électroniques qui s'appuie sur plusieurs mécanismes^[29] :

Technique de parité ;
Technique de comptage ;
LFSRs.

Les tests aléatoires sur une partie du composant suppose de pouvoir agir sur un échantillonnage des données du composant^[30].

Traitement numérique du signal

C'est l’étude du traitement du signal numérisé tel que le filtrage ou la compression, elle est assurée par un processeur de signal numérique que l'on retrouve indiqué dans ce domaine par DSP^{[note 6]}. Ces opérations seraient difficilement réalisables directement sur les données binaires en mémoire sans algorithme de compression/décompression.

Les LFSRs sont fréquemment utilisés pour cette tache car ils sont efficaces dans le traitement de grande quantité de données binaires et ils ont un faible cout d’implémentation dans leurs formes matériels ^[31].

Compteurs à base de LFSRs

Les compteurs binaires sont des composants qui sont utilisés couramment dans des équipements nécessitant un comptage comme, par exemple, les montres digitales ou les chronomètres.

Un LFSR est un type spécial de compteur qui génère une séquence pseudo-aléatoire, il peut être utilisé en remplacement des compteurs binaires traditionnels^[32].

Exemples d'utilisation^[33]:

Compteurs à incrément ou décrément 'up/down counters' ;
- Down counters - commence à w/ 111 ;
- Utilise une porte 'XOR' pour la retroaction ;
- L'initialisation ne doit pas être que des zéros.
'Up counters' commence à w/ 000.

Utilisation du XNOR

Avantages^[34]	Inconvénients^[34]
Nécessite peu de logique pour être mis en place ; Les compteurs avec des grandes valeurs restent efficaces ; Pas de besoin d'un nombre élevé de portes logiques ; Ils sont très rapides. Les erreurs sont détectables typiquement un timer 2*n.	Besoin d'initialiser le registre pour avoir un état valide ; Certaines applications ont besoin d'une séquence binaire ; Pas de moyen simple de prédire la séquence de comptage.

Modèle:Clr

Autres utilisations des LFSRs

L'industrie du jeu vidéo a utilisé le LFSR au travers d'un composant qui est le SN76489, on a pu ainsi sonoriser certaines consoles de jeux vidéo grâce à ce circuit électronique^[35].

Notes et références

Notes

Modèle:Références

Références

Modèle:Références

Bibliographie

Manuels et cours

Modèle:Ouvrage Modèle:Plume
Modèle:Ouvrage
Modèle:Ouvrage
Modèle:Ouvrage, en particulier le chapitre 4, « Cyclic Codes, Rings, and Polynomials » Modèle:Plume
Modèle:Ouvrage
Modèle:Ouvrage

Articles de recherche

Modèle:Légende plume

Liens externes

Registres à rétroaction linéaire sur www.apprendre-en-ligne.net
Modèle:En Simple VHDL coding for Galois and Fibonacci LFSR.
Les registres à décalages à rétroactions linéaires LFSR sur www.picsi.org
Les Générateurs Linéaires Congruentiels sur http://rng.free.fr

Modèle:Palette Modèle:Portail

↑ ^1,0 et ^1,1 Modèle:Harvsp
↑ ^2,0 ^2,1 ^2,2 et ^2,3 Modèle:Harvsp
↑ ^3,0 ^3,1 ^3,2 ^3,3 et ^3,4 Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^5,0 ^5,1 et ^5,2 Modèle:Harvsp
↑ ^6,0 et ^6,1 Modèle:Harvsp
↑ ^7,0 et ^7,1 Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^9,0 et ^9,1 Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^14,0 et ^14,1 Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^21,0 et ^21,1 Modèle:Harvsp
↑ ^22,0 ^22,1 ^22,2 et ^22,3 Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp.
↑ ^25,0 et ^25,1 Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^27,0 et ^27,1 Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ Modèle:Harvsp
↑ ^34,0 et ^34,1 Modèle:Harvsp
↑ Modèle:Harvsp

Erreur de référence : Des balises <ref> existent pour un groupe nommé « note », mais aucune balise <references group="note"/> correspondante n’a été trouvée

[A23p17-1] 1,0 et ^1,1 Modèle:Harvsp

[A3p191-2] 2,0 ^2,1 ^2,2 et ^2,3 Modèle:Harvsp

[A21p2-3] 3,0 ^3,1 ^3,2 ^3,3 et ^3,4 Modèle:Harvsp

[A34p8081-4] Modèle:Harvsp

[A34p81-5] 5,0 ^5,1 et ^5,2 Modèle:Harvsp

[A23p19-6] 6,0 et ^6,1 Modèle:Harvsp

[A34p83-7] 7,0 et ^7,1 Modèle:Harvsp

[A21p3-8] Modèle:Harvsp

[A23p18-9] 9,0 et ^9,1 Modèle:Harvsp

[A29p154-10] Modèle:Harvsp

[A35p505-11] Modèle:Harvsp

[A34p14-12] Modèle:Harvsp

[A31p76-13] Modèle:Harvsp

[A4p2-14] 14,0 et ^14,1 Modèle:Harvsp

[A22p2827-15] Modèle:Harvsp

[A22p2828-16] Modèle:Harvsp

[A33p437-17] Modèle:Harvsp

[A34p152-18] Modèle:Harvsp

[A55p11-19] Modèle:Harvsp

[A54p191-20] Modèle:Harvsp

[A54p195-21] 21,0 et ^21,1 Modèle:Harvsp

[A54p204-22] 22,0 ^22,1 ^22,2 et ^22,3 Modèle:Harvsp

[A48p17-23] Modèle:Harvsp

[25] Modèle:Harvsp.

[A40p239-26] 25,0 et ^25,1 Modèle:Harvsp

[A56p24-28] Modèle:Harvsp

[A12p11-31] 27,0 et ^27,1 Modèle:Harvsp

[A47p21-32] Modèle:Harvsp

[A47p25-34] Modèle:Harvsp

[A49p933-35] Modèle:Harvsp

[A4p1-37] Modèle:Harvsp

[A38p1-38] Modèle:Harvsp

[A52p3-39] Modèle:Harvsp

[A52p8-40] 34,0 et ^34,1 Modèle:Harvsp

[A53p1-41] Modèle:Harvsp

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[note 1]

[24]

[25]

[note 2]

[26]

[note 3]

[note 4]

[27]

[28]

[note 5]

[29]

[30]

[note 6]

[31]

[32]

[33]

[34]

[35]

Registre à décalage à rétroaction linéaire

Sommaire

Fonctionnement

Principe

Exemple

Modèles mathématiques

Conception

Définitions

Représentations polynomiales

Périodicité

Algorithme de Berlekamp-Massey

Modes de connexion

Fibonacci

Galois

Applications

Génération de nombres pseudo-aléatoires

Chiffrement des données

Cryptographie

Stéganographie

Détection d'erreurs et correction de données

Auto-contrôle des circuits électroniques

Traitement numérique du signal

Compteurs à base de LFSRs

Autres utilisations des LFSRs

Notes et références

Notes

Références

Bibliographie

Manuels et cours

Articles de recherche

Liens externes

Menu de navigation

Registre à décalage à rétroaction linéaire

Fonctionnement

Principe

Exemple

Modèles mathématiques

Conception

Définitions

Représentations polynomiales

Périodicité

Algorithme de Berlekamp-Massey

Modes de connexion

Fibonacci

Galois

Applications

Génération de nombres pseudo-aléatoires

Chiffrement des données

Cryptographie

Stéganographie

Détection d'erreurs et correction de données

Auto-contrôle des circuits électroniques

Traitement numérique du signal

Compteurs à base de LFSRs

Autres utilisations des LFSRs

Notes et références

Notes

Références

Bibliographie

Manuels et cours

Articles de recherche

Liens externes

Menu de navigation

Rechercher