Sectrice de Maclaurin

Sectrice de Maclaurin : exemple avec Modèle:Formule et Modèle:Formule

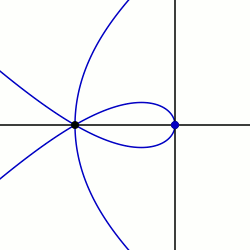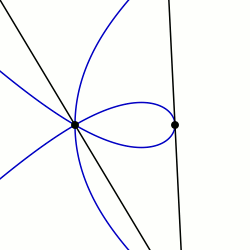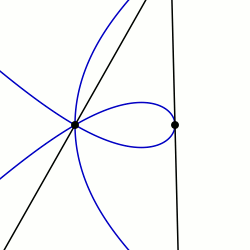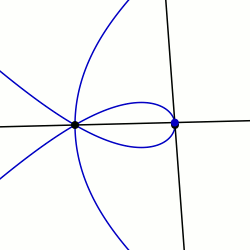
En géométrie, une sectrice de Maclaurin est définie comme la courbe parcourue par le point d'intersection de deux lignes qui tournent chacune à vitesse constante autour de points différents appelés pôles . De manière équivalente, une sectrice de Maclaurin peut être définie comme une courbe dont l'équation en coordonnées biangulaires est linéaire. Le nom est dérivé de la trisectrice de Maclaurin (du nom de Colin Maclaurin ), qui est un membre éminent de la famille, et de leur propriété sectrice, ce qui signifie qu'elles peuvent être utilisées pour diviser un angle en un nombre donné de parties égales. Il existe des cas particuliers connus sous le nom d'arachnides ou d'araneidées en raison de leur forme d' araignée, et des courbes de Plateau d'après Joseph Plateau qui les a étudiées.

Équations en coordonnées polaires

On considère deux droites en rotation autour de deux poles $P$ et $P_1$. Par translation et rotation on suppose que $P=(0,0)$ et $P_1=(a,0)$. Pour un paramètre $t$ réel, la droite en rotation autour de $P$ forme un angle $\theta =\kappa t+\alpha$ et celle en rotation autour de $P_1$ has angle ${\theta }_1={\kappa }_{1}t+{\alpha }_1$, avec $\kappa$, $\alpha$, ${\kappa }_1$ et ${\alpha }_1$ constantes. En éliminant $t$ pour obtenir l'égalité ${\theta }_1=q\theta +{\theta }_0$ avec $q={\kappa }_1/\kappa$ et ${\theta }_0={\alpha }_1-q\alpha$. On supposera $q$ rationnel, sinon la courbe n'est pas algébrique et devient dense dans le plan. Soit $Q$ le point d'intersection des deux droites et $\psi$ l'angle en $Q$, soit $\psi ={\theta }_1-\theta$. Si $r$ est la distance entre $P$ et $Q$ alors, par la loi des sinus,

$\frac{r}{\sin {\theta }_1}=\frac{a}{\sin \psi }$

donc

$r=a\frac{\sin {\theta }_1}{\sin \psi }=a\frac{\sin [q\theta +{\theta }_0]}{\sin [(q-1)\theta +{\theta }_0]}$

est l'équation en coordonnées polaires de la courbe parcourue par le point $Q$.

Le cas ${\theta }_0=0$ et $q=n$ où $n$ est un entier supérieur à 2 donne des courbes arachnides

$r=a\frac{\sin n\theta }{\sin (n-1)\theta }$

Le cas ${\theta }_0=0$ et $q=-n$ où $n$ est un entier supérieur à 1 donne des formes alternatives de courbes arachnides

$r=a\frac{\sin n\theta }{\sin (n+1)\theta }$

Une dérivation similaire à celle ci-dessus donne

$r_1=(-a)\frac{\sin [(1/q){\theta }_1-{\theta }_0/q]}{\sin [(1/q-1){\theta }_1-{\theta }_0/q]}$

comme l'équation polaire (en $r_1$ et ${\theta }_1$ ) si l'origine est décalée vers la droite de $a$. On notera qu'il s'agit de l'équation précédente avec un changement de paramètres ; cela est prévisible du fait que les deux pôles sont interchangeables dans la construction de la courbe.

Équations dans le plan complexe, coordonnées cartésiennes et trajectoires orthogonales

Soit $q=m/n$ où $m$ et $n$ sont des entiers et la fraction est exprimée dans ses termes les plus simples. Dans la notation de la section précédente, on a ${\theta }_1=q\theta +{\theta }_0$ ou $n{\theta }_1=m\theta +n{\theta }_0$ . Si $z=x+\mathrm{i}y$ alors $\theta =\arg (z),{\theta }_1=\arg (z-a)$, donc l'équation devient $n\arg (z-a)=m\arg (z)+n{\theta }_0$ ou $m\arg (z)-n\arg (z-a)=\arg (z^m(z-a{)}^{-n})=const$ . Cela peut aussi être écrit

$\frac{\mathrm{Re}(z^m(z-a{)}^{-n})}{\mathrm{Im}(z^m(z-a{)}^{-n})}=const.$

à partir de laquelle il est relativement simple de dériver l'équation cartésienne étant donné m et n. La fonction $w=z^m(z-a{)}^{-n}$ est analytique donc les trajectoires orthogonales de la famille $\arg (w)=const.$ sont les courbes $|w|=const$, ou $\frac{|z{|}^m}{|z-a{|}^n}=const.$

Équations paramétriques

Soit $q=m/n$ où $m$ et $n$ sont des entiers, et soit $\theta =np$ où $p$ est un paramètre. Alors , la conversion de l’équation polaire ci-dessus en équations paramétriques produit

$x=a\frac{\sin [mp+{\theta }_0]\cos np}{\sin [(m-n)p+{\theta }_0]},y=a\frac{\sin [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}$ .

L'application de la règle d'addition d'angle pour le sinus produit

$x=a\frac{\sin [mp+{\theta }_0]\cos np}{\sin [(m-n)p+{\theta }_0]}=a+a\frac{\cos [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}=\frac{a}{2}+\frac{a}{2}\frac{\sin [(m+n)p+{\theta }_0]}{\sin [(m-n)p+{\theta }_0]}$ .

Donc si l'origine est décalée vers la droite de a/2, alors les équations paramétriques sont

$x=\frac{a}{2}\cdot \frac{\sin [(m+n)p+{\theta }_0]}{\sin [(m-n)p+{\theta }_0]},y=a\frac{\sin [mp+{\theta }_0]\sin np}{\sin [(m-n)p+{\theta }_0]}$ .

Ce sont les équations des courbes de plateau lorsque ${\theta }_0=0$, ou

$x=\frac{a}{2}\frac{\sin (m+n)p}{\sin (m-n)p},y=a\frac{\sin mp\sin np}{\sin (m-n)p}$ .

Triplets inversifs

L'inverse par rapport au cercle de rayon $a$ et de centre à l'origine de

$r=a\frac{\sin [q\theta +{\theta }_0]}{\sin [(q-1)\theta +{\theta }_0]}$

est

$r=a\frac{\sin [(q-1)\theta +{\theta }_0]}{\sin [q\theta +{\theta }_0]}=a\frac{\sin [(1-q)\theta -{\theta }_0]}{\sin [((1-q)-1)\theta -{\theta }_0]}$ .

C'est une autre courbe dans la famille. L'inverse par rapport à l'autre pôle produit encore une autre courbe dans la même famille et les deux inverses sont à leur tour inverses l'un de l'autre. Par conséquent, chaque courbe de la famille est membre d’un triplet, dont chacune appartient à la famille et est l’inverse des deux autres. Les valeurs de $q$ dans cette famille sont

$q,\frac{1}{q},1-q,\frac{1}{1-q},\frac{q-1}{q},\frac{q}{q-1}$ .

Propriétés sectrices

Soit $q=m/n$ où $m$ et $n$ telle que q est irréductible et on suppose que ${\theta }_0$ est constructible à la règle et au compas . (La valeur de ${\theta }_0$ est généralement 0 dans la pratique, donc ce n'est normalement pas un problème.) Soit $\phi$ un angle donné et on suppose que la sectrice de Maclaurin a été dessinée avec des pôles $P$ et $P_1$ selon la construction ci-dessus. On construit un rayon à partir de $P_1$ d'angle $\phi +{\theta }_0$ et on note $Q$ le point d'intersection du rayon et de la sectrice et on trace $PQ$ . Si $\theta$ est l'angle de cette ligne alors

$\phi +{\theta }_0={\theta }_1=q\theta +{\theta }_0$

donc $\theta =\frac{n\phi }{m}$ . En soustrayant à plusieurs reprises $\theta$ et $\phi$ les uns des autres comme dans l' algorithme d'Euclide, l'angle $\phi /m$ peut être construit. Ainsi, la courbe est une m -sectrice, ce qui signifie qu'à l'aide de la courbe, un angle arbitraire peut être divisé par n'importe quel entier. Il s’agit d’une généralisation du concept de trisectrice et des exemples en seront trouvés ci-dessous.

On trace maintenant un rayon avec un angle $\phi$ depuis $P$ et soit $Q^{\prime }$ le point d'intersection de ce rayon avec la courbe. L'angle de $P^{\prime }{Q}^{\prime }$ est

${\theta }_1=q\theta +{\theta }_0=q\phi +{\theta }_0$

et en soustrayant ${\theta }_0$ on trouve un angle de

$q\phi =\frac{m\phi }{n}$ .

En appliquant à nouveau l'algorithme d'Euclide, on obtient un angle de $\phi /n$ montrant que la courbe est également une n -sectrice.

Enfin, on trace un rayon depuis $P$ avec angle $\pi /2-\phi -{\theta }_0$ et un rayon depuis $P^{\prime }$ avec angle $\pi /2+\phi +{\theta }_0$, et on note $C$ le point d'intersection. Ce point est situé sur la médiatrice de $P{P}^{\prime }$ , il y a donc un cercle avec un centre $C$ contenant $P$ et $P^{\prime }$ . $\mathrm{\angle }PC{P}^{\prime }=2(\phi +{\theta }_0)$ donc tout point du cercle forme un angle de $\phi +{\theta }_0$ entre $P$ et $P^{\prime }$ . (Il s'agit en fait d'un des cercles d'Apollinius de P et P' .) Soit $Q^{″}$ le point d'intersection de ce cercle et de la courbe. Alors $\phi +{\theta }_0=\mathrm{\angle }P{Q}^{″}{P}^{\prime }=\psi ={\theta }_1-\theta =(q-1)\theta +{\theta }_0$ donc

$\phi =\frac{(m-n)\theta }{n},\theta =\frac{n\phi }{m-n}$ .

L'application de l'algorithme d'Euclide une troisième fois donne un angle de $\phi /(m-n)$, montrant que la courbe est également une ( m − n )-sectrice.

Cas particuliers

q = 0

C'est la courbe

$r=a\frac{\sin {\theta }_0}{\sin (-\theta +{\theta }_0)}$

qui est une droite passant par $(a,0)$ .

q = 1

Il s'agit d'un cercle contenant l'origine et $(a,0)$ . Il a une équation polaire

$r=a\frac{\sin (\theta +{\theta }_0)}{\sin {\theta }_0}$ .

C'est la courbe inverse par rapport à l'origine du cas q = 0. Les trajectoires orthogonales de la famille des cercles sont la famille $\frac{|z-a|}{|z|}=const.$ Celles-ci forment les cercles d'Apollinius avec des pôles $(0,0)$ et $(a,0)$ .

q = -1

Ces courbes ont une équation polaire

$r=a\frac{\sin (-\theta +{\theta }_0)}{\sin (-2\theta +{\theta }_0)}$ ,

d'équation complexe $\arg (z(z-a))=const.$ En coordonnées cartésiennes, cela devient $x^2-y^2-x=c(2xy-y)$ qui est une conique. À partir de l'équation polaire, il est évident que les courbes ont des asymptotes pour $\theta ={\theta }_0/2$ et ${\theta }_0/2+\pi /2$ qui sont orthogonales. Les coniques sont donc en fait des hyperboles équilatères. Le centre de l'hyperbole est toujours $(a/2,0)$. Les trajectoires orthogonales de cette famille sont données par $|z||z-a|=c$ qui est la famille des ovales de Cassini avec des foyers en $(0,0)$ et $(a,0)$.

Trisectrice de Maclaurin

Dans le cas où $q=3$ (ou $q=1/3$ en inversant les pôles) et ${\theta }_0=0$, l'équation est

$r=a\frac{\sin 3\theta }{\sin 2\theta }=\frac{a}{2}\frac{4{\cos }^2\theta -1}{\cos \theta }=\frac{a}{2}(4\cos \theta -\sec \theta )$ .

Il s'agit de la trisectrice de Maclaurin qui est un cas particulier de la généralisation qu'est la sectrice de Maclaurin. La construction ci-dessus donne une méthode par laquelle cette courbe peut être utilisée comme une trisectrice.

Limaçon trisectrice et rosace

Dans le cas où $q=3/2$ (ou $q=2/3$ en inversant les pôles) et ${\theta }_0=0$, l'équation est

$r=a\frac{\sin \frac{3}{2}\theta }{\sin \frac{1}{2}\theta }=a(3{\cos }^2\frac{1}{2}\theta -{\sin }^2\frac{1}{2}\theta )=a(1+2\cos \theta )$ .

Il s'agit de la trisectrice de limaçon .

L'équation avec l'origine prise en l'autre pôle est une rosace qui a la même forme

$r=-a\frac{\sin \frac{2}{3}\theta }{\sin -\frac{1}{3}\theta }=2a\cos \frac{1}{3}\theta$ .

Le 3 dans le numérateur de q et la construction ci-dessus donnent une méthode permettant d'utiliser la courbe comme une trisectrice.

Références

• "Sectrice de Maclaurin" sur l'Encyclopédie des Formes Mathématiques Remarquables
• Modèle:MathWorld
• Modèle:MathWorld