Somme amalgamée

Diagramme commutatif traduisant la propriété universelle de la somme amalgamée.

En mathématiques, la somme amalgamée est une opération entre deux ensembles constituant les espaces d'arrivée de deux applications définies sur un même troisième ensemble. Le résultat satisfait une propriété universelle de factorisation de diagrammes, duale de celle du produit fibré et qui peut être valable dans d'autres catégories que celle des ensembles, comme celle des groupes. Dans la catégorie des espaces topologiques, la somme amalgamée intervient ainsi dans la description de certains espaces, dont le groupe fondamental se calcule alors à l'aide du théorème de van Kampen.

Par analogie avec la traduction anglaise de « produit fibré » (Modèle:Langue), la somme amalgamée est parfois désignée par sa traduction en Modèle:Langue (« poussé en avant »).

Définition ensembliste

Étant données deux applications définies sur un même ensemble :

$\begin{array}{c}Z\stackrel{g}{⟶}Y\\ f\downarrow \\ X\end{array}$

la somme amalgamée de Modèle:Math et Modèle:Math le long de Modèle:Math est définie comme le quotient de l'union disjointe de Modèle:Math et Modèle:Math par la relation d'équivalence engendrée par :

$f(z)\sim g(z)$

pour tout Modèle:Math dans Modèle:Math. Elle se note :

$X\bigsqcup _{Z}Y.$

La somme amalgamée étant un quotient de l'union disjointe, les injections canoniques induisent des applications qui permettent de compléter le carré commutatif :

$\begin{array}{ccc}Z& ⟶& Y\\ \downarrow & & \downarrow i_Y\\ X& \stackrel{i_X}{\to }& X\bigsqcup _{Z}Y\end{array}$

Dans des catégories ensemblistes, telles celles des espaces topologiques ou des espaces vectoriels, la somme amalgamée constitue elle-même un objet de la catégorie.

Propriété universelle

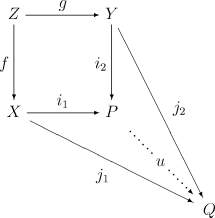
Avec les notations de la partie précédentes, si Modèle:Math est l'ensemble d'arrivée de deux applications définies respectivement sur Modèle:Math et Modèle:Math et permettant de construire un carré commutatif :

$\begin{array}{ccc}Z& ⟶& Y\\ \downarrow & & \downarrow j_Y\\ X& \stackrel{j_X}{⟶}& Q\end{array}$

alors il existe une unique application Modèle:Math de la somme amalgamée vers l'ensemble Modèle:Math qui factorise le diagramme :

$j_X=u\circ i_X{j}_Y=u\circ i_Y.$

Autrement dit, la somme amalgamée est la colimite du diagramme formé à l'aide des deux applications initiales Modèle:Math et Modèle:Math. Il est aussi possible de la voir comme la somme (au sens des catégories) dans une catégorie des morphismes partant de Modèle:Math.

Plus généralement, la somme amalgamée dans une catégorie quelconque est la colimite d'un tel diagramme, lorsqu'elle existe, ce qui est le cas dans les catégories abéliennes.

Voir aussi

Articles connexes

• Produit libre amalgamé
• Recollement (topologie)

Bibliographie

• Modèle:Godbillon1
• André Gramain, Topologie des surfaces, PUF, 1971