Théorème de vitesse moyenne

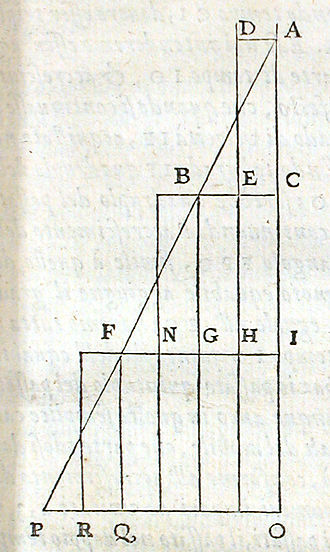
Au Modèle:S, les Calculateurs d'Oxford du Merton College ont découvert, et le savant français Nicole Oresme a démontré, le théorème dit règle de Merton sur l'accélération uniforme, ou encore théorème de Merton sur la vitesse moyenne[1].
En résumé, ce théorème dit qu'un corps uniformément accéléré à partir du repos, c'est-à-dire, d'une vitesse initiale égale à zéro, parcourt la même distance qu'un corps se déplaçant à une vitesse uniforme dont la vitesse est la moitié de la vitesse finale du corps[2].
Oresme généralise ce résultat et démontre géométriquement, en calculant l'aire d'un trapèze, que l'on a (avec les notations d'aujourd'hui) :
(la distance d parcourue est égale à la moitié de la somme de la vitesse initiale v0 et de la vitesse finale vf du mobile, multipliée par la durée t du mouvement) [3].
Les scientifiques médiévaux ont donc démontré ce théorème — fondement de la « loi de la chute des corps » — bien avant Galilée, qui en est généralement crédité.
Le physicien, mathématicien et historien des sciences Clifford Truesdell, a écrit à ce sujet[4] :
Des tablettes d'argile datées de –350 à –50 mésopotamiennes comportent d'ailleurs déjà des procédures utilisant des trapèzes pour calculer la position de Jupiter et prévoir son mouvement, et préfigurent ainsi le théorème du Modèle:S-[5].
Pour nous, le théorème découle simplement des équations cinématiques décrivant une accélération uniforme.
Voir aussi
Articles connexes
Lien externe
Notes
Bibliographie
- ↑ Edward Grant, A Source Book in Medieval Science (1974) Vol. 1, p. 252.
- ↑ Modèle:Ouvrage
- ↑ Modèle:Ouvrage.
- ↑ Modèle:Ouvrage.
- ↑ Modèle:Article