Cross-cap

Une cross-cap est le résultat d'une somme connexe entre une variété de dimension 2 et un plan projectif. Intuitivement, elle consiste à percer un trou dans une variété et à recoudre le bord en identifiant les points diamétralement opposés.

Exemples et propriétés

Deux vues de la sphère avec une cross-cap, formant le plan projectif. Deux autres immersions du plan projectif dans l'espace de dimension 3 sont données par la surface de Boy et la surface romaine.

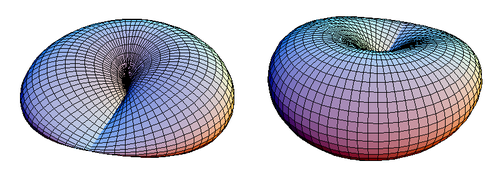
• une sphère avec une cross-cap est le plan projectif réel lui-même, la sphère étant élément neutre pour la somme connexe ;
• une sphère avec deux cross-caps a pour modèle la bouteille de Klein ;
• une sphère avec trois cross-caps est appelée surface de Dyck, et est homéomorphe à la somme connexe du plan projectif et du tore d'après un théorème de Walther von Dyck.

Dans une immersion dans RModèle:3, la cross-cap se traduit par une auto-intersection, à proximité de laquelle la cross-cap ressemble au parapluie de Whitney, donc possède des points cuspidaux.

Classification des variétés de dimension 2

Ces surfaces apparaissent dans le théorème de classification des variétés de dimension 2 : toute variété compacte de dimension 2 et sans bord est homéomorphe à la sphère (munie d'un certain nombre d'anses) avec 0, 1, ou 2 cross-caps. En effet, notons $T_1$ le tore, $T_n$ le tore à n trous (somme connexe de n tores $T_1$), $U_1$ le plan projectif, $U_n$ la somme connexe de n plans projectifs (ou la sphère munie de n cross-caps). $K=U_2$ est la bouteille de Klein, et le théorème de Dick énonce que $U_3=T_1\mathrm{\#}{U}_1$, et plus généralement, pour tout entier n, $U_{2n}=T_{n-1}\mathrm{\#}K$ et $U_{2n+1}=T_n\mathrm{\#}{U}_1$. On montre alors que toute surface compacte sans bord est homéomorphe à un $T_n$ (0 cross-cap) si elle est orientable, et à un $U_n$ si elle est non-orientable (tore à plusieurs trous muni de 1 cross-cap si n est impair, et 2 cross-caps si n est pair).

Liens externes

• Modèle:Lien web : animation d'une création d'une cross-cap.