Loi des cotangentes

Fig. 1. Notations usuelles dans un triangle.

Fig. 2. Six triangles rectangles.

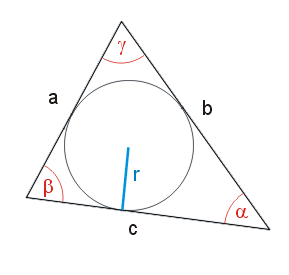
Modèle:Ébauche En géométrie du triangle, la loi des cotangentes est une relation entre les longueurs Modèle:Math, Modèle:Math et Modèle:Math des côtés d'un triangle et les cotangentes de ses angles moitiés Modèle:Sfrac, Modèle:Sfrac et Modèle:Sfrac :

$\frac{\cot (\frac{\alpha }{2})}{p-a}=\frac{\cot (\frac{\beta }{2})}{p-b}=\frac{\cot (\frac{\gamma }{2})}{p-c}=\frac{1}{r},$

où Modèle:Math désigne le demi-périmètre et Modèle:Math le rayon du cercle inscrit.

Démonstration

Découpons le triangle (cf. Fig. 2) en six triangles rectangles, symétriques deux par deux par rapport aux bissectrices et de côtés Modèle:Math, Modèle:Math et Modèle:Math, avec Modèle:Math, Modèle:Math et Modèle:Math. Alors, Modèle:Math donc Modèle:Math donc Modèle:Math donc Modèle:Sfrac = Modèle:Sfrac. De même, Modèle:Sfrac = Modèle:Sfrac et Modèle:Sfrac = Modèle:Sfrac.

Corollaire

On déduit de la loi des cotangentes une expression du rayon Modèle:Math du cercle inscrit, en fonction des longueurs des côtés (et de leur demi-somme Modèle:Math) :

$r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}.$

En effet, la somme des angles Modèle:Sfrac, Modèle:Sfrac et Modèle:Sfrac [[somme des angles d'un triangle|est égale à Modèle:Sfrac]] donc sa cotangente est nulle, c'est-à-dire (d'après la formule d'addition pour les cotangentes) que le produit et la somme des cotangentes de ces trois angles sont égaux, donc

$(p-a)(p-b)(p-c)=r^3\cot (\frac{\alpha }{2})\cot (\frac{\beta }{2})\cot (\frac{\gamma }{2})=r^3[\cot (\frac{\alpha }{2})+\cot (\frac{\beta }{2})+\cot (\frac{\gamma }{2})]=r^2[(p-a)+(p-b)+(p-c)]=r^{2}p,$

d'où l'expression annoncée.

Puisque (cf. Fig. 2) [[Cercles inscrit et exinscrits d'un triangle#Cercle inscrit|l'aire du triangle est Modèle:Math]], cette expression de Modèle:Math équivaut à la formule de Héron :

$S=\sqrt{p(p-a)(p-b)(p-c)}.$

Voir aussi

• Loi des cosinus
• Loi des sinus
• Loi des tangentes