Vecteur isotrope
En mathématiques, un vecteur isotrope pour une forme bilinéaire[1] f est un vecteur x tel que f(x, x) = 0.
Définitions
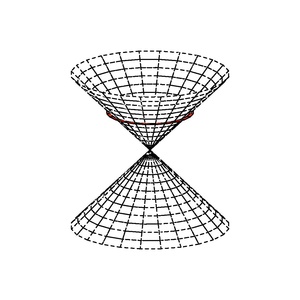
Soient E un espace vectoriel et f une forme bilinéaire symétrique sur E.
On dit qu'un vecteur x de E est isotrope (pour f[2]Modèle:,[3], ou pour la forme quadratique associée[4]) si f(x, x) = 0.
L'ensemble des vecteurs isotropes est appelé le cône isotrope. Il contient le noyau de f[4]. Au cône isotrope, on associe une quadrique projective.
La forme bilinéaire est dite définie[2] — et la forme quadratique est dite anisotrope[5] — si 0 est son seul vecteur isotrope.
Propriétés
- Lorsque E est un espace vectoriel réel, si f (symétrique) est définie alors f ou –f est définie positive, c'est-à-dire que c'est un produit scalaire.Modèle:Retrait
- Lorsque E est un espace vectoriel complexe de dimension supérieure ou égale à 2, f n'est jamais définie.Modèle:Retrait
Notes et références
- ↑ Plus précisément : bilinéaire symétrique ou antisymétrique. Modèle:Ouvrage.
- ↑ 2,0 et 2,1 Modèle:Ouvrage.
- ↑ Modèle:Ouvrage.
- ↑ 4,0 et 4,1 Modèle:Harvsp.
- ↑ Modèle:Ouvrage.