Dilatation (géométrie)

Dessin d'origine	Résultat de la dilatation

Cet article est à lire en parallèle avec celui sur les transvections.

Dilatation vectorielle

Une dilatation d'un espace vectoriel E est une affinité de base un hyperplan, et de rapport non nul.

Les dilatations sont bijectives. L'ensemble des dilatations de base et direction fixées forme un sous-groupe du groupe linéaire GL(E), isomorphe au groupe multiplicatif du corps de base.

En dimension finie, un automorphisme de E est diagonalisable si et seulement s'il est produit commutatif de dilatations ; si de plus le corps de base a au moins 3 éléments, GL(E) est engendré par les dilatations.

Matrice de dilatation

Dans une base de $E$ formée de vecteurs de la base et de la direction de la dilatation, la dilatation a pour matrice une matrice du type $\mathrm{diag}(1,1,..,1,\lambda ,1,..,1)=I_n+(\lambda -1)E_{ii}$. Ces matrices sont donc appelées matrices de dilatation.

Dilatation affine

Une dilatation d'un espace affine E est une affinité de base un hyperplan, et de rapport non nul ; ce sont les applications affines de partie linéaire une dilatation vectorielle, sauf dans le cas du rapport 1.

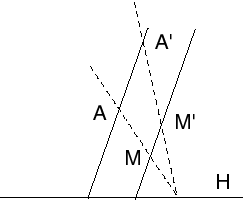
Étant donnés deux points A et AModèle:' et un hyperplan H non parallèle à la droite (AAModèle:'), il existe une unique dilatation de base H envoyant A sur AModèle:' ; on obtient facilement l'image MModèle:' d'un point M par la construction :

En dimension finie, et si le corps de base a au moins 3 éléments, le groupe affine GA(E) est engendré par les dilatations.

Dilatation projective

Si l'on plonge l'espace affine $E$ dans son complété projectif, en lui adjoignant un hyperplan à l'infini $H^{\prime }$, on sait que l'on peut munir le complémentaire $E^{\prime }$ de l'hyperplan $H$ d'une structure d'espace affine (les droites qui sont sécantes en un point de $H$ dans $E$ deviennent parallèles dans $E^{\prime }$ et celles qui sont parallèles dans $E$ deviennent sécantes en un point de $H^{\prime }$).

À toute dilatation d'hyperplan $H$ de $E$ est alors associée une application affine de $E^{\prime }$ qui n'est autre qu'une homothétie.

Les dilatations en perspective deviennent donc en fait des homothéties. Si l'on regarde par avion une dilatation de base parallèle à la ligne d'horizon, on voit une homothétie dont le centre est sur la ligne d'horizon :

Si maintenant on envoie un autre hyperplan que $H$ et $H^{\prime }$ à l'infini, la dilatation devient une homologie non spéciale.

En résumé, il y a, en géométrie projective, identité entre les homothéties, les dilatations, et les homologies non spéciales.

Dilatation orthogonale

Ce sont, dans le cas euclidien, les dilatations dont la base est orthogonale à la direction. Elles contiennent comme cas particulier les réflexions.

Réalisation d'une dilatation par perspective parallèle

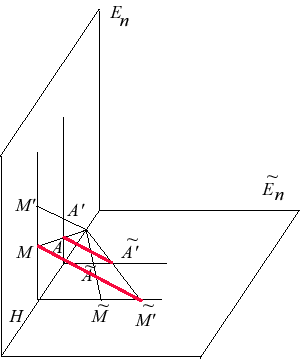
Plongeons l'espace euclidien $E_n$ de dimension n comme hyperplan d'un espace $E_{n+1}$ de dimension n+1 et faisons tourner $E_n$ autour de son hyperplan $H$, de façon à en obtenir une copie ${\tilde{E}}_n$.

Tout point $M$ de $E_n$ a une copie $\tilde{M}$ dans ${\tilde{E}}_n$, donc aussi l'image $M^{\prime }$ de $M$ par une dilatation de base $H$.

On montre que la droite $(M{\tilde{M}}^{\prime })$ garde une direction fixe $D$, ce qui montre que ${\tilde{M}}^{\prime }$ s'obtient par projection de $M$ dans $E_{n+1}$ (projection de base ${\tilde{E}}_n$ et de direction $D$).

Voir ici une réalisation concrète de ce procédé.

Annexes

Articles connexes

• Transformation
• Homologie

Référence

Source pour la partie projective : Alain Bigard, Géométrie, Cours et exercices corrigés pour le Capes et l'agrégation, Masson, 1998 Modèle:Portail