Finesse (aérodynamique)

Modèle:Voir homonymes La finesse est une caractéristique aérodynamique définie comme le rapport entre la portance et la traînée.

Elle est parfois désignée par le terme de langue anglaise Modèle:Citation signifiant Modèle:Citation étrangère, c'est-à-dire rapport portance/traînée en français.

On peut aussi définir de manière équivalente la finesse comme le rapport des coefficients de portance et de traînée $\frac{C_z}{C_x}$, à condition que ces deux coefficients soient rapportés à la même surface.

Définition

Schéma définissant assiette, incidence et pente.

La finesse d'un aérodyne à voilure fixe est le rapport entre sa portance et sa traînée aérodynamique. En vol plané (sans force de traction/propulsion) à vitesse vraie (vitesse de l'aéronef par rapport à la masse d'air dans laquelle il se déplace) constante, et donc à pente constante, elle est égale au rapport entre la distance horizontale parcourue et la hauteur de chute ou encore au rapport entre la vitesse horizontale et la vitesse verticale (taux de chute). Bien sûr, cette définition est à adapter suivant l'objet étudié : voile de bateau, profil de carène…

$\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}=\frac{P}{T}=\frac{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{u}\mathrm{e}}{\mathrm{h}\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{u}\mathrm{e}}=\frac{v_{\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{e}}}{v_{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}}$

Pour un aérodyne donné, la finesse varie en fonction de l'incidence de l'aile. Cependant, comme le coefficient de portance varie aussi avec l'angle d'incidence, pour obtenir une portance équivalente au poids, il faut adapter la vitesse. C'est pourquoi la finesse varie avec la vitesse.

Dans le cas d'un planeur, la finesse varie en fonction de la vitesse sur trajectoire en suivant une courbe qu'on appelle la polaire des vitesses.
Cette courbe représente le taux de chute en fonction de la vitesse sur trajectoire (ou « vitesse indiquée »). Elle est croissante entre la valeur de la vitesse de décrochage jusqu'à la valeur de la vitesse correspondant au taux de chute minimal, puis décroissante au-delà.

À vitesse constante, la $|\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}|=\arctan \left(\frac{1}{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}}\right)$

Par exemple, une finesse de 7 correspond à un angle de plané de ~8Modèle:Unité.

Valeurs typiques

Les avions ont généralement des finesses comprises entre 8 et 20 : les avions de ligne ont des finesses comprises entre 16 et 18, l'Airbus A320 a une finesse de 17, le Boeing 747 de 17,7. Le Concorde avait une finesse de 4 au décollage, 12 à Mach 0,95 et 7,5 à Mach 2

Les derniers prototypes de « wingsuit » permettent d'atteindre une finesse de 3. Les parapentes modernes ont une finesse comprise entre 9 et 13. Les deltaplanes « souples » modernes ont une finesse comprise entre 14 et 16, et les deltaplanes « rigides » modernes ont une finesse comprise entre 18 et 22. Les planeurs de construction en bois et toile de 27 à 32 et les planeurs plastiques ont commencé à 30 et sont à plus de 60 actuellement.

Typiquement, sur un planeur moderne :

• la vitesse de finesse maximale se situe entre 80 et Modèle:Unité selon le modèle et la charge alaireModèle:, ;
• la vitesse de taux de chute minimal est de l'ordre de Modèle:Unité et le taux de chute correspondant de l'ordre de 0,8 à Modèle:Unité ;
• la vitesse de décrochage est de l'ordre de Modèle:Unité.

Un avion à propulsion humaine permettant de voler en pédalant a un meilleur rapport portance/traînée de 30.

Équivalence entre les définitions

Forces en vol plané

Système : avion

Référentiel : terrestre supposé galiléen

Bilan des forces extérieures au système :

• Portance ${\overrightarrow{F}}_z$ perpendiculaire à la vitesse de déplacement de l'avion
• Traînée ${\overrightarrow{F}}_x$ opposée à la vitesse de déplacement de l'avion
• Poids $m\overrightarrow{g}$

D'après la deuxième loi de Newton on a :

$m\frac{d\overrightarrow{V}}{dt}={\overrightarrow{F}}_x+\overrightarrow{F_z}+m\overrightarrow{g}$

On suppose que l'aéronef est en mouvement non accéléré et l'on a donc :

$\overrightarrow{0}=m\frac{d\overrightarrow{V}}{dt}={\overrightarrow{F}}_x+\overrightarrow{F_z}+m\overrightarrow{g}$

Soient C_z le coefficient de portance et C_x le coefficient de traînée. On note que le coefficient de portance est en première approximation proportionnel à l'angle d'incidence.

Cela se traduit donc en projetant sur chacun des axes par :

• sur Ox : $0=-\frac{1}{2}\rho V^{2}S{C}_x+mg\sin \gamma$
• sur Oz : $0=\frac{1}{2}\rho V^{2}S{C}_z-mg\cos \gamma$

Et donc, pour un vol plané à vitesse vraie constante :

$\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}=\frac{1}{\tan |\gamma |}=\frac{\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{u}\mathrm{e}}{\mathrm{h}\mathrm{a}\mathrm{u}\mathrm{t}\mathrm{e}\mathrm{u}\mathrm{r}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{d}\mathrm{u}\mathrm{e}}=\frac{v_{horizontale}}{v_{verticale}}$

Et donc :

$f=\frac{1}{\tan \gamma }=\frac{C_z}{C_x}$

Pour un planeur, on pourra aisément écrire que $\tan \gamma \approx \gamma$ (si $\gamma$ est exprimé en radians). Cependant cela ne sera pas correct pour un wingsuit qu'on pourrait presque assimiler à un « fer à repasser ».

Finesse air et finesse sol

La finesse air d'un aéronef est donnée par rapport à la masse d'air dans laquelle il se déplace. C'est souvent celle que le constructeur annonce car elle est indépendante du vent.

La finesse sol, elle, est calculée par rapport au sol. C'est souvent la plus intéressante car c'est celle qui détermine si un parcours jusqu'à un but est possible ou non. Cette finesse doit tenir compte du déplacement de l'air (du vent) par rapport au sol.

Quand l'aéronef se déplace dans la direction et le sens du vent, la finesse sol augmente, et inversement s'il se déplace dans le sens inverse. Par vent fort de face, l'aéronef peut avoir une vitesse sol et une finesse sol faibles ou négatives, ce qui sera d'ailleurs souvent une raison suffisante pour annuler le vol.

La finesse air et la finesse sol sont égales lorsque l'air est calme et ne subit aucun mouvement vertical ni horizontal.

Calcul de la finesse maximale

Relation entre la traînée induite et la traînée parasite

Courbes montrant les trainée induite, parasite ainsi que la trainée combinée par rapport à la vitesse de l'air

On va montrer qu'un aéronef atteint sa finesse maximale lorsque la traînée induite est égale à la traînée parasite.

La traînée parasite $R_{\mathrm{p}}$ causée par la résistance de l'air peut s'écrire sous la forme

$R_{\mathrm{p}}=qS{C}_{x,\mathrm{p}}$

où $C_{xp}$ est le coefficient de traînée parasite et on a $C_{xp}=cte$. Soit $b$ l'envergure de l'aile et $c$ sa corde moyenne (~ largeur moyenne de l'aile). $q=\frac{1}{2}\rho V^2$ est la pression dynamique.

On pose $\lambda =\frac{b}{c}$ l'allongement de l'aile. On rappelle que $S=\frac{b^2}{\lambda }$

On note $\rho$ la masse volumique de l'air. On obtient :

$R_{\mathrm{p}}=\frac{1}{2}\rho V^{2}S{C}_{x,\mathrm{p}}=\frac{1}{2}\frac{\rho b^2{V}^2{C}_{x,\mathrm{p}}}{\lambda }$

La traînée induite $R_{\mathrm{i}}$ s'exprime comme suit :

$R_{\mathrm{i}}=2\frac{F_z^2}{b^2\rho V^2\pi e}=\frac{1}{2}\rho V^{2}S{C}_{x,\mathrm{i}}$ avec $C_{x,\mathrm{i}}=\frac{C_z^2}{\lambda \pi e}$

où $F_z$ est la portance, $V$ est la vitesse de l'aéronef et $e$ est le coefficient d'Oswald. Cette dernière formule provient de la théorie des profils minces.

Lorsqu'un avion ou planeur est en vol, la traînée induite $R_{\mathrm{i}}(V)$ et la traînée parasite $R_{\mathrm{p}}(V)$ s'ajoutent et constituent la traînée totale :

$R(V)=\frac{1}{2}\rho V^{2}S{C}_x$ avec $C_x=C_{x,\mathrm{p}}+C_{x,\mathrm{i}}$

Pour ne pas alourdir les calculs avec des racines carrés dans la suite on exprimera non pas la finesse $f$, mais la finesse au carré et on a alors :

$f^2=\frac{C_z^2}{C_x^2}=\frac{\lambda \pi e{C}_{x,\mathrm{i}}}{C_x^2}=\lambda \pi e\frac{C_x-C_{x,\mathrm{p}}}{C_x^2}$

On dérive par rapport à $C_x$ :

$2f\frac{df}{d{C}_x}=\lambda \pi e\frac{-C_x^2+2C_{x,\mathrm{p}}{C}_x}{C_x^4}$

Pour que $f$ soit maximale il faut que $\frac{df}{d{C}_x}=0$ ce qui revient ici à déterminer les racines d'un polynôme du second degré en $C_x$.

On obtient donc que $f_{\mathrm{m}\mathrm{a}\mathrm{x}}$ est atteinte quand $C_x=2C_{x,\mathrm{p}}$ c'est-à-dire :

$C_{x,\mathrm{p}}=C_{x,\mathrm{i}}$ et donc $R_{\mathrm{p}}=R_{\mathrm{i}}$

Ce qui signifie que la traînée induite est égale à la traînée parasite.

Démonstration simplifiée pour un planeur

Tout ce qui suit appliqué aux planeurs a été présenté dans l'ouvrage de Frank Irving The Paths of Soaring Flight.

Dans les cours d'aérodynamique pour pilotes, il est souvent affirmé sans justification que la traînée induite est proportionnelle à 1/VModèle:2 et que la traînée parasite est proportionnelle à VModèle:2. Dans ces conditions, la démonstration du théorème ci-dessus devient triviale qui est alors un simple corollaire des postulats énoncés ci-dessus. Dans ce qui suit, les postulats vont être démontrés et l'on va en conclure le théorème ci-dessus.

Les planeurs ont des angles de plané qui sont très petits et l'on peut donc supposer que $F_z=mg$

La traînée induite $R_{\mathrm{i}}$ s'exprime comme suit :

$R_i=2\frac{F_z^2}{b^2\rho V^2\pi e}=2\frac{m^2{g}^2}{b^2\rho V^2\pi e}$

La traînée parasite $R_{\mathrm{p}}$ causée par la résistance de l'air peut s'écrire sous la forme

$R_{\mathrm{p}}=\frac{1}{2}\rho V^{2}S{C}_{x,\mathrm{p}}=\frac{1}{2}\frac{\rho b^2{V}^2{C}_{x,\mathrm{p}}}{\lambda }$

Lorsqu'un planeur est en vol, la traînée induite $R_{\mathrm{i}}(V)$ et la traînée parasite $R_{\mathrm{p}}(V)$ s'ajoutent et constituent la traînée totale R(V). La finesse d'un planeur sera optimale lorsque la traînée totale R(V) est minimale. On résout donc l'équation

$\frac{\mathrm{d}R(V)}{\mathrm{d}V}=0$

On définit $\alpha$ et $\beta$ tels que $\alpha =\frac{1}{2}\frac{\rho b^2{C}_{x,\mathrm{p}}}{\lambda }$ et $\beta =\frac{2m^2{g}^2}{b^2\rho \pi e}$. On peut écrire symboliquement :

$R_{\mathrm{p}}(V)=\alpha V^2{R}_{\mathrm{i}}(V)=\frac{\beta }{V^2}$

Après avoir calculé la dérivée de R(V), on résout donc :

$2\alpha V-2\frac{\beta }{V^3}=0$

Et donc en multipliant la relation ci-dessus par V, on obtient :

$\alpha V^2=\frac{\beta }{V^2}$

ce qui signifie que la traînée induite est égale à la traînée parasite.

Vitesse optimale

On pose $\alpha =\frac{1}{2}\frac{\rho b^2{C}_{x,\mathrm{p}}}{\lambda }$ et $\beta =\frac{2F_z^2}{b^2\rho \pi e}$. On a alors :

$R_p(V)=\alpha V^2{R}_i(V)=\frac{\beta }{V^2}$

Le planeur atteindra sa finesse maximale en air calme lorsque la traînée induite sera égale à la traînée parasite, c'est-à-dire :

$\alpha V^2=\frac{\beta }{V^2}$

$V_f={\left(\frac{\beta }{\alpha }\right)}^{\frac{1}{4}}=\frac{\sqrt{2}}{(\pi e{)}^{\frac{1}{4}}b}\times \sqrt{\frac{F_z}{\rho }}\times {\left(\frac{\lambda }{C_{x,\mathrm{p}}}\right)}^{\frac{1}{4}}$

Détermination des coefficients de traînée et d'Oswald

Si l'on connaît la vitesse à laquelle la finesse maximale est connue, on peut en déduire le coefficient de traînée parasite et le coefficient d'Oswald. Ces coefficients valent :

$C_{x,\mathrm{p}}=\frac{P}{f\rho V_f^2}$

$e=\frac{4fP}{\pi \lambda \rho V_f^2}$

P est la charge alaire et λ est l'allongement de l'aile. Modèle:Boîte déroulante

Calcul de la finesse maximale (d'un planeur)

Schéma des forces appliquées sur un planeur en vol rectiligne uniforme.

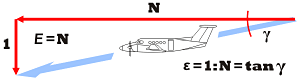
Un planeur n'a pas de moteur ; il est « propulsé » par la composante sur trajectoire de son propre poids (voir le schéma ci-contre).

Soit f(V) la finesse du planeur défini par le rapport de la vitesse horizontale à la vitesse verticale. Soit $\gamma$ l'angle de plané en radians. Comme $\gamma$ est petit, on peut écrire que $\gamma \approx \tan \gamma$ et donc que :

$\gamma \approx \frac{1}{f(V)}$

Quand le planeur est en équilibre, en mouvement non accéléré, on a :

$R(V)=\tan (\gamma F_z)\approx \gamma F_z$

De plus, la finesse maximale est une caractéristique de l'aéronef et est donc constante (tant que les caractéristiques de l'aéronef sont inchangées).

Dans ce qui suit, on démontre cette assertion qui ne semble pas évidente. On rappelle que lorsque la planeur atteint sa finesse maximale la traînée induite est égale à la traînée parasite. On obtient donc :

$\gamma =\frac{R_i(V)+R_p(V)}{F_z}=\frac{2R_p(V)}{F_z}=\frac{\rho C_{x,\mathrm{p}}{b}^2{V}^2}{\lambda F_z}=\frac{\rho C_{x,\mathrm{p}}{b}^2}{\lambda F_z}\times {(\frac{\sqrt{2}}{(\pi e{)}^{\frac{1}{4}}b}\times \sqrt{\frac{F_z}{\rho }}\times {\left(\frac{\lambda }{C_{x,\mathrm{p}}}\right)}^{\frac{1}{4}})}^2$

Et donc :

$\gamma =2\sqrt{\frac{C_{x,\mathrm{p}}}{\lambda \pi e}}$

Et donc :

$\frac{1}{\gamma }=f=\frac{1}{2}\sqrt{\frac{\lambda \pi e}{C_{x,\mathrm{p}}}}$

Comme annoncé ci-dessus, la finesse maximale ne dépend pas de la masse du planeur et ni de la densité de l'air environnant. Elle dépend uniquement de l'aérodynamisme du planeur et de sa géométrie (allongement) : la finesse maximale est une caractéristique de l'aéronef et est donc constante. Ceci justifie a posteriori que la vitesse de chute du planeur augmentera en même temps que sa masse. Donc, lorsque les conditions aérologiques sont moins favorables, il est préférable de minimiser la masse du planeur pour minimiser la vitesse de chute et donc de ne pas ajouter d'eau dans les ailes ou, si l'on est déjà en vol, de vidanger les ailes.

De plus, plus $\lambda$ est grand, plus $\gamma \approx \tan \gamma$ sera petit. Donc, les planeurs ayant des grandes ailes, pour une surface alaire équivalente, aura un plus petit angle de plané et donc une plus grande finesse. Ceci est la raison pour laquelle certains planeurs de compétition en classe libre peuvent avoir jusqu'à Modèle:Unité d'envergure.

Effet de la masse sur la vitesse optimale

Cette section suppose que l'aéronef a une finesse suffisante pour que l'on puisse supposer que $\gamma \approx \tan \gamma$.

On considère un planeur de masse $m$ volant à sa vitesse de finesse maximale $V_1$. Le poids du planeur est donné par $\cos \gamma F_z=mg$. Pour simplifier la discussion, on suppose que $\cos \gamma \approx 1$. On a donc :

$C_{x,\mathrm{p}}=\frac{4}{\lambda \pi e}\frac{m^2{g}^2}{{\rho }^2{S}^2{V_1}^4}$

On considère maintenant le même planeur auquel on a ajouté de l'eau et qui a une masse $M$ et une vitesse de finesse maximale $V_2$. On a alors :

$\frac{4}{\lambda \pi e}\frac{m^2{g}^2}{{\rho }^2{S}^2{V_1}^4}=C_{x,\mathrm{p}}=\frac{4}{\lambda \pi e}\frac{M^2{g}^2}{{\rho }^2{S}^2{V_2}^4}$

Donc,

$\frac{m^2}{{V_1}^4}=\frac{M^2}{{V_2}^4}$

Donc,

${\left(\frac{V_2}{V_1}\right)}^4={\left(\frac{M}{m}\right)}^2$

et donc :

$\frac{V_2}{V_1}=\sqrt{\frac{M}{m}}$.

On constate que la vitesse optimale varie donc comme la racine carrée de la masse du planeur.

En augmentant la masse, on augmente donc aussi la vitesse de finesse maximale mais la valeur de la finesse maximale elle reste constante. La finesse maximale étant indépendante de la masse de l'aéronef, ceci signifie que le même planeur auquel on ajoute de l'eau aura la même portée, mais volera plus vite pour maintenir la même portée. C'est pourquoi lorsque les conditions météorologiques sont très favorables (puissantes ascendances), les planeurs de compétition sont remplis d'eau dans les ailes.

Polaire des vitesses

La polaire des vitesses peut se mettre sous la forme :

$V_z=A{V}^3+B\frac{1}{V}$

où A et B sont des constantes à déterminer.

On évalue maintenant la vitesse de chute en fonction de la vitesse horizontale pour n'importe quelle vitesse. On a :

$\tan \gamma =\frac{R_i(V)+R_p(V)}{F_z}=\frac{2F_z}{b^2\rho V^2\pi e}+\frac{\rho C_{x,\mathrm{p}}{b}^2{V}^2}{2\lambda F_z}$

La polaire des vitesses exprime la vitesse de chute $V_z$ en fonction de la vitesse horizontale. Etant donné que $\gamma$ est très petit, on a : $\tan \gamma \approx \gamma$

On peut donc considérer que $V_z=\gamma V$. Donc,

$V_z=(\frac{2F_z}{b^2\rho V^2\pi e}+\frac{\rho C_{x,\mathrm{p}}{b}^2{V}^2}{2\lambda F_z})V$

Cette formule exprime la polaire des vitesses. On constate que pour $V$ grand, la finesse décroît comme le carré de la vitesse horizontale.

On notera que $\frac{F_z\lambda }{b^2}$ est la charge alaire qui est souvent exprimée en Modèle:Nb ou plus incorrectement en Modèle:Nb. Si l'on appelle P cette charge alaire (qui est homogène à une pression), on obtient :

$V_z=(\frac{P}{\rho V^2\lambda \pi e}+\frac{\rho C_{x,\mathrm{p}}{V}^2}{2P})V$

et donc :

$A=\frac{\rho C_{x,\mathrm{p}}}{2P}B=\frac{P}{\rho \lambda \pi e}$

Vitesse de chute à finesse maximale

On a :

$V_{z,f}=(\frac{\alpha }{V_f^2}+\beta V_f^2)\frac{V_f}{F_z}$

Comme $\alpha /V^2=\beta V^2$ à finesse maximale, on obtient donc :

$V_{z,f}=2\beta V_f^2\frac{V_f}{F_z}$

En substituant β, on obtient

$V_{z,f}=\rho \frac{C_{x,\mathrm{p}}}{\lambda }{b}^2\frac{V_f^3}{F_z}$

On remplace Vf et donc,

$V_{z,f}=\rho \frac{C_{x,\mathrm{p}}}{\lambda }\frac{b^2}{F_z}{[\frac{\sqrt{2}}{(\pi e{)}^{\frac{1}{4}}b}\times \sqrt{\frac{F_z}{\rho }}\times {\left(\frac{\lambda }{C_{x,\mathrm{p}}}\right)}^{\frac{1}{4}}]}^3={\left(\frac{C_{x,\mathrm{p}}}{\lambda }\right)}^{\frac{1}{4}}\frac{2\sqrt{2}}{(\pi e{)}^{\frac{3}{4}}}\frac{1}{b}\sqrt{\frac{F_z}{\rho }}$

On note que :

$C_{x,\mathrm{p}}=\frac{\lambda \pi e}{4f^2}$

En substituant, on obtient :

$V_{z,f}={\left(\frac{\pi e}{4f^2}\right)}^{\frac{1}{4}}\frac{2\sqrt{2}}{(\pi e{)}^{\frac{3}{4}}}\frac{1}{b}\sqrt{\frac{F_z}{\rho }}=\frac{2}{b}\sqrt{\frac{F_z}{f\pi e\rho }}$

Vitesse de chute minimum

En reprenant les notations ci-dessus, on a :

$V_z=\frac{\alpha }{F_{z}V}+\frac{\beta V^3}{F_z}$

On appelle vitesse minimale $V_m$ la vitesse horizontale pour laquelle le taux de chute minimal est atteint. Elle est atteinte lorsque $\frac{d{V}_z}{dV}=0$. On obtient donc :

$-\frac{\alpha }{F_z{V}_m^2}+3\frac{\beta V_m^2}{F_z}=0$

Soit $V_f$ la vitesse à finesse maximale. Donc,

$V_m={\left(\frac{\alpha }{3\beta }\right)}^{\frac{1}{4}}={\left(\frac{1}{3}\right)}^{\frac{1}{4}}{V}_f$

On obtient donc :

$V_m\approx 0.76\times V_f$

On a :

$V_{z,m}=(\frac{\alpha }{V_m^2}+\beta V_m^2)\frac{V_m}{F_z}$

On a $V_m={\left(\frac{\alpha }{3\beta }\right)}^{\frac{1}{4}}$ et donc $V_m^2=\sqrt{\frac{\alpha }{3\beta }}$ que l'on substitue et donc,

$V_{z,m}=\frac{V_m}{F_z}(\frac{\alpha }{\sqrt{\frac{\alpha }{3\beta }}}+\beta \sqrt{\frac{\alpha }{3\beta }})=\frac{V_m}{F_z}\sqrt{\alpha \beta }(\sqrt{3}+\frac{1}{\sqrt{3}})$

On substitue V_m et donc,

$V_{z,m}=\frac{1}{F_z}{\left(\frac{\alpha }{3\beta }\right)}^{\frac{1}{4}}\sqrt{\alpha \beta }\frac{4}{\sqrt{3}}=\frac{{\alpha }^{\frac{3}{4}}{\beta }^{\frac{1}{4}}}{3^{\frac{1}{4}}}\times \frac{1}{F_z}\times \frac{4}{\sqrt{3}}$

On substitue maintenant α et β et donc,

$V_{z,m}={\left(\frac{2F_z^2}{b^2\rho \pi e}\right)}^{\frac{3}{4}}{\left(\frac{1}{2}\frac{\rho b^2{C}_{x,\mathrm{p}}}{\lambda }\right)}^{\frac{1}{4}}\frac{1}{3^{\frac{1}{4}}}\times \frac{1}{F_z}\times \frac{4}{\sqrt{3}}$

On obtient donc :

$V_{z,m}=\frac{4\sqrt{2}}{3^{\frac{3}{4}}}\frac{1}{(\pi e{)}^{\frac{3}{4}}}{\left(\frac{C_{x,\mathrm{p}}}{\lambda }\right)}^{\frac{1}{4}}\frac{1}{b}\sqrt{\frac{F_z}{\rho }}$

Le rapport entre la vitesse de chute minimale et la vitesse de chute à finesse maximale est :

$\frac{V_{z,m}}{V_{z,f}}=\frac{\frac{4\sqrt{2}}{\sqrt{3}b}\frac{1}{(\pi e{)}^{\frac{3}{4}}}{\left(\frac{C_{x,\mathrm{p}}}{\lambda }\right)}^{\frac{1}{4}}\frac{1}{b}\sqrt{\frac{F_z}{\rho }}}{{\left(\frac{C_{x,\mathrm{p}}}{\lambda }\right)}^{\frac{1}{4}}\frac{2\sqrt{2}}{(\pi e{)}^{\frac{3}{4}}}\frac{1}{b}\sqrt{\frac{F_z}{\rho }}}=\frac{4\sqrt{2}}{3^{\frac{3}{4}}}\times \frac{1}{2\sqrt{2}}=\frac{2}{3^{\frac{3}{4}}}\approx 0.88$

On constate donc que la vitesse de chute minimale n'est que 12 % inférieure à la vitesse de chute à finesse maximale.

Application au planeur ASW 27

On considère le planeur Alexander Schleicher ASW 27.

Le constructeur affirme que son planeur a une finesse de 48. Les chiffres officiels sont les suivants :

• λ = 25 ;
• e = 0,85 ;
• b = Modèle:Unité ;
• C_x,p = 0,0072 (ajusté pour satisfaire la finesse déclarée).

On obtient alors :

$\frac{1}{\gamma }=\frac{1}{2}\sqrt{\frac{25\times \pi \times 0,85}{0,0072}}=48,1$

La masse à vide du planeur est 245 kilogrammes. On considère un pilote de masse 65 kilogrammes volant aux conditions normales de température et de pression. On a alors :

• ρ = 1,225 ;
• m = Modèle:Unité.

La vitesse à laquelle la finesse maximale est atteinte est

$V_m=\frac{\sqrt{2}}{(\pi \times 0,85{)}^{\frac{1}{4}}\times 15}\times \sqrt{\frac{310\times 9,8}{1,225}}\times {\left(\frac{25}{0,0072}\right)}^{\frac{1}{4}}=28,19\mathrm{m}/\mathrm{s}=101,5\mathrm{k}\mathrm{m}/\mathrm{h}$

Le constructeur affirme que la finesse maximale est atteinte à Modèle:Unité ce qui fait que le modèle n'engendre une erreur que de moins de 2 %.

Donc, la vitesse horizontale de chute minimale sera.

$V_m=98,7\times 0,76=77\mathrm{k}\mathrm{m}/\mathrm{h}$

En examinant la polaire des vitesses, on constate que la vitesse de chute minimum est à Modèle:Unité ce qui correspond donc à la formule ci-dessus.

Le taux de chute minimal est

$V_{z,m}=\frac{28,19}{48}\times 0,88=0,52$

Le constructeur affirme que le taux de chute minimal est Modèle:Unité.

On constate que dans le cas du planeur ASW-27, la théorie des profils minces peut représenter la polaire des vitesses et les caractéristiques du planeur à moins de 2 % près.

Autres domaines

• Une voile est aussi un profil. La notion de finesse s'applique donc aussi à ce profil, mais de plusieurs façons. Voir finesse d'une voile de bateau.

• Une hélice aquatique est composée de plusieurs pales, chacune ayant un profil. La définition de finesse est identique à la finesse aérodynamique, le fluide étant de l'eau.

Généralisation de la notion de finesse à tous les modes de transport

Mise à jour 2004 du diagramme de Gabrielli-von Karman donnant la finesse « totale » des différents modes de transport.

Plus généralement, la notion de finesse peut s'appliquer avantageusement à tous les modes de transport (de marchandise ou de passagers) pour permettre l'évaluation de leur rendement énergétique. En effet, le rendement de chaque véhicule est le quotient du poids de ce véhicule sur les forces de traînée qui le freinent (diagramme de Gabrielli-von Kármán ci-contre). En dressant ce diagramme, après avoir pris acte de l'impossibilité de mesurer la valeur que chaque homme accorde à la vitesse de ses déplacements, Karman et Gabrielli ont posé les fondations d'un système de mesure de l'économie des déplacements (de marchandise ou d'humains), ce système de mesure demeurant valide plus de 70 ans après sa création.

Pour un vélo, par exemple, dont le coefficient de résistance au roulement va de 0,0022 à 0,005, la finesse à basse vitesse ira de $\frac{1}{0,0022}$ (soit 454) à 200 (si la traînée aérodynamique est négligée). Autre exemple : Pour une berline la traînée est la somme de sa traînée aérodynamique et de sa résistance au roulement)Modèle:,. Le coefficient de résistance au roulement des meilleurs pneumatiques pour berlines s'abaisse jusqu'à 0,006. La finesse d'une telle berline en ville est donc plus faible que $\frac{1}{0,006}$, soit 166. Cependant, il suffit de pousser un tel véhicule pour constater que, malgré cette excellente finesse, la traînée de roulement est très forte (donc la perte d'énergie par roulement très forte également). Cela suffit à suggérer que la finesse ne soit plus définie comme le quotient du poids du véhicule sur sa force de traînée mais comme le quotient du poids de ses passagers sur la force de traînée que le déplacement suscite (la traînée du véhicule), soit pour deux passagers (Modèle:Unité avec les bagages) dans l'exemple ci-dessus (c.-à-d. à basse vitesse) une finesse de simplement 33,3 (et 16,7 pour le conducteur seul).
Il manque donc au travail de collecte de données par Gabrielli et von Karman une évaluation efficace de l'énergie nécessaire pour déplacer le véhicule lui-même et de l'énergie nécessaire pour déplacer la charge utile. En effet, les deux auteurs n’ont pu recueillir la charge utile ni la vitesse de croisière des véhicules étudiés. De fait, ce graphe n’accorde pas d’avantage à l’emport accru de fret ou de passagers en ceci qu’un véhicule mal conçu dont la structure serait Modèle:Unité trop lourde et qui, pour compenser ce surpoids, emporterait 10 passagers de moins (avec leur bagages) aurait la même finesse généralisée sur le graphe ci-contre qu’un véhicule mieux conçu et emportant 10 passagers de plus (sur ce point, le diagramme de la finesse commerciale, d’après Papanikolaou, pourrait constituer un progrès).

Articles connexes

• Effort sur une voile
• Vitesse de vol optimale en vol à voile
• Diagramme de Gabrielli – von Kármán
• Efficacité énergétique dans les transports

Bibliographie

• Modèle:Ouvrage
• Modèle:Ouvrage.