Formule de Rydberg

La formule de Rydberg comme elle apparaît dans un manuscrit de Modèle:Date-.

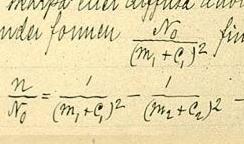
En physique atomique, la formule de Rydberg permet de calculer les longueurs d'onde des raies spectrales de nombreux éléments chimiques. Elle fut établie empiriquement en 1888 par le physicien suédois Johannes Rydberg à partir des raies spectrales des métaux alcalins et de la formule de Balmer, établie par Johann Jakob Balmer en 1885, pour les raies du spectre visible de l'hydrogène. Sous sa forme la plus simple, elle est une généralisation de la formule de Balmer pour toutes les transitions de l'hydrogène. La formule de Rydberg fut exploitée en 1913 par le physicien danois Niels Bohr, pour élaborer son modèle de l'atome d'hydrogène à l'origine de la mécanique quantique.

Formule de Rydberg pour l'hydrogène

Dans la formule manuscrite apparaissant sur l'image :

$\frac{n}{N_0}=\frac{1}{(m_1+c_1{)}^2}-\frac{1}{(m_2+c_2{)}^2}$.

Rydberg désignait :

• par $n$, le nombre d'oscillations par mètre, soit la fréquence spatiale ;
• par $N_0$, la constante de nombre d'oscillations ;
• par $m_1$ et $m_2$, des entiers avec $m_2>m_1$ ;
• par $c_1$ et $c_2$, des nombres $<1$.

Il est apparu que, pour l'atome d'hydrogène, les coefficients $c_1$ et $c_2$ sont nuls. Il pouvait donc ré-écrire la formule

$n=N_0(\frac{1}{m_1^2}-\frac{1}{m_2^2})$.

En nommant $\sigma$ la fréquence spatiale dans le vide de la raie, en changeant $m_1$ et $m_2$ par $n_1$ et $n_2$ et en remplaçant le symbole $N_0$ de la constante par $R_{\text{H}}$, la constante de Rydberg de l'hydrogène, la formule devient :

$\sigma =\frac{1}{\lambda }=R_{\text{H}}(\frac{1}{n_1^2}-\frac{1}{n_2^2})$

où :

• $\lambda$ est la longueur d'onde de la raie dans le vide ;
• $n_1$ et $n_2$ sont des entiers tels que $n_2>n_1$ ;
• $R_{\text{H}}$ est la constante de Rydberg de l'hydrogène, qui vaut environ Modèle:Nb.

Les différents coefficients $n_1$ donnent naissance à différentes séries de raies spectrales lorsque le coefficient $n_2$ varie de $n_1+1$ à l'infini.

Pour chaque série, les valeurs limites de $\sigma$ et de $\lambda$ sont égales à :

${\sigma }_{n_1,\mathrm{\infty }}=\frac{R_{\text{H}}}{n_1^2}$ et ${\lambda }_{n_1,\mathrm{\infty }}=\frac{n_1^2}{R_{\text{H}}}$.

Tableau des séries de raies de l'hydrogène

$n_1$	$n_2$	Nom	${\lambda }_{n_2}$ (Modèle:Nb)	${\lambda }_{\mathrm{\infty }}$ (Modèle:Nb)	Domaine
1	$2\to \mathrm{\infty }$	Série de Lyman	121	91	UV
2	$3\to \mathrm{\infty }$	Série de Balmer	656	365	visible
3	$4\to \mathrm{\infty }$	Série de Paschen	1 874	820	IR
4	$5\to \mathrm{\infty }$	Série de Brackett	4 052	1 458	IR
5	$6\to \mathrm{\infty }$	Série de Pfund	7 476	2 278	IR
6	$7\to \mathrm{\infty }$	Série de Humphreys	12 368	3 280	IR

Généralisation aux hydrogénoïdes

La formule ci-dessus peut être généralisée à tout ion hydrogénoïde, c'est-à-dire ne possédant qu'un unique électron. Les cations He⁺, Li²⁺, Be³⁺ en sont des exemples.

$\sigma =\frac{1}{\lambda }=R_M\times (\frac{1}{n_1^2}-\frac{1}{n_2^2})$

où :

• $n_1$, numéro de la série, et $n_2$, numéro de la raie dans la série, sont des entiers tels que $n_2>n_1$ ;
• $R_M$ est la constante de Rydberg de l'atome.

$R_M=\frac{Z^2{R}_{\mathrm{\infty }}}{1+\frac{m_e}{M}}$

où :

• $Z$ est le numéro atomique ;
• $M$ est la masse atomique de l'élément ;
• $m_e$ est la masse de l'électron.

N. B. : Il apparaît que cette formule de Rydberg est celle d'une famille d'hyperboles, $n_1$ et $n_2$ définissant les positions respectives des sommets et des foyers. Ces hyperboles sont des franges d'interférences produites entre les ondes émises par le proton et par l'électron. Comme l'atome d'hydrogène n'a qu'un proton et qu'un électron, la représentation graphique des interférences est simple et claire ; pour les autres atomes, à l'exception des hydrogénoïdes, le modèle devient plus brouillé.

Articles connexes

• Constante de Rydberg
• Johannes Rydberg
• Walther Ritz