Isotropie transverse

L'isotropie transverse caractérise un matériau dont les propriétés présentent une symétrie de rotation. Le matériau présente une direction « privilégiée », et les propriétés (mécaniques, thermique, diélectriques...) selon cette direction sont différentes des propriétés en fonction d'une direction perpendiculaire à elle. En revanche, elle sont constantes dans le plan normal à cette direction.
Conséquences sur le tenseur d'élasticité
L'écriture de la loi de Hooke est simplifiée par cette propriété. En considérant qu'on a choisi (arbitrairement) de placer le repère tel que l'axe 1 (ou x) corresponde à la direction privilégiée du matériau, on a certaines relations entre les termes du tenseur des constantes élastiques. Les directions 2 et 3 (ou y et z) sont équivalentes, d'où[1] :
D'autre part, on a , conséquence de l'isotropie dans le plan. Le tenseur est donc entièrement caractérisé par 5 propriétés indépendantes.
Galerie
-
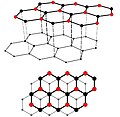
Structure cristalline du graphite
-
La structure mésoscopique du bois la donne une isotropie transverse approximative[3].
-
La glare est un matériau composite isotrope transverse utilisé en aéronautique[4].
![La structure feuilletée du schiste lui confère une isotropie transverse[2].](https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/%E9%A1%B5%E5%B2%A9.jpg/120px-%E9%A1%B5%E5%B2%A9.jpg)
![La structure mésoscopique du bois la donne une isotropie transverse approximative[3].](https://upload.wikimedia.org/wikipedia/commons/thumb/e/e5/Wood_fibers_100X.jpg/120px-Wood_fibers_100X.jpg)
![La glare est un matériau composite isotrope transverse utilisé en aéronautique[4].](https://upload.wikimedia.org/wikipedia/commons/thumb/b/ba/An_exploded_view_of_a_GLARE_hybrid_sheet.jpg/120px-An_exploded_view_of_a_GLARE_hybrid_sheet.jpg)