Modélisation en Pi des lignes électriques

Modèle en Pi d'une ligne électrique

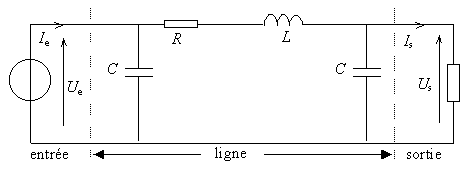
La modélisation en Pi des lignes électriques permet de représenter le comportement électrique attendu de celles-ci. Elle est basée sur les équations des télégraphistes. Le calcul des paramètres électriques utilisé pour la modélisation repose sur les équations de Maxwell. Le modèle avec une seule section en Pi n'est valable que pour de faibles fréquences et des lignes électriques courtes, dans le cas contraire plusieurs sections en Pi doivent être connectées en série.

Équations des télégraphistes

Représentation schématique des composants élémentaires d'une ligne de transmission.

Une portion de ligne électrique peut être représentée par le quadripole ci-contre où

• La résistance linéique (par unité de longueur) $R$ du conducteur est représentée par une résistance série (exprimée en ohms par unité de longueur).
• L'inductance linéique $L$ est représentée par une self (Henry par unité de longueur).
• La capacité linéique $C$ entre les 2 conducteurs est représentée par un condensateur C shunt (Farad par unité de longueur).
• La conductance linéique $G$ du milieu diélectrique séparant les 2 conducteurs est représentée par une résistance shunt (Siemens par unité de longueur). La résistance dans ce modèle a une valeur de $1/G$ ohms.

Dans ce modèle, on définit la tension en tout point éloigné d'une distance x du début de la ligne et à tout instant t la tension $U(x,t)$ et le courant $I(x,t)$. Les équations s'écrivent :

$\frac{\partial U}{\partial x}(x,t)=-L\frac{\partial I}{\partial t}(x,t)-RI(x,t)$

$\frac{\partial I}{\partial x}(x,t)=-C\frac{\partial U}{\partial t}(x,t)-GU(x,t)$

De la formulation ci-dessus, on peut tirer 2 équations aux dérivées partielles ne faisant chacune intervenir qu'une variable :

$\frac{{\partial }^{2}U}{\partial x^2}(x,t)=LC\frac{{\partial }^{2}U}{\partial t^2}(x,t)+(RC+GL)\frac{\partial U}{\partial t}(x,t)+GRU(x,t)$

$\frac{{\partial }^{2}I}{\partial x^2}(x,t)=LC\frac{{\partial }^{2}I}{\partial t^2}(x,t)+(RC+GL)\frac{\partial I}{\partial t}(x,t)+GRI(x,t)$

Modèle en Pi

Impédance et admittance

Modèle en Pi

En considérant les pertes, l'impédance Zl et l'admittance Yq se calculent comme suit :

$Z_l=\mathrm{\Gamma }\cdot \sinh (\gamma \cdot l)$

$\frac{Y_q}{2}=\frac{1}{\mathrm{\Gamma }}\tanh (\gamma \cdot \frac{l}{2})$

Avec $\gamma =\alpha +j\mathrm{B}=\sqrt{Z^{\prime }\cdot Y^{\prime }}$ la constante de propagation, avec Z' l'impédance linéique de la ligne et Y' l'admittance linéique de la ligne. Et $\mathrm{\Gamma }=\sqrt{\frac{Z^{\prime }}{Y^{\prime }}}$, l'impédance de la ligne. l est la longueur de la ligne.

Pour une ligne sans perte :

$Z_l=\mathrm{\Gamma }\cdot j\cdot \sin (\mathrm{B}\cdot l)$

$\frac{Y_q}{2}=\frac{1}{\mathrm{\Gamma }}j\cdot \tan (\mathrm{B}\cdot \frac{l}{2})$

Pour une ligne aérienne courte, inférieure à Modèle:Unité, on peut négliger les capacitances et simplifier l'impédance :

$Z_l=Z^{\prime }\cdot l$

$\frac{Y_q}{2}=0$ ou $\frac{Y_q}{2}=\frac{Y^{\prime }\cdot l}{2}$

Nombre de Pi à utiliser

Une section en Pi n'est constituée que d'éléments concentrés. Avec une seule section, le modèle en Pi n'est valable qu'en basse fréquence pour de faible longueur de ligne. Quand la longueur ou la fréquence augmente, le nombre de sections en Pi à connecter en série pour avoir une modélisation correcte doit être augmenté.

Une ligne peut être considérée comme "courte", c'est-à-dire modélisable avec une seule section en Pi, jusqu'à Modèle:Unité pour une ligne aérienne en Modèle:Unité et de Modèle:Unité pour un cable. Le nombre de sections en Pi doit augmenter proportionnellement avec la fréquence et inversement proportionnel à la longueur de ligneModèle:,.

Calcul des paramètres électriques pour une ligne aérienne

Conducteur équivalent

Faisceaux de conducteur de 2, 3 ou 4 conducteurs

Les lignes à haute tension, surtout à plus de Modèle:Unité, ne possèdent pas un conducteur unique par phase, mais de faisceaux de conducteurs en contenant de 2 à 4 (voir image ci-contre). Il est possible de modéliser un faisceau de conducteurs par un conducteur équivalent de rayon :

$r_{\text{equivalent}}=\sqrt[n]{n\cdot r_C\cdot r_T^{n-1}}$

Où r_equivalent est le rayon équivalent du faisceau, r_C le rayon des conducteurs, r_T le rayon du cercle formé par le faisceau, n le nombre de conducteurs par faisceau (voir image).

Distance inter-faisceaux / conducteur équivalente

Distance entre les faisceaux de conducteur sur un pylône

Pour un système triphasé, il est possible de définir une distance équivalente entre les conducteurs, ou faisceaux de conducteurs selon le cas, en calculant la moyenne géométrique. Dans le cas d'un système triphasé simple, elle vaut :

$D=\sqrt[3]{D_{12}\cdot D_{23}\cdot D_{31}}$

Pour le cas d'un système double (deux lignes triphasés de chaque côté du pylône) :

$D=\sqrt[3]{D_{12}\cdot D_{23}\cdot D_{31}\cdot \frac{D_{12^{\prime }}\cdot D_{23^{\prime }}\cdot D_{31^{\prime }}}{D_{11^{\prime }}\cdot D_{22^{\prime }}\cdot D_{33^{\prime }}}}$

Résistance de la ligne

La résistance linéaire d'un conducteur à Modèle:Unité est :

$R_{20}=\frac{\rho }{S}$

Avec $S$ la section et $\rho$ la résistivité du matériau conducteur. Pour un conducteur en cuivre la résistivité est de l'ordre de 1,8 x 10Modèle:Exp Ω∙m pour de l'aluminium de 3 x 10Modèle:Exp Ω∙m.

La résistance de la ligne dépend également de la température :

$R=R_{20}\cdot (1+\alpha \mathrm{\Delta }T)$

Où $\alpha$ est la coefficient de température et $\mathrm{\Delta }T$ la différence en kelvins entre la température et Modèle:Unité.

Dans le cas d'un faisceaux de conducteurs, ces derniers étant en parallèle la résistance doit être divisée par le nombre de conducteurs.

Inductance

L'inductance linéique d'une ligne vaut :

${L_{\text{ligne}}}^{\prime }=\frac{{\mu }_0}{2\pi }(\ln \left(\frac{D}{r}\right)+\frac{{\mu }_r}{4n})$

Avec n le nombre de conducteurs par faisceau et ${\mu }_r$ la permittivité du conducteur. Dans le cas ${\mu }_r$ est égal à 1, on peut définir un rayon équivalent $r_{GMR}=r\cdot e^{-1/4n}$:

${L_{\text{ligne}}}^{\prime }=\frac{{\mu }_0}{2\pi }\ln \left(\frac{D}{r_{GMR}}\right)$

Valeurs typiques de l'impédance

Ci-dessous quelques valeurs typique pour un réseau Modèle:Unité avec des conducteurs aluminium / acier de section d'aluminium Modèle:Unité et d'acier Modèle:UnitéModèle:,.

Tension de la ligne (kV)	Nombre de conducteurs par faisceau	Impédance (Ω/km)
110	1	0,12 + j0,4
220	2	0,06 + j0,3
380	4	0,03 + j0,25

D'autres valeurs pour la résistance seulement :

Tension de la ligne (kV)	Nombre de conducteurs par faisceau	Résistance (Ω/km)
70	1	0,09-0,35
110	1	0,12
220	2	0,04-0,09
380	4	0,03

Et l'inductance :

Tension de la ligne (kV)	Nombre de conducteurs par faisceau	Inductance (Ω/km)
70	1	0,2 - 0,4
110	1	0,4
220	2	0,3
380	4	0,25

Capacité

Capacités présentes dans un système triphasé

Dans un système triphasé, il y a des capacités entre les lignes et la terre, mais également entre lignes. L'objectif est de synthétiser le tout dans une seule capacité "moyenne" C_b égale pour les trois lignes :

${C_b}^{\prime }=\frac{2\pi {ϵ}_0{ϵ}_r}{\ln \left(\frac{D}{r}\right)}$

Dans laquelle les ${ϵ}_0$ et ${ϵ}_r$ sont les permittivité diélectrique du vide et du matériau (dans le cas de l'air pour les lignes ${ϵ}_r$ vaut environ 1).

On peut démontrer en utilisant le théorème de Kennelly que :

${C_b}^{\prime }=3\cdot C_L+C_T$

Avec C_L la capacité mutuelle et C_T la capacité à la terre

Conductance

Une résistance doit être représentée en parallèle aux capacités pour être complet. Elle est due au effet corona et aux fuites de courant (causées par la pollution sur les isolateurs par exemple). Pour une ligne de Modèle:Unité elle vaut :

Temps sec	Temps humide
3 nS/km	30 nS/km

Valeurs typiques de l'admittance

Ci-dessous quelques valeurs typiques pour un réseau Modèle:Unité.

Tension de la ligne (kV)	Nombre de conducteurs par faisceau	Admittance (uS/km)
110	1	3
220	2	3,9
380	4	4,3

Calcul des paramètres électriques pour un câble

Admittance

Différents rayons d'un câble électrique avec un seul écran.

Pour les câbles, les calculs de résistance et d'inductivité sont identiques. La capacité vaut :

$C_T={C_b}^{\prime }=\frac{2\pi ϵ}{\ln (\frac{r_2}{r_1})}$

Avec r₁ le rayon de l'âme et r₂ le rayon intérieur de l'écran. La capacité entre les lignes est négligeable.

La conductance est égale à:

${G_b}^{\prime }=\tan (\delta )\cdot \omega {C_b}^{\prime }$

Quelques valeurs typiquesModèle:,Modèle:, :

Tension de la ligne (kV)	Résistance (Ω/km)	Réactance (Ω/km)	Admittance ((uS/km)
36	0,06-0,16	0,10 - 0,17	40 -120
150	0,03-0,12	0,12 - 0,22	30 - 70

Type d'isolation du câble	$tan(\delta )$	${ϵ}_r$
Papier imprégné	2 - 3 10Modèle:-3	3,3-3,5
PVC		3,5 - 8,0
Éthylène propylène		2,8 - 3,5
Polyéthylène	0,2 - 0,5 10Modèle:-3	2,2-2,3
Polyéthylène réticulé		2,3 - 6

La norme IEC 60287-1-1 fournit de nombreuses formules pour le calcul des paramètres électriques des câbles.

Transposition des lignes

Différents motifs de transposition des lignes

Exemple de pylône de transposition

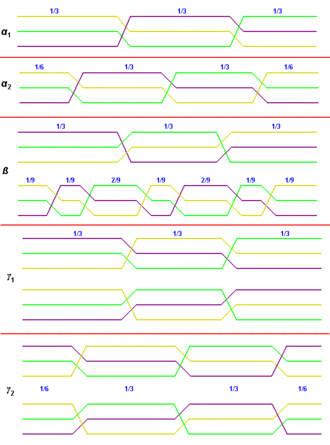
La capacité ligne-terre dépend de la hauteur à laquelle se trouve le conducteur ou faisceau de conducteur. Dans les exemples précédents, un de ces conducteurs se trouve plus haut que les deux autres. Si rien n'est fait, la capacité de cette phase vis-à-vis de la terre serait différente de celle des deux autres phases, ce qui n'est pas souhaitable pour un système triphasé symétriqueModèle:,.

Pour résoudre le problème, on commute les phases entre elles à intervalle régulier au moyen d'un pylône de transposition. Pour des lignes d'une longueur inférieure à Modèle:Unité deux transpositions, ce qui permet à chaque ligne d'avoir en moyenne le même comportement capacitif, suffisent. Les courants induits par les trois phases se compensent alors.

Voir aussi

• angle de transport

Bibliographie

• Modèle:Ouvrage

Normes

• IEC 60287-1-1 Câbles électriques – Calcul du courant admissible – Partie 1-1: Equations de l’intensité du courant admissible (facteur de charge 100 %) et calcul des pertes – Généralités, 2006
• CIGRÉ Brochure 531 Cable Systems Electrical Characteristics, 2013

Lien externe

• Modèle:Lien web