Objet exponentiel

En mathématiques, et plus particulièrement en théorie des catégories, un objet exponentiel est un équivalent catégorique à un espace fonctionnel en théorie des ensembles. Les catégories avec tous les produits finis et tous les objets exponentiels sont appelées catégories cartésiennes fermées. Un objet exponentiel peut aussi être appelé un objet puissance ou objet des morphismes.

Définition

Soit C une catégorie avec produits et soient Y et Z des objets de C. L'objet exponentiel Z^Y peut être défini comme un morphisme universel du foncteur –×Y à Z. (Le foncteur –×Y de C dans C envoie l'objet X sur X×Y et le morphisme φ sur φ×id_Y).

Explicitement, un objet Z^Y avec un morphisme $\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}:(Z^Y\times Y)\to Z$ est un objet exponentiel si pour tout objet X et tout morphisme g : (X×Y) → Z il existe un unique morphisme $\lambda g:X\to Z^Y$ tel que le diagramme suivant commute :

Universal property of the exponential object

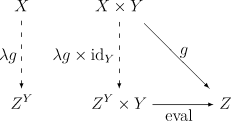
Si l'objet exponentiel Z^Y existe pour tous les objets Z dans C, alors le foncteur qui envoie Z sur Z^Y est un adjoint à droite du foncteur –×Y. Dans ce cas, il y a une bijection naturelle entre les ensembles des morphismes

$\mathrm{H}\mathrm{o}\mathrm{m}(X\times Y,Z)\cong \mathrm{H}\mathrm{o}\mathrm{m}(X,Z^Y).$

Les morphismes $g$ et $\lambda g$ sont parfois appelés adjoints exponentiels.

On remarque que pour $A,B$ dans la catégorie des ensembles, $A^B=\mathrm{H}\mathrm{o}\mathrm{m}(B,A)$.

Exemples

• Dans la catégorie des ensembles, l'objet exponentiel $Z^Y$ est l'ensemble de toutes les applications de $Y$ dans $Z$. L'application $\mathrm{e}\mathrm{v}\mathrm{a}\mathrm{l}:(Z^Y\times Y)\to Z$ est l'application évaluation qui envoie la paire (f, y) sur f(y). Pour toute application $g:(X\times Y)\to Z$, l'application $\lambda g:X\to Z^Y$ est la forme curryfiée de g :

$\lambda g(x)(y)=g(x,y).$

• Dans la catégorie des espaces topologiques, l'objet exponentiel Z^Y existe si Y est un espace localement compact. Dans ce cas, l'espace Z^Y est l'ensemble de toutes les applications continues de Y dans Z muni de la topologie compacte-ouverte. L'application évaluation est la même que pour la catégorie des ensembles. Si Y n'est pas localement compact, l'objet exponentiel peut ne pas exister (l'espace Z^Y existe toujours mais n'est pas forcément un objet exponentiel car l'évaluation peut ne pas être continue). Pour cette raison, la catégorie des espaces topologique n'est pas cartésienne fermée.

Références

• Modèle:OuvrageModèle:Références

Liens externes

• Page web interactive écrite par Jocelyn Paine qui génère des exemples d'objets exponentiels et d'autres constructions catégoriques.