Pendule double

En mécanique, on désigne par pendule double un pendule à l'extrémité duquel on accroche un autre pendule. Son évolution est généralement chaotique.

Mise en équations

Un pendule double est un système dynamique typiquement limité à un mouvement plan. Il comporte deux degrés de libertés ( $θ_{1}, θ_{2}$ ) et cinq paramètres ( $l_{1}, l_{2}, m_{1}, m_{2}, g$ ).

Approche lagrangienne

Le pendule est constitué de deux tiges de longueur $l_{1}$ et $l_{2}$ , de masse nulle et deux masses $m_{1}$ et $m_{2}$ .

L'énergie cinétique vaut :
$T = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2} = \frac{1}{2} m_{1} l_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} [l_{1}^{2} {\dot{θ}}_{1}^{2} + l_{2}^{2} {\dot{θ}}_{2}^{2} + 2 l_{1} l_{2} {\dot{θ}}_{1} {\dot{θ}}_{2} \cos (θ_{1} - θ_{2})]$
où $θ_{i}$ est l'angle par rapport à la verticale et $v_{i}$ la vitesse du pendule $i$ .
L'énergie potentielle vaut :
$V = m_{1} g z_{1} + m_{2} g z_{2}$ ( $z_{i}$ étant l'altitude de la masse $i$ ), ou
$V = - (m_{1} + m_{2}) g l_{1} \cos (θ_{1}) - m_{2} g l_{2} \cos (θ_{2})$ .
Le lagrangien vaut donc :
$L = T - V$ , soit
$L = \frac{1}{2} (m_{1} + m_{2}) l_{1}^{2} {\dot{θ}}_{1}^{2} + \frac{1}{2} m_{2} l_{2}^{2} {\dot{θ}}_{2}^{2} + m_{2} l_{1} l_{2} {\dot{θ}}_{1} {\dot{θ}}_{2} \cos (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g l_{1} \cos (θ_{1}) + m_{2} g l_{2} \cos (θ_{2})$

En appliquant les équations de Lagrange, on obtient les équations du mouvement :

$\begin{matrix} (m_{1} + m_{2}) l_{1} {\ddot{θ}}_{1} + m_{2} l_{2} {\ddot{θ}}_{2} \cos (θ_{1} - θ_{2}) + m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g \sin (θ_{1}) = 0 \\ l_{1} {\ddot{θ}}_{1} \cos (θ_{1} - θ_{2}) + l_{2} {\ddot{θ}}_{2} - l_{1} {\dot{θ}}_{1}^{2} \sin (θ_{1} - θ_{2}) + g \sin (θ_{2}) = 0 \end{matrix}$

Dans le cas particulier $m_{1} = m_{2}, l_{1} = l_{2}$ , dans un système d'unités idoine, en renommant $θ_{1}, θ_{2}$ en $ϕ, ψ$ , et en ajoutant trois variables intermédiaires, ces équations deviennent :

Modèle:Bloc emphase

Aucune solution explicite n'étant connue, la résolution passe typiquement par l'utilisation de méthodes numériques.

Autour du minimum énergétique (voir section suivante), ce système possède des solutions périodiques décomposables en deux modes, mais il est chaotique, c’est-à-dire qu'il possède aussi des solutions ni périodiques ni pseudo-périodiques, mais présentant en permanence un mouvement original, et qu'il est alors sensible aux conditions initiales.

Approximation des petites oscillations

Le système est à l'équilibre pour $θ_{1} = θ_{2} = {\dot{θ}}_{1} = {\dot{θ}}_{2} = 0$ . Pour de petites oscillations autour de ces valeurs, nous pouvons introduire les approximations de MacLaurin $\sin θ = θ$ et $\cos θ = 1$ . Les équations du mouvement peuvent alors être réduites au système linéaire:

\begin{matrix} (m_{1} + m_{2}) l_{1} {\ddot{θ}}_{1} & + & m_{2} l_{2} {\ddot{θ}}_{2} & + & (m_{1} + m_{2}) g θ_{1} & = & 0 \\ l_{1} {\ddot{θ}}_{1} & + & l_{2} {\ddot{θ}}_{2} & + & g θ_{2} & = & 0 \end{matrix}

Le double pendule peut alors être analysé en termes de modes normaux, en remarquant que le système ci-dessus peut être réduit à la forme matricielle $M \ddot{\vec{θ}} + K \vec{θ} = \vec{0}$ .

Par exemple, pour $m_{1} = m_{2}$ et $l_{1} = l_{2} = l$ , ce système s'écrit : Modèle:Retrait

Approche Newtonienne

Les équations du mouvement peuvent également être trouvées en utilisant les complexes.

Représentons le double pendule ci-dessus dans le plan complexe de Gauss, en posant que l’axe des réels a même sens et même direction que la gravitation. Les points m₁ et m₂ représentant les mobiles 1 et 2 correspondent aux affixes z₁ et z₂. En fait, seuls les angles vont varier en fonction du temps puisque la masse et la longueur sont des constantes. Il faut donc chercher une manière de représenter les fonctions $θ_{1}$ et $θ_{2}$ .

Dès lors, puisque le module de z₁ vaut l₁, son argument $θ_{1}$ , $z_{1} = l_{1} (\cos θ_{1} + i \sin θ_{1}) = l_{1} e^{i θ_{1}}$ . Ensuite, observons que z₂ est issu d’une translation de z₁ par le complexe z₀= $l_{2} e^{i θ_{2}}$ , c’est-à-dire un complexe tel que son module vaut l₂ et son argument $θ_{2}$ . En d’autres termes, z₂ = z₁ + z₀, donc $z_{2} = l_{1} e^{i θ_{1}} + l_{2} e^{i θ_{2}}$

Ici, les complexes z₁ et z₂ déterminent la position des mobiles1 et 2 en fonction du temps puisque $θ_{1} (t)$ et $θ_{2} (t)$ sont des fonctions du temps. L'accélération d'une masse mobile s'obtient en dérivant deux fois par rapport au temps la fonction définissant sa position. Ainsi, l’accélération de z₁ vaut

$a_{z_{1}} = \frac{d^{2} z_{1}}{d t^{2}} = l_{1} (i {\ddot{θ}}_{1} - {\dot{θ}}_{1}^{2}) e^{i θ_{1}}$

et que celle de la deuxième est égale à

$a_{z_{2}} = \frac{d^{2} z_{2}}{d t^{2}} = l_{1} (i {\ddot{θ}}_{1} - {\dot{θ}}_{1}^{2}) e^{i θ_{1}} + l_{2} (i {\ddot{θ}}_{2} - {\dot{θ}}_{2}^{2}) e^{i θ_{2}}$

Notons-les respectivement ${\ddot{z}}_{1}$ et ${\ddot{z}}_{2}$ .

Revenons dans la vie réelle. Quand une masse est suspendue à une corde, une tension se produit le long de celle-ci. Appelons, T₁ et T₂, les tensions exercées par les masses m₁ et m₂ et représentons-les sous forme de complexes t₁ et t₂.

Nous observons alors que t₁, z₁ et 0 sont alignés ou colinéaires, ce qui permet d’écrire que $t_{1} = k_{1} z_{1} (k_{1} \in ℝ)$ . De même, t₂, z₀ et 0 sont alignés, ce qui permet d’affirmer que $t_{2} = k_{2} z_{0} (k_{2} \in ℝ)$ .

La formule de la dynamique F = m a, connue aussi sous le nom de la Modèle:2e loi de Newton, dit que la somme de toutes les forces appliquées à un mobile est égale au produit de l’accélération de celui-ci par sa masse.

Le mobile 2 est soumis à la tension T₂ et la force due à la gravité m₂ g, donnant les relations suivantes :

$F = m a_{z_{2}} = t_{2} + m_{2} g ⟺ m_{2} {\ddot{z}}_{2} - m_{2} g = t_{2} ⟺ {\ddot{z}}_{2} - g = \frac{t_{2}}{m_{2}} = \frac{k_{2} z_{0}}{m_{2}} \Rightarrow \frac{{\ddot{z}}_{2} - g}{z_{0}} = \frac{k_{2}}{m_{2}} . . . (1)$

Le mobile 1 est soumis à la tension T₁, à la force due à la gravité m₁g et à la tension T₂’ qui est issue du principe des actions réciproques (la Modèle:3e loi de Newton) telle que T₂’= - T₂. Dès lors, nous pouvons dire que

$F = m a_{z_{1}} = t_{1} - t_{2} + m_{1} g ⟺ t_{1} = t_{2} - m_{1} g + m_{1} {\ddot{z}}_{1} ⟺ t_{1} = m_{2} {\ddot{z}}_{2} - m_{2} g - m_{1} g + m_{1} {\ddot{z}}_{1}$

$⟺ m_{2} {\ddot{z}}_{2} - m_{2} g - m_{1} g + m_{1} {\ddot{z}}_{1} = k_{1} z_{1} ⟺ \frac{m_{2} {\ddot{z}}_{2} - m_{2} g - m_{1} g + m_{1} {\ddot{z}}_{1}}{z_{1}} = k_{1} . . . (2)$

Les membres de droite des équations (1) et (2) étant réels, exprimons que la partie imaginaire des membres de gauche est nulle :

Tout d’abord, concernant l’équation (1).

Calculons le membre de gauche.

$\frac{{\ddot{z}}_{2} - g}{z_{0}} = \frac{l_{1} (i {\ddot{θ}}_{1} - {\dot{θ}}_{1}^{2}) e^{i θ_{1}} + l_{2} (i {\ddot{θ}}_{2} - {\dot{θ}}_{2}^{2}) e^{i θ_{2}} - g}{l_{2} e^{i θ_{2}}}$

$= \frac{l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1} + l_{2} i {\ddot{θ}}_{2} \cos θ_{2} - l_{2} {\dot{θ}}_{2}^{2} \cos θ_{2} - l_{2} {\ddot{θ}}_{2} \sin θ_{2} - l_{2} i {\dot{θ}}_{2}^{2} \sin θ_{2} - g}{l_{2} \cos θ_{2} + l_{2} i \sin θ_{2}}$

Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par $\frac{\cos θ_{2} - i \sin θ_{2}}{\cos θ_{2} - i \sin θ_{2}}$ .

Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous conservons alors uniquement :

$(l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1} + l_{2} i {\ddot{θ}}_{2} \cos θ_{2} - l_{2} i {\dot{θ}}_{2}^{2} \sin θ_{2}) (\cos θ_{2})$

$+ (- l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1} - l_{2} {\dot{θ}}_{2}^{2} \cos θ_{2} - l_{2} {\ddot{θ}}_{2} \sin θ_{2} - g) (- i \sin θ_{2})$

Ainsi, nous pouvons affirmer que :

$Im (\frac{{\ddot{z}}_{2} - g}{z_{0}})$

$= \frac{l_{1} {\ddot{θ}}_{1} \cos θ_{1} \cos θ_{2} - l_{1} {\dot{θ}}_{1}^{2} \sin θ_{1} \cos θ_{2} + l_{2} {\ddot{θ}}_{2} \cos^{2} θ_{2} - l_{2} {\dot{θ}}_{2}^{2} \cos θ_{2} \sin θ_{2}}{l_{2}}$

$+ \frac{l_{1} {\dot{θ}}_{1}^{2} \sin θ_{2} \cos θ_{1} + l_{1} {\ddot{θ}}_{1} \sin θ_{1} \sin θ_{2} + l_{2} {\dot{θ}}_{2}^{2} \sin θ_{2} \cos θ_{2} + l_{2} {\ddot{θ}}_{2} \sin^{2} θ_{2} + g \sin θ_{2}}{l_{2}}$

$= \frac{l_{1} {\ddot{θ}}_{1} \cos (θ_{1} - θ_{2}) + l_{2} {\ddot{θ}}_{2} - l_{1} {\dot{θ}}_{1}^{2} \sin (θ_{1} - θ_{2}) + g \sin (θ_{2})}{l_{2}}$

Comme il faut que la partie imaginaire soit nulle, nous obtenons cette première équation différentielle.

$l_{1} {\ddot{θ}}_{1} \cos (θ_{1} - θ_{2}) + l_{2} {\ddot{θ}}_{2} - l_{1} {\dot{θ}}_{1}^{2} \sin (θ_{1} - θ_{2}) + g \sin (θ_{2}) = 0$

Ensuite, concernant l’équation (2). Nous procédons de la même manière. Calculons le membre de gauche.

$\frac{m_{2} {\ddot{z}}_{2} - m_{2} g - m_{1} g + m_{1} {\ddot{z}}_{1}}{z_{1}}$

$= \frac{m_{2} [l_{1} (i {\ddot{θ}}_{1} - {\dot{θ}}_{1}^{2}) (\cos θ_{1} + i \sin θ_{1}) + l_{2} (i {\ddot{θ}}_{2} - {\dot{θ}}_{2}^{2}) (\cos θ_{2} + i \sin θ_{2})] - m_{2} g - m_{1} g + m_{1} [l_{1} (i {\ddot{θ}}_{1} - {\dot{θ}}_{1}^{2}) (\cos θ_{1} + i \sin θ_{1})]}{l_{1} \cos θ_{1} + l_{1} i \sin θ_{1}}$

$= \frac{m_{1} [l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1}] - m_{1} g - m_{2} g}{l_{1} \cos θ_{1} + l_{1} i \sin θ_{1}}$

$+ \frac{m_{2} [l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1} + l_{2} i {\ddot{θ}}_{2} \cos θ_{2} - l_{2} {\dot{θ}}_{2}^{2} \cos θ_{2} - l_{2} {\ddot{θ}}_{2} \sin θ_{2} - l_{2} i {\dot{θ}}_{2}^{2} \sin θ_{2}]}{l_{1} \cos θ_{1} + l_{1} i \sin θ_{1}}$

Appliquons le binôme conjugué pour supprimer le terme imaginaire au dénominateur, ce qui revient à multiplier la fraction par $\frac{\cos θ_{1} - i \sin θ_{1}}{\cos θ_{1} - i \sin θ_{1}}$ .

Maintenant, seuls les imaginaires purs intéressent. C’est pourquoi, relevons uniquement les imaginaires purs issus du produit du numérateur par le conjugué du dénominateur. Nous gardons alors uniquement

$[m_{1} (l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1}) + m_{2} (l_{1} i {\ddot{θ}}_{1} \cos θ_{1} - l_{1} i {\dot{θ}}_{1}^{2} \sin θ_{1} + l_{2} i {\ddot{θ}}_{2} \cos θ_{2} - l_{2} i {\dot{θ}}_{2}^{2} \sin θ_{2})] [\cos θ_{1}]$

$+ [m_{1} (- l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1}) + m_{2} (- l_{1} {\dot{θ}}_{1}^{2} \cos θ_{1} - l_{1} {\ddot{θ}}_{1} \sin θ_{1} - l_{2} {\dot{θ}}_{2}^{2} \cos θ_{2} - l_{2} {\ddot{θ}}_{2} \sin θ_{2}) - m_{1} g - m_{2} g] [- i \sin θ_{1}]$

Ainsi, nous pouvons affirmer que

$Im (\frac{m_{2} {\ddot{z}}_{2} - m_{2} g - m_{1} g + m_{1} {\ddot{z}}_{1}}{z_{1}})$

$= \frac{m_{1} l_{1} {\ddot{θ}}_{1} \cos^{2} θ_{1} - m_{1} l_{1} {\dot{θ}}_{1}^{2} \sin θ_{1} \cos θ_{1} + m_{2} l_{1} {\ddot{θ}}_{1} \cos^{2} θ_{1} - m_{2} l_{1} {\dot{θ}}_{1}^{2} \sin θ_{1} \cos θ_{1} + m_{2} l_{2} {\ddot{θ}}_{2} \cos θ_{1} \cos θ_{2}}{l_{1}}$

$+ \frac{- m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin θ_{2} \cos θ_{1} + m_{1} l_{1} {\dot{θ}}_{1}^{2} \sin θ_{1} \cos θ_{1} + m_{1} l_{1} {\ddot{θ}}_{1} \sin^{2} θ_{1} + m_{2} l_{1} {\dot{θ}}_{1}^{2} \sin θ_{1} \cos θ_{1} + m_{2} l_{1} {\ddot{θ}}_{1} \sin^{2} θ_{1}}{l_{1}}$

$+ \frac{m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin θ_{1} \cos θ_{2} + m_{2} l_{2} {\ddot{θ}}_{2} \sin θ_{1} \sin θ_{2} + m_{1} \sin θ_{1} g + m_{2} \sin θ_{1} g}{l_{1}}$

$= \frac{(m_{1} + m_{2}) l_{1} {\ddot{θ}}_{1} + m_{2} l_{2} {\ddot{θ}}_{2} \cos (θ_{1} - θ_{2}) + m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g \sin (θ_{1})}{l_{1}}$

Comme il faut que la partie imaginaire soit nulle, nous obtenons cette deuxième différentielle.

$(m_{1} + m_{2}) l_{1} {\ddot{θ}}_{1} + m_{2} l_{2} {\ddot{θ}}_{2} \cos (θ_{1} - θ_{2}) + m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g \sin (θ_{1}) = 0$

Nous avons donc pour finir :

${\begin{matrix} l_{1} {\ddot{θ}}_{1} \cos (θ_{1} - θ_{2}) + l_{2} {\ddot{θ}}_{2} - l_{1} {\dot{θ}}_{1}^{2} \sin (θ_{1} - θ_{2}) + g \sin (θ_{2}) = 0 \\ (m_{1} + m_{2}) l_{1} {\ddot{θ}}_{1} + m_{2} l_{2} {\ddot{θ}}_{2} \cos (θ_{1} - θ_{2}) + m_{2} l_{2} {\dot{θ}}_{2}^{2} \sin (θ_{1} - θ_{2}) + (m_{1} + m_{2}) g \sin (θ_{1}) = 0 \end{matrix}$

Ce sont les mêmes équations que pour l'approche lagrangienne.

Pendule à entraînement circulaire uniforme

Un autre exercice classique concerne le cas où la première tige se meut d'un mouvement uniforme autour de son axe. On a alors $\dot{θ_{1}} = ω$ et l'équation différentielle du mouvement, issue de (2), s'écrit, en posant $θ_{2} = θ$ :

$l_{2} \ddot{θ} = - l_{1} ω^{2} \sin (θ - ω t) - g \sin θ = - (1 + \frac{l_{1} ω^{2}}{g} \cos ω t) g \sin θ + l_{1} ω^{2} \sin ω t \cos θ$ .

Pour de petites oscillations et $\frac{l_{1} ω^{2}}{g} < < 1$ , l'équation se linéarise en $l_{2} \ddot{θ} + g θ = l_{1} ω^{2} \sin (ω t)$ et le système se comporte donc en oscillateur harmonique forcé :

Mais si, dans ce cas, on choisit $ω = \sqrt{g / l_{2}}$ , on obtient un phénomène de résonance ; par définition, les petites oscillations ne restent pas petites, et l'on tombe en fait dans un mouvement chaotique :

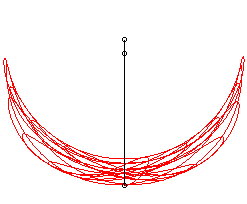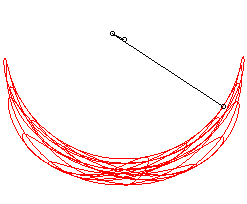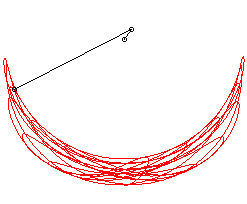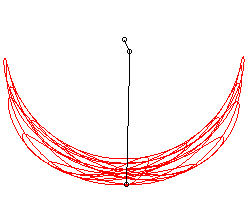On constate que le pendule fait le tour si $l_{2} / l_{1} < 4, 3$

Notes et références

Modèle:Références

Voir aussi

Pendule simple

Liens externes

Modèle:Portail

Pendule double

Sommaire

Mise en équations

Approche lagrangienne

Approximation des petites oscillations

Approche Newtonienne

Pendule à entraînement circulaire uniforme

Notes et références

Voir aussi

Liens externes

Menu de navigation

Pendule double

Mise en équations

Approche lagrangienne

Approximation des petites oscillations

Approche Newtonienne

Pendule à entraînement circulaire uniforme

Notes et références

Voir aussi

Liens externes

Menu de navigation

Rechercher