Pyramide

Modèle:Voir homonymes1

Ensemble des pyramides

Faces	$n$ triangles, 1 n-gone
Arêtes	2 $n$
Sommets	$n$ + 1
Groupe des isométries	_D2n
Polyèdre dual	Auto-duales
Propriétés	convexe

En géométrie, une pyramide (du grec ancien Modèle:Grec ancien) à $n$ côtés est un polyèdre à $n$ + 1 faces, formé en reliant une base polygonale à $n$ côtés à son sommet, ou sommet opposé à la base (également appelé apex), par $n$ faces triangulaires ( $n ⩾ 3$ ).

Lorsque cela n'est pas précisé, la base est supposée carrée. Pour une pyramide triangulaire chaque face peut servir de base, avec le sommet opposé pour apex. Le tétraèdre régulier, un des solides de Platon, est une pyramide triangulaire. Les pyramides carrées ainsi que les pentagonales peuvent aussi être construites avec toutes les faces régulières, et par conséquent être des solides de Johnson. Toutes les pyramides sont auto-duales.

Les pyramides forment une sous-classe des prismatoïdes.

Origine du nom

Le mot « pyramide » vient du grec ancien Modèle:Grec ancien transmis au latin sous la forme Modèle:Langue^[1] mais son origine est incertaine. Certains la rattachent à la notion de feu (racine grecque pyr)^[2] et citent Platon qui voyait dans le tétraèdre régulier (en forme de pyramide) le symbole du feu^[3]. D'autres y voient un mot dérivé du grec « puros » signifiant « froment » rappelant que c'était la forme des greniers royaux^[2]. D'autres y voient encore une déformation de l'égyptien, soit du mot « haram (ou rem) » qui s'écrit h-r-m en égyptien^[2] et qui est leur nom en égyptien, soit du mot « pr-m-ous » qui désigne en égyptien une ligne déterminante de la pyramide^[4]. D'autres enfin signalent que ce mot « pyramis » désignait en grec un gâteau de miel et de farine^[4].

Volume

Le volume d'un cône et en particulier d'une pyramide est

V = \frac{1}{3} S h

où

S

est l'aire de la base et

h

la hauteur de la base à son sommet, c'est-à-dire la plus petite distance entre la base et son sommet.

En particulier, le volume d'une pyramide à base carrée avec une hauteur égale à la moitié de la base peut être vue comme un sixième d'un cube formé par six pyramides de cette sorte (en paires opposées) par le centre. Alors « base fois hauteur » correspond à un demi du volume du cube, et par conséquent trois fois le volume de la pyramide, ce qui donne bien le facteur un tiers.

Le volume d'une pyramide à base carrée et composée de triangles équilatéraux est le double de celui d'un tétraèdre de même côté, ce qui se démontre par dissection moitié.

Aire de la surface

L'aire de la surface d'une pyramide régulière, c'est-à-dire une pyramide dont toutes les faces sont des triangles isocèles identiques, est

S = S_{b} + \frac{p l}{2}

où Modèle:Math est l'aire de la base,

p

le périmètre de la base et

l

la longueur de la bissectrice d'une face (i.e. la longueur à partir du milieu d'une arête quelconque de la base jusqu'à l'apex).

Pyramides avec des faces polygonales

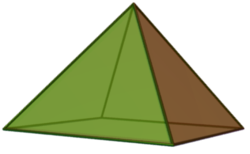
Si toutes les faces sont des polygones réguliers, la base de la pyramide peut être un polygone régulier de 3, 4 ou 5 côtés :

Nom	Tétraèdre	Pyramide carrée	Pyramide pentagonale

Classe	Solide de Platon	Solide de Johnson (J1)	Solide de Johnson (J2)
Base	Triangle équilatéral	Carré	Pentagone régulier
Groupe de symétrie	T_d	C_4v	C_5v

Le centre géométrique d'une pyramide carrée est localisé sur l'axe de symétrie, à un quart de son hauteur.

Symétrie

Si la base est régulière et son sommet est au-dessus du centre, le groupe des isométries d'une pyramide à $n$ côtés est le groupe diédral $D_{2 n}$ , d'ordre $2 n$ , excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de symétrie plus grand T_d d'ordre 24, lequel a quatre versions de $D_{6}$ pour sous-groupes.

Le groupe de rotation est $C_{n}$ , d'ordre $n$ , excepté dans le cas d'un tétraèdre régulier, qui possède le groupe de rotation plus grand T d'ordre 12, qui a quatre versions de $C_{3}$ pour sous-groupes.

Généralisation aux dimensions supérieures

Une pyramide est un objet géométrique ayant pour base un polygone quelconque, auquel on relie tous ses sommets à un point unique. Par abus de langage, on dit qu'elle est régulière si toutes ses faces sont des polygones réguliers.

En généralisant, une hyperpyramide de dimension 4 est un polychore ayant pour base un polyèdre auquel on relie tous ses sommets à un point unique. Le pentachore en est l'exemple le plus simple.

Et donc, une hyperpyramide de dimension $n$ est un polytope à $n$ dimensions, qui a pour base un polytope à $n - 1$ dimensions, et dont tous les sommets sont reliés à un point unique. Une hyperpyramide peut être considérée comme l'ensemble de tous les « états » pris par sa base lors de son rétrécissement progressif jusqu'à l'apex le long d'une médiane centrale (reliant le centre de gravité de la base au sommet) ; tous ces « états » de la base sont en fait l'intersection de l'hyperpyramide avec des hyperplans parallèles à la base.
L'hypervolume d'une hyperpyramide de dimension $n$ est donné par la formule :

V_{n} = \frac{B_{n - 1} \times h}{n},

où Modèle:Math est l'hypervolume de la base et $h$ la hauteur.

**Les premières hyperpyramides**
Nom	Point	Segment	Triangle	Pyramide	4-hyperpyramide	5-hyperpyramide
Explication	rien (d=-1) n'est relié à un point (d=0)	un point (d=0) est relié à un point (d=0)	un segment (d=1) est relié à un point (d=0)	un polygone (d=2) est relié à un point (d=0)	un polyèdre (d=3) est relié à un point (d=0)	un polychore (d=4) est relié à un point (d=0)
Dimension	0	1	2	3	4	5
Image