Stabilité longitudinale d'un avion

La stabilité longitudinale d'un avion est son aptitude à revenir de lui-même à une position d'équilibre en tangage quand son incidence a été modifiée par le pilote ou par un agent extérieur (ascendance, turbulence).

Cet article se présente en quatre parties :

Éléments de la stabilité longitudinale. L'étude de la stabilité passe au préalable par l'étude de l'équilibre. Cette étude de l'équilibre nécessite elle-même une description précise des forces aérodynamiques sur un profil.

Équilibre des moments précise la condition d'équilibre et le rôle essentiel de l'empennage.

Stabilité longitudinale aborde la stabilité statique qui implique la position du centre de masse de l'avion.

Stabilité dynamique présente la compréhension du retour à l'équilibre. Cet équilibre est atteint après un mouvement oscillatoire qui est une superposition d'une oscillation de tangage de courte période et d'une oscillation de trajectoire dite phugoïde.

Élément de la stabilité longitudinale

Une machine volante à voilure fixe (avion, planeur) comporte généralement un fuselage et des surfaces portantes déstabilisantes en tangage, nécessitant l'ajout d'une surface stabilisante placée à l'arrière, appelée stabilisateur horizontal. Le stabilisateur horizontal fait partie de l'empennage de l'avion.

L'aile, surface portante et déstabilisante

L'aile surface portante, est caractérisé par un profil porteur cambré (non symétrique) qui est généralement instable en tangage (moment piqueur).

Le moment piqueur d'un profil porteur

Fig. 1 : Distribution de la pression sur un profil asymétrique à incidence de portance zéro (~-3°)

Le centre de pression d’un profil est le point de sa corde autour duquel le moment résultant des efforts aérodynamiques appliqués au profil est nul. En ce point s'applique la résultante de la portance et des forces de trainée.

En plus de la portance et de la traînée, l'effet de la distribution asymétrique des pressions sur la surface de l'aile, combiné à l'effet des contraintes de cisaillement, engendrent un moment de rotation à piquer.

Ce moment piqueur est produit par la contre-réaction au tourbillon central de Prandtl (tourbillon tournant de bas en haut, autour du bord d'attaque). Selon la théorie de la ligne portante de Prandtl, le tourbillon central est prolongé vers l'infini aval par deux tourbillons rectilignes, formant la turbulence de sillage. Bien que masqué par l'écoulement général, le tourbillon de Prandtl existe réellement sur toute l'envergure des ailes. Ce tourbillon influe sur la distribution des pressions, en déplaçant le premier point d'arrêt vers l'intrados.

La distribution des pressions sur un profil non symétrique n'est pas la même à l'extrados et à l'intrados.

La Fig. 1 montre la distribution des pressions sur la surface de l'intrados du profil d'une aile asymétrique (les efforts de cisaillement et les efforts de traînée ne sont pas représentés). La portance résultante passe par une force ${\overrightarrow{F}}_1$, orientée vers le bas. ${\overrightarrow{F}}_1$ agit sur le point 1 de la ligne de corde. Ce point représente le centre de pression de l'intrados.

Considérons maintenant la pression sur la surface de l'extrados de cette aile. La pression résulte par une force ${\overrightarrow{F}}_2$, orientée en général vers le haut et agissant sur le point 2. Ce point représente le centre de pression de l'extrados.

La force aérodynamique totale sur le profil est obtenue par la somme de ${\overrightarrow{F}}_1$ et ${\overrightarrow{F}}_2$. La portance apparait lorsque $\Vert {\overrightarrow{F}}_2\Vert >\Vert {\overrightarrow{F}}_1\Vert$.

Moment de portance nulle

Dans le cas représenté, puisque ${\overrightarrow{F}}_1$ et ${\overrightarrow{F}}_2$ sont égales et sens opposé, la portance est nulle (et l'incidence est légèrement négative dans le cas d'un profil asymétrique comme celui-ci). C'est pourquoi ce moment de tangage caractéristique du profil est appelé moment de portance nulle, noté $M_0$.

Remarque : Le moment $M_0$ est un couple pur (qui crée de la rotation sans translation). Un couple pur est créé de deux forces égales et opposées dont la ligne d'action de coïncide pas. Une des propriétés mécaniques du couple est l'indépendance du point de référence.

Le centre aérodynamique ou "foyer" du profil

Le centre de pression ne peut être pris comme référence pour l'analyse de la stabilité longitudinale d'un avion car il se déplace avec les variations d'incidence. Plus précisément il avance si l'incidence croit jusqu'au décrochage.

Toutefois, l'analyse de la stabilité peut se faire avec une autre référence qui est le centre aérodynamique. Le centre aérodynamique d’un profil est le point du profil pour lequel le moment est indépendant de l’angle d’incidence (incidence variant dans la plage linéaire de la portance). Ce point est également nommé foyer aérodynamique, point d’application des variations de portance. En effet, la portance en ce point se manifeste lorsque la force de pression résultante de l'extrados est plus grande que la force de pression résultante de l'intrados, c'est-à-dire $\Vert {\overrightarrow{F}}_2\Vert >\Vert {\overrightarrow{F}}_1\Vert$. La portance différentielle s'appliquant en ce point est indépendante du couple créé par le moment de tangage.

Le centre aérodynamique ou "foyer" de l'aile complète

Le centre aérodynamique se situe généralement au quart de la corde aérodynamique moyenne de l'aile, à partir du bord d’attaque pour des vitesses subsoniquesModèle:, (voir Fig. 2).

Coefficient de moment de tangage $C_{M_0}$

La valeur du moment s'exprime par l'équation suivante :

$M_0=\frac{1}{2}\rho {V_T}^{2}Sc{C}_{M_0}$

avec :

$\rho$ : densité de l'air
$V_T$ : vitesse vraie
$\frac{\rho V_T^2}{2}$ : la pression dynamique
$S$ : surface alaire
$c$ : corde moyenne aérodynamique de l'aile ou MAC (Mean Aerodynamic Chord)
$C_{M_0}$ : coefficient de moment de tangage sans dimension typiquement de l'ordre de 0.1.

La valeur du coefficient de moment de tangage $C_{M_0}$ est soit nulle, pour un profil symétrique, soit négative, pour un profil cambré (par convention, un moment en sens horaire est défini comme positif). Cela veut dire qu'au centre aérodynamique, le moment $M_0$ d'un profil asymétrique engendre un couple piqueur.

Remarque: Le fait de cambrer l'aile, par exemple par le braquage de volets hypersustentateurs, entraîne une augmentation du moment inhérent $M_0$, et donc augmente le couple piqueur de l'aile. Le volume d'empennage (défini plus loin) doit être suffisant pour contrer le couple à piquer supplémentaire des volets.

Expressions des portances

Les portances de l'aile $L_W$ (W pour wing, aile) et de l'empennage $L_t$ (t pour tail, empennage) ont pour expressions :

$L_W=\frac{1}{2}\rho {V_T}^{2}S{C}_L{L}_t=k_t\frac{1}{2}\rho {V_T}^2{S}_t{C}_{L_t}$

Modèle:Droite .

Les coefficients de portance

$C_L(\alpha )$ coefficient de portance sans dimension (L pour lift) du profil de l'aile qui dépend de l'incidence $\alpha$
$C_{Lt}(\alpha +\eta )$ coefficient de portance de l'empennage qui dépend de l'incidence de l'empennage qui diffère de celle de l'aile de $\eta$ au gré du pilote.
Les portances varient de façon presque linéaire, typiquement de l'ordre de 0.1 par degré, dans un grand intervalle d'incidence.

$S_t$ est la surface de l'empennage.

Facteur de rendement

L'aile porte en défléchissant une masse d'air vers le bas d'un angle $ϵ$ (appelé en anglais downwash angle) qui est d'autant plus grand que l'incidence est grande. Si l'empennage est dans le sillage de l'aile il reçoit un vent relatif ayant une incidence plus faible $\alpha -ϵ$. Dans une certaine mesure on peut estimer cette déflexion proportionnelle à l'incidence. Ainsi l'incidence effective de l'empennage est une proportion $k_t\alpha$ de l'incidence de l'aile . Le coefficient de portance étant proportionnel à l'incidence, il est donc réduit dans la même proportion.

Ce facteur peut aller jusqu'à 0.5. De nombreux avions et les planeurs récents ont des empennages en position haute, au sommet de la dérive, plus éloignés du sillage de l'aile et d'autant plus efficaces.

Équilibre des moments

Fig. 2 : Forces et moment s'exerçant sur un avion en configuration longitudinale stable
CA indique le centre aérodynamique de l'aile seule qui est pris comme point de référence.
CM indique le centre de masse. Le bras de levier $x$ de la portance de l'aile et la distance $x_{LCA}$ au CA de l'avion au complet (tiret bleu) ont été exagérés pour la clarté du dessin.
L'avion est dessiné à l'horizontale par commodité : les forces sont perpendiculaires à l'avion. La pesanteur n'est pas concernée.

Pour que l'avion garde son attitude (son orientation dans l'espace) la somme des moments des forces aérodynamiques et du poids par rapport au centre de masse CM doit être nulle. L'avion est dit équilibré. Le moment du poids est nul, le centre de masse et le centre de gravité étant confondus. Mettons de côté le moment que peuvent exercer la traînée des ailes et du fuselage et l'action du moteur. Le moment de l'empennage $L_t{l}_t$est celui de sa portance $L_t$ qui s'exerce au foyer de l'empennage, distant de $l_t$ du CM. Il sera à piquer si l'empennage est portant. L'empennage en général symétrique n'a pas de moment de portance nulle. Le moment de l'aile est la somme de celui de sa portance s'exerçant à son foyer CA distant de $x$ du centre de masse et du moment de tangage de l'aile soit $-x{L}_W+M_0$.

Équation des moments

Le moment total par rapport au centre de masse s'écrit :

$M_t(\alpha )=-L_t{l}_t+M_0-x{L}_W$ ,

$M_t(\alpha )=\frac{1}{2}\rho V_T^2(-l_t{k}_t{S}_t{C}_{Lt}(\alpha )+cS{C}_{M0}-xS{C}_L(\alpha ))$Modèle:Droite

On définit

$C_M(\alpha )$

le coefficient de moment total en tangage par

$M_t(\alpha )=\frac{1}{2}\rho V_T^{2}Sc{C}_M(\alpha )$

et le volume d'empennage par

$V_t=\frac{S_t{l}_t}{Sc}$

. On a la relation :

$C_M(\alpha )=-k_t{V}_t{C}_{Lt}(\alpha )+C_{M0}-\frac{x}{c}{C}_L(\alpha )$

Cette équation explicite les contributions au coefficient de moment total.

Le volume d'empennage $V_t$

Le "volume d'empennage " mesure l'importance de l'empennage dans l'équilibre et la stabilité. Il dépend de la surface et du bras de levier de l'empennage, rapportés à la surface et à la corde moyenne de l'aile. Sa valeur est typiquement comprise entre 0.30 et 0.90.

Condition d'équilibre

Fig. 3 : Moment total en noir en fonction de l'incidence, en configuration longitudinale stable.
En bleu le moment de l'empennage, en rouge celui de l'aile.
En pointillé noir le moment total pour une autre position de la gouverne de profondeur.
En ordonnée les moments sans dimension.

Sans action sur la gouverne de profondeur $\eta$=0 l'avion sera équilibré pour l'incidence ${\alpha }_e$ qui annulera le moment de tangage donc le coefficient $C_M({\alpha }_e)$. Pour cette incidence on aura un coefficient de portance adapté à une vitesse donnée. Si le pilote crée une incidence pour l'empennage différente de celle de l'aile il y aura une autre incidence d'équilibre, un autre coefficient de portance pour l'aile principalement et pour l'empennage et donc une autre vitesse, poids et portance de l'avion restant inchangés.

La figure 3 illustre les différents moments (sans dimension) et les incidences d'équilibre.

En bleu le moment de l'empennage $M_{Lt}(\alpha )$. Positif, l'empennage est déporteur, le moment est à cabrer. Le coefficient de portance utilisé obéit à la loi $C_{Lt}(\alpha )=0.08\alpha$ avec l'incidence en degrés, le volume d'empennage choisi est $V_t$ =0.68 et le facteur de rendement est $k_t$=0.9.

En rouge on a le moment de l'aile $M_L(\alpha )$ essentiellement à piquer avec un $C_{M0}=-0.1$ et une loi de portance $C_L(\alpha )=0.11\alpha +0.3$ . Le CM est en arrière du foyer de l'aile avec $x/c=0.3$

En noir est représenté le total, somme de ces deux contributions. L'équilibre existe pour une incidence ${\alpha }_e$= - 0.6°. Le coefficient de portance de l'aile est alors $C_L$ = 0.23 et l'empennage est déportant $C_{Lt}$=- 0.05. Pour avoir une vitesse plus basse, il faut augmenter le coefficient de portance. Pour un braquage à piquer de la profondeur de $\eta$= - 1° l'équilibre a lieu pour une incidence ${\alpha }_e(-1^o)$ = 2.4°. Le coefficient de portance de l'aile est $C_L$=0.57 et l'empennage est portant $C_{Lt}$=0.1. En effet pour cette incidence plus grande, associée à un plus grand coefficient de portance, comme le montre la figure 3, l'empennage devient porteur. Cette portance de l'empennage pour un plus grand coefficient de portance de l'aile s'explique simplement. En allure standard l'empennage est très légèrement déportant ceci signifie que le centre de pression de l'aile est pratiquement au CM. Une augmentation d'incidence donc de coefficient de portance fait avancer le centre de pression, comme cela a été précisé, créant un couple à cabrer qui ne peut être compensé qu'en augmentant la portance de l'empennage créant un couple à piquer. On a la même situation en cas de virage ou le poids apparent augmentant on doit augmenter le coefficient de portance. Voici un exemple :

• Modèle:Unité, Cz global = 0.35, $C_L$ aile = 0.36, $C_{Lt}$ empennage = - 0.04.
• Modèle:Unité, en virage à 60° l'empennage, devient légèrement porteur : Cz global = 0.70, $C_L$ aile = 0.684, $C_{Lt}$ empennage= +0.075.

Stabilité longitudinale

Condition de stabilité statique

Partons d'une situation équilibrée et supposons qu'une perturbation fasse augmenter l'angle d'incidence $\alpha$, si le moment total $M_t$ devient négatif comme c'est le cas sur la figure 3, cela correspond à un moment total piqueur, qui réduit l'incidence générée par la perturbation et tend à la ramener à sa position d'équilibre initiale (le point de convergence ${\alpha }_e(0)$, voir Fig. 3). Ainsi l'avion est stable si la variation de moment est de signe opposé à la variation d'incidence.

$\frac{d{C}_M(\alpha )}{d\alpha }=C_{M\alpha }<0$

On mesure la stabilité en tangage par la valeur de cette dérivée qui sur la figure 3 est $C_{M\alpha }$= - 0.9.

Limite de centrage arrière

Exprimons cette dérivée à partir de l'équation 4

$C_{M\alpha }=\frac{x}{c}\frac{d{C}_L}{d\alpha }-k_t{V}_t\frac{d{C}_{Lt}}{d\alpha }=\frac{d{C}_L}{d\alpha }\frac{x-x_{LCA}}{c}$

en utilisant la “limite de centrage arrière" définie par

$x_{LCA}=c{k}_t{V}_t\frac{d{C}_{Lt}}{d\alpha }/\frac{d{C}_L}{d\alpha }$

qui est la position du foyer aérodynamique ou point neutre de l'avion au complet : distance à partir du foyer de l'aile au foyer de l'avion au complet, voir Fig 2. En effet supposons que le CM soit en ce point, $x=x_{LCA}$ , une variation d'incidence ne fournit aucun moment c'est précisément la définition du foyer. Ainsi l'avion sera stable si $x<x_{LCA}$ c'est-à-dire le CM est en avant du point neutre de l'avion ce qui explique le choix du terme limite de centrage arrière.

La marge statique

La marge statique de l'avion est définie comme la distance entre le centre de masse et la limite de centrage arrière, divisée par la corde moyenne aérodynamique CMA de l'aile $c$. Il s'agit du facteur $\frac{x_{LCA}-x}{c}$ qui s’exprime aussi en % . Elle mesure la stabilité. Si on avance le CM, c'est-à-dire pour une plus grande marge statique, plus grand sera le moment de rappel, plus stable sera l'avion. Dans l'exemple correspondant à la figure 3 la marge statique est 14%. La marge statique est positive quand le centre de masse se trouve devant le point neutre ce qui est le cas d'un avion stable. Mais prenons un avion ayant une CMA de Modèle:Unité avec une marge statique de 10 % . Cela signifie qu'un recul du centre de masse de plus de Modèle:Unité entraînerait une instabilité.

Stabilité et manœuvrabilité

En vol équilibré à l'incidence $\alpha$ pour l'aile et l'empennage supposons que le pilote modifie brutalement l'incidence de l'empennage dans le but de modifier le coefficient de portance de l'aile . Cette modification soudaine de l'incidence de l'empennage va entraîner une variation de son coefficient de portance de $\delta C_{Lt}$ et une modification du moment de l'empennage (équation 4) de

$-k_t{V}_t\delta C_{Lt}$

À cette nouvelle position de la gouverne il y a une nouvelle situation d'équilibre associée à une variation de l'incidence d'équilibre $\delta \alpha$ et du coefficient de portance $\delta C_L$ et comme l'avion est stable cette modification du moment de l'empennage est le couple de rappel donné par la formule 6

$-k_t{V}_t\delta C_{Lt}=\frac{x-x_{LCA}}{c}\frac{d{C}_L}{d\alpha }\delta \alpha =\frac{x-x_{LCA}}{c}\delta C_L$

Ainsi le supplément de moment à assurer par l'empennage pour changer de situation d'équilibre est d'autant plus important que grande est la marge statique. Il se peut même que l'empennage ne puisse assurer un tel moment par suite de décrochage. Ces grands efforts sur l'empennage nuisent à la manœuvrabilité de l'avion. Stabilité et manœuvrabilité s'excluent.

Limites de centrage

Fig. 4 : Plage de centrage d'un Robin DR400

Le chargement de l'avion doit être tel que le CM soit situé entre deux limites de sécurité : la limite de centrage avant et la limite de centrage arrière. L'espace compris entre ces deux limites s'appelle plage de centrage.

• La limite de centrage arrière est, comme vu précédemment, une limite de stabilité. Un centrage arrière diminue la stabilité mais augmente la maniabilité : une faible traction sur le manche peut suffire à provoquer une forte rotation en tangage et à amener très rapidement aux grands angles d'incidence et au décrochage. Le décollage sera spécialement dangereux (sous réserve d'un système de stabilisation automatique).
• La limite de centrage avant est soit une limite de maniabilité (l'avion est stable mais difficile à manœuvrer car la gouverne de profondeur peut manquer de puissance), et/ou une limite de résistance mécanique du train avant. Un centrage très avant peut amener des efforts excessifs sur le train avant, notamment en cas de rebonds à l'atterrissage. Un centrage avant augmente la stabilité mais diminue la maniabilité : le moment piqueur important nécessitera au cours des manœuvres, une traction importante sur le manche pour maintenir une assiette correcte ainsi qu'une vitesse élevée pour rendre la gouverne efficace. Un excès de centrage avant peut rendre impossible le décollage.

Exemple d'un avion d'aéro-club. Les limites de centrage comptent une marge de sécurité définie par le constructeur. Si on prend l'exemple d'un Robin DR400, elles sont mentionnés dans la fiche de centrage et dans le manuel de vol. La limite de centrage arrière ne dépend que de la géométrie de l'avion. Elle est située à Modèle:Unité du point de référence (33 % MAC) sur l’ensemble du domaine des masses. la limite de centrage avant dépend de la catégorie de l'appareil (Normal ou Utilitaire) et de son chargement. La limite de centrage avant est située à Modèle:Unité du point de référence (soit 12 % MAC) pour l'avion non chargé.

Avion-canard et stabilité

Un avion-canard a son empennage à l'avant (!) et l'aile majoritairement porteuse à l'arrière. Que devient l'analyse de l'équilibre et de la stabilité.

• Condition de stabilité : il faut toujours que le CM soit en avant du centre aérodynamique de l'avion au complet de façon qu'une augmentation d'incidence crée un moment de tangage de rappel (équation 5).

Le centre aérodynamique est le « centre de gravité » des suppléments de portance de l'aile $\delta L_W$ avec un bras de levier $x_{LCA}$ et de l'empennage $\delta L_t$ avec un bras de levier $l_t$ pour un changement d'incidence de $\delta \alpha$.

$x_{LCA}\delta L_W=l_t\delta L_t$

ainsi son expression 7 reste inchangée. Il en est de même pour l'expression de la stabilité (formule 8) à la différence qu'un CM en avant de la limite de centrage arrière signifie maintenant $x>x_{LCA}$

Cette limite de centrage arrière est en avant du CA de l'aile (pratiquement $c/4$ du bord d'attaque) de la distance $x_{LCA}$. La stabilité implique que le CM soit encore plus en avant de la quantité qui est la marge statique. Ainsi à la différence de l'avion classique, l'aile seule ne peut plus assurer toute la portance de l'avion, et l'empennage est nécessairement porteur (et déstabilisant : ce n'est pas un empennage).

• Condition d'équilibre définissant la position du CM : bien que dans l'expression 3 il faille inverser tous les signes, l'expression de la condition d'équilibre $C_M(\alpha )=0$ reste inchangée. On note cependant que le centre de pression de l'aile se trouve en arrière de son centre aérodynamique en raison de son moment de portance nulle. Ceci donne un moment à piquer plus important que celui de sa seule portance.

Stabilité artificielle

Dans le cas d'un avion statiquement instable, le centre de masse se trouve derrière le centre aérodynamique. Si une perturbation fait augmenter l'angle d'incidence, le moment résultant de la portance de l'aile, cette fois-ci positif, induit un couple à cabrer, qui est plus important que le couple à piquer de l'empennage. Cela entraîne un moment total $M_t$ positif, à cabrer, qui s'ajoute à la perturbation initiale . Pour sortir de cette situation, une contre-réaction est nécessaire, qui peut être contrôlée par le pilote, mais nécessite de sa part une attention. Si le centrage recule encore, rendant l'avion dynamiquement instable, il peut devenir difficilement contrôlable.

Les commandes de vol électriques permettent de rendre une stabilité artificielle à un avion instable, des calculateurs étant interposés entre les actions du pilote sur le manche et les ordres transmis aux gouvernes. L'Airbus A320 a été le premier avion de ligne à exploiter ce principe. L'avantage d'un tel système est d'autoriser une plage de centrage plus étendue et de diminuer la traînée d'équilibrage (traînée induite par la portance ou la déportance de l'empennage, dont l'envergure donc le rendement aérodynamique est inférieur à celui de l'aile) et la consommation de carburant.

Stabilité dynamique

Fig. 5 : Angles intervenant dans la stabilité d'un avion
Oxa est l'axe de roulis de l'avion, OXw est dirigé le long de la vitesse avec w pour wind, vent.

Supposons que par suite d'une rafale ou d'une action sur la profondeur que l'avion ne soit plus en équilibre des moments. L'avion étant stable il y aura un moment de rappel vers l'incidence d'équilibre correspondant à la position de la profondeur. Ce moment sera proportionnel à la "stabilité" mesuré par $C_{M\alpha }$ et par l'écart à l'incidence d'équilibre. Ce moment de rappel va vouloir mettre l'avion en tangage. Pour comprendre comment va réagir l'avion dans le cas où le pilote n'agit plus sur la profondeur (manche bloqué) il est nécessaire d'introduire d'autres angles que l'incidence. Ils sont illustrés sur la figure 5.

• l'angle d'incidence $\alpha$ est angle entre l'axe de roulis de l'avion et sa vitesse par rapport à l'air. Son écart à sa valeur d'équilibre nous renseigne sur le moment de rappel et sur la variation de portance de l'avion.
• l'angle $\theta =\alpha +\gamma$ de l'avion avec l'horizontale définit l'attitude. C'est lui qui va évoluer sous l'action du moment de rappel.
• l'angle $\gamma$ ou pente aérodynamique est l'angle de la trajectoire ou de la vitesse (à ne pas confondre avec l'axe de l'avion) avec l'horizontale. La modification de portance va incurver la trajectoire, changer sa pente et donc la composante du poids sur la trajectoire. Ceci va entraîner une variation de la vitesse. Ainsi pour un supplément de portance l'avion va "cabrer" et la vitesse va diminuer.

Ainsi l'attitude et la trajectoire sont affectés simultanément après la perturbation initiale. On peut mettre en équations l'évolution de $\theta$, de la pente $\gamma$ et de la vitesse. La solution de ces équations montre que le retour à l'équilibre se fait par une superposition de deux modes d'oscillations, dits modes "propres". Un de ces modes est une oscillation de tangage où la trajectoire est peu affectée, l'autre est une oscillation de trajectoire dite oscillation phugoïde où l'angle d'incidence est peu affecté.

Oscillation de tangage de courte période

En supposant que la trajectoire soit peu affectée, l'attitude et l'incidence sont peu différents $\theta \simeq \alpha$. Le moment de rappel va tendre à mettre l'avion en tangage. Tout changement de vitesse de rotation $\dot{\alpha }$ est affecté par le moment d'inertie de l'avion en tangage $I_y$. Comme un pendule écarté de sa position d'équilibre puis relâché dépasse sa position d'équilibre sous l'effet de son inertie, l'avion va osciller autour de son incidence d'équilibre avec une période d'autant plus grande que son moment d'inertie de tangage est grand et d'autant plus petite que sa stabilité est grande.

Cette oscillation, comme on va le montrer, a une période de quelques secondes et elle peut être amortie au point qu'il n'y a pas d'oscillation du tout. Une cause d'amortissement est assez subtile : l'empennage étant à une distance $l_t$ non négligeable du CM, la vitesse angulaire de tangage $\dot{\alpha }$ va se traduire par une vitesse verticale (plus précisément perpendiculaire à la vitesse de l'avion) de l'empennage de $l_t\dot{\alpha }$. Ainsi le vent que reçoit l'empennage est le vent ressenti par l'aile composé avec cette vitesse verticale. Ceci crée une incidence effective sur l'empennage augmentée de $l_t\dot{\alpha }/V_T$ donc une variation de portance qui n'a pas été prise en compte dans l'approche statique de la stabilité (équation 4) et qui se traduit par l'amortissement de cette oscillation.

On obtient l'ordre de grandeur de la période de cette oscillation en tangage en utilisant le théorème du moment cinétique. La dérivée du moment cinétique par rapport au temps $I_y\ddot{\alpha }$ est égale au moment de tangage :

$I_y\ddot{\alpha }=-\left(\frac{\rho V_T^2}{2}Sc\right)\left|C_{M\alpha }\right|(\alpha +l_t\dot{\alpha }/V_T)$

où on a pris en compte l'incidence effective de l'empennage. Par extension $\alpha$ est l'écart à l'incidence d'équilibre et le signe indique que c'est bien un moment de rappel, l'avion étant stable $C_{M\alpha }$<0. Expression qui s'écrit aussi :

$\ddot{\alpha }+{\omega }_s^2(l_t\dot{\alpha }/V_T+\alpha )=0$

On reconnait l'équation d'un oscillateur harmonique avec un amortissement avec une pulsation ${\omega }_s$ avec s, short pour rappeler qu'il s'agit de l'oscillation de tangage de courte période, donnée par :

${\omega }_s^2=\frac{\rho V_T^2}{2I_y}Sc\left|C_{M\alpha }\right|$ d'autant plus grande que grande est la stabilité et un taux d'amortissement ${\tau }_s=\frac{{\omega }_s{l}_t}{2V_T}$

Pour avoir un ordre de grandeur on peut estimer le moment d'inertie par la masse fois le carré de la corde moyenne aérodynamique CMA de l'aile

$M{c}^2$

et la vitesse en égalant le poids à la portance

$Mg\simeq \frac{1}{2}\rho V_t^{2}S{C}_L$

l'expression ne fait apparaître ni masse, ni moment d'inertie ni vitesse, importe la marge statique par le oefficient de stabilité:

${\omega }_s^2=\frac{g}{c}\frac{\left|C_{M\alpha }\right|}{C_L}$

Estimons $\left|C_{M\alpha }\right|\simeq 2C_L$ et ${\omega }_s\sim \sqrt{2g/c}$ c'est-à-dire de l'ordre du radian par seconde (période de quelques secondes).

L'amortissement est rapide, au bout d'une oscillation l'amplitude est réduite de $e^{-2\pi {\tau }_s}$ de l'ordre de la moitié. Ainsi après quelques oscillations, seule subsistera l'oscillation phugoïde.

Fig. 6 : Schéma des oscillations de tangage en haut: la trajectoire est peu modifiée
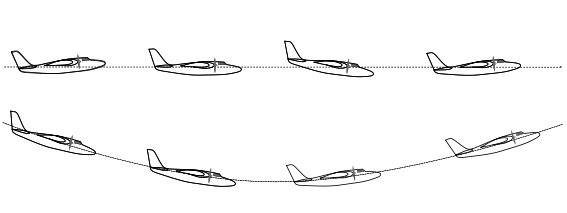
en bas oscillation de trajectoire phugoïde, l'incidence est peu modifiée

Oscillation phugoïde

Cette oscillation a été étudiée et dénommée en 1908 par l'ingénieur anglais Frederick Lanchester. Elle a une période nettement plus longue que l'oscillation de tangage; elle est moins vite amortie. C'est une oscillation qui combine la trajectoire et la vitesse de l'avion, l'incidence de l'avion restant pratiquement inchangée.

Son explication est assez simple. Un déséquilibre initial change l'assiette de l'avion et modifie sa pente aérodynamique. Si par exemple la pente est plus forte, le poids va avoir une composante plus importante sur la trajectoire. L'avion va donc prendre de la vitesse. À une augmentation de vitesse va correspondre une augmentation de portance et donc une force qui incurve la trajectoire vers le haut diminuant la pente jusqu'à la rendre positive. L'énergie potentielle augmente avec l'altitude, l'énergie cinétique diminue avec la vitesse et la portance ne pourra plus compenser le poids. La trajectoire va s'incurver vers le bas et ainsi de suite. Il y aura donc un échange périodique entre énergie potentielle et énergie cinétique qui ne s'amortirait pas sans la traînée qui dissipe cette énergie. On peut ainsi par des considérations d'énergie obtenir les caractéristiques de cette oscillation; on peut utiliser les éléments déjà introduits pour le faire.

En supposant que les variations d'incidence soient négligeables et que le déséquilibre initial se traduise par un déséquilibre de la vitesse, autrement dit que la vitesse s'éloigne de $v$ de la vitesse d'équilibre $V_T$. Portance et traînée, fonction du carré de la vitesse vont donc changer de $\delta L_W=2L_{W}v/V_T$ pour la portance et de $\delta L_D=2L_{D}v/V_T$ pour la traînée (D pour drag).

Le supplément de portance perpendiculaire à la vitesse est une force centripète qui va incurver la trajectoire. Plutôt que d'écrire comme d'habitude l'accélération centripète comme $V_T^2/R$ avec le rayon de courbure il est plus pratique de faire apparaître le changement de pente. On vérifiera qu'elle peut s'écrire aussi $\dot{\gamma }{V}_T$. Le principe fondamental de la dynamique projeté sur la perpendiculaire à la vitesse s'écrit :

$M\dot{\gamma }{V}_T=\delta L_W$

Le supplément de traînée et la modification de la composante du poids sur la trajectoire vont changer la vitesse. Ce même principe fondamental de la dynamique projeté sur la vitesse s'écrit

$M\dot{v}=-\delta L_D-Mg\sin \gamma$

pour aller plus loin il faut estimer la portance par le poids comme précédemment et la traînée à partir de la portance en utilisant la finesse $L_D=L_W/f$ et l'approximation du sinus par l'arc.

En dérivant par rapport au temps l'équation 13 et en utilisant l'équation 12 on arrive à l'équation pour la variation de vitesse

$\ddot{v}=-\frac{2g}{f{V}_T}\dot{v}-\frac{2g^2}{V_T^2}v$

qui est l'équation caractéristique d'un oscillateur amorti (voir amortissement physique). C'est la même équation qui va gouverner la pente aérodynamique $\gamma$.

Sa période est $T_{ph}=\frac{2\pi }{\sqrt{2}}\frac{V_T}{g}$ ce qui est une bonne estimation . Elle est nettement plus grande que celle de l'oscillation de tangage. Le taux d'amortissement est $\tau =1/(f\sqrt{2})$. Ainsi pour un avion volant à Modèle:Unité (Modèle:Unité) de finesse 20 la période est d'environ 45 s et l'amplitude après une période est réduite seulement d'un facteur $e^{-2\pi \tau }$=80%. Cette oscillation est généralement bien contrôlée par le pilote.

Bibliographie

• Malcolm J. Abzug, E. Eugene Larrabee (2002) : Airplane Stability and Control : A History of the Technologies That Made Aviation Possible, Cambridge Aerospace Series, Modèle:ISBN, Modèle:ISBN
• Almond, P. (1997) : Aviation - The Early Years, Könemann Verlagsgesellshaft mbH, Modèle:ISBN * Peyrat-Armandy, A. (1997) : Les avions de transport modernes et futurs, Teknea Modèle:ISBN

Articles connexes

• Stabilité (aéronautique)
• Aérodynamique
• Configuration générale d'un aéronef