Théorème des restes chinois

En mathématiques, le théorème des restes chinois est un résultat d'arithmétique modulaire traitant de résolution de systèmes de congruences. Ce résultat, initialement établi pour ℤ/nℤ, se généralise en théorie des anneaux. Ce théorème est utilisé en théorie des nombres.

Fragments d'histoire

Exemple de Sun Zi : il y a 23 objets.

Exemple de Sun Zi

La forme originale du théorème apparait sous forme de problème dans le livre de Sun Zi, le Modèle:Lien, datant du Modèle:IIIe siècle. Il est repris par le mathématicien chinois Qin Jiushao dans son ouvrage le Shùshū Jiǔzhāng (« Traité mathématique en neuf chapitres ») publié en 1247. Le résultat concerne les systèmes de congruences (voir arithmétique modulaire).

Soient des objets en nombre inconnu. Si on les range par 3 il en reste 2. Si on les range par 5, il en reste 3 et si on les range par 7, il en reste 2. Combien a-t-on d'objets ?

Cette énigme est parfois associée au général Modèle:Lien comptant son armée.

La résolution proposée par Sun Zi pour ce problème est la suivante :

Multiplie le reste de la division par 3, c’est-à-dire 2, par 70, ajoute-lui le produit du reste de la division par 5, c’est-à-dire 3, avec 21 puis ajoute le produit du reste de la division par 7, c'est-à-dire 2 par 15. Tant que le nombre est plus grand que 105, retire 105.

Mais la solution n'explique qu'imparfaitement la méthode utilisée. On peut cependant remarquer que :

• 70 a pour reste 1 dans la division par 3 et pour reste 0 dans les divisions par 5 et 7 ;
• 21 a pour reste 1 dans la division par 5 et pour reste 0 dans les divisions par 3 et 7 ;
• 15 a pour reste 1 dans la division par 7 et pour reste 0 dans les divisions par 3 et 5.

Le nombre $233(2\times 70+3\times 21+2\times 15)$ a bien alors pour restes respectifs 2, 3 et 2 dans les divisions par 3, 5 et 7. Enfin, comme 105 (3×5×7) a pour reste 0 dans les trois types de division, on peut l’ôter ou l'ajouter autant de fois que l'on veut sans changer les valeurs des restes. La plus petite valeur pour le nombre d'objets est alors de 23.

On retrouve ce problème presque à l'identique en 1202 dans le Liber Abbaci de Fibonacci dans le chapitre XII qui concerne les problèmes et énigmes où l'on trouve également le problème des lapins de la suite de Fibonacci. Le problème avait aussi été étudié par Ibn al-Haytham (Alhazen) – voir l'article Mathématiques arabes – dont Fibonacci a pu lire les œuvres.

Euler s'est également intéressé à cette question, ainsi que Gauss.

Astronomie

Selon Modèle:Lien, la motivation de ce type de calcul chez les Chinois serait l'astronomie. On peut en effet penser que les Chinois, férus de calculs astronomiques, puissent être intéressés par des concordances de calendrier et qu'ils aient été amenés très tôt à s'intéresser à des questions du type :

Dans combien de jours la pleine lune tombera-t-elle au solstice d'hiver ?

Si la question se pose alors qu'il reste 6 jours avant le solstice d'hiver et 3 jours avant la pleine lune, la question se traduit par :

Existe-t-il un entier x tel que le reste de la division de x par 365 donne 6 et le reste de la division de x par 28 donne 3 ?

Comptage de paquets

Mais selon Daumas et al., il s'agirait plus probablement de problèmes associés à des comptages par paquets, peut-être d'origine divinatoire.

Enfin, il serait dommage de ne pas présenter ce problème concernant des pirates et un trésor, très fréquemment cité pour illustrer le théorème des restes chinois :

Une bande de 17 pirates possède un trésor constitué de pièces d'or d'égale valeur. Ils projettent de se les partager également, et de donner le reste au cuisinier chinois. Celui-ci recevrait alors 3 pièces. Mais les pirates se querellent, et six d'entre eux sont tués. Un nouveau partage donnerait au cuisinier 4 pièces. Dans un naufrage ultérieur, seuls le trésor, six pirates et le cuisinier sont sauvés, et le partage donnerait alors 5 pièces d'or à ce dernier. Quelle est la fortune minimale que peut espérer le cuisinier s'il décide d'empoisonner le reste des pirates ?

La réponse est 785. Les nombres 17, 11 et 6 étant premiers entre eux deux à deux, les solutions sont distantes d'un multiple de 1122 (17×11×6) ; par ailleurs 785 vérifie bien l'énoncé : 785 = 17×46 + 3 = 11×71 + 4 = 6×130 + 5. Il s'ensuit que 785 est bien le plus petit des nombres possibles.

L'arithmétique modulaire a rendu ce type de problème plus facile à résoudre.

Système de congruences d'entiers

Théorème

Soient $n_1,\dots ,n_k$ des entiers deux à deux premiers entre eux, c'est-à-dire que $\text{PGCD}$$(n_i,n_j)=1$ lorsque $i\ne j$. Alors pour tous entiers $a_1,\dots ,a_k$, il existe un entier $x$, unique modulo $n=\prod _{i=1}^k{n}_i$, tel que

$\{\begin{array}{c}x\equiv a_1(\mathrm{mod}{n}_1)\\ ⋮\\ x\equiv a_k(\mathrm{mod}{n}_k)\end{array}$

Algorithme

Une solution $x$ peut être trouvée comme suit. Pour chaque i, les entiers $n_i$ et ${\hat{n}}_i=\frac{n}{n_i}=n_1\dots n_{i-1}{n}_{i+1}\dots n_k$ sont premiers entre eux. D'après le théorème de Bachet-Bézout on peut calculer l'inverse $v_i$de ${\hat{n}}_i$ modulo $n_i$. Pour cela, on peut utiliser l'algorithme d'Euclide étendu et obtenir des entiers $u_i$ et $v_i$ tels que $u_i{n}_i+v_i{\hat{n}}_i=1$. Si on pose $e_i=v_i{\hat{n}}_i$, alors nous avons

$e_i\equiv 1(\mathrm{mod}{n}_i)$ et $e_i\equiv 0(\mathrm{mod}{n}_j)$ pour j ≠ i.

Une solution particulière de ce système de congruences est par conséquent

$x=\sum _{i=1}^k{a}_i{e}_i,$

et les autres solutions sont les entiers congrus à $x$ modulo le produit $n$.

Exemple

L'exemple de Sun Zi, présenté plus haut dans la section histoire, se réduit à

$x\equiv 2(\mathrm{mod}3)$

$x\equiv 3(\mathrm{mod}5)$

$x\equiv 2(\mathrm{mod}7)$

on obtient alors

• $n=3\times 5\times 7=105$
• $n_1=3$ et ${\hat{n}}_1=5\times 7=35$ , or $2{\hat{n}}_1\equiv 1(\mathrm{mod}3)$ donc $e_1=70$
• $n_2=5$ et ${\hat{n}}_2=3\times 7=21$ , or ${\hat{n}}_2\equiv 1(\mathrm{mod}5)$ donc $e_2=21$
• $n_3=7$ et ${\hat{n}}_3=3\times 5=15$ , or ${\hat{n}}_3\equiv 1(\mathrm{mod}7)$ donc $e_3=15$

une solution pour $x$ est alors $x=2\times 70+3\times 21+2\times 15=233$

et les solutions sont tous les entiers congrus à 233 modulo 105, c'est-à-dire à 23 modulo 105.

Généralisation à des nombres non premiers entre eux

Les systèmes de congruences peuvent être résolus même si les n_i ne sont pas premiers entre eux deux à deux. Le critère précis est le suivant : Modèle:Énoncé Exemple : le système $x\equiv -1[4]$ et $x\equiv -1[6]$ équivaut à : $x+1$ multiple de $4$ et $6$ c'est-à-dire de $\text{PPCM}(4,6)=12$, ou encore : $x\equiv -1(\mathrm{mod}12)$

Une méthode de résolution de tels systèmes est la méthode chinoise, qui consiste à se ramener à des modules premiers entre eux deux à deux (dans l'exemple ci-dessus : les modules 4 et 3). Une autre est la méthode des substitutions successives.

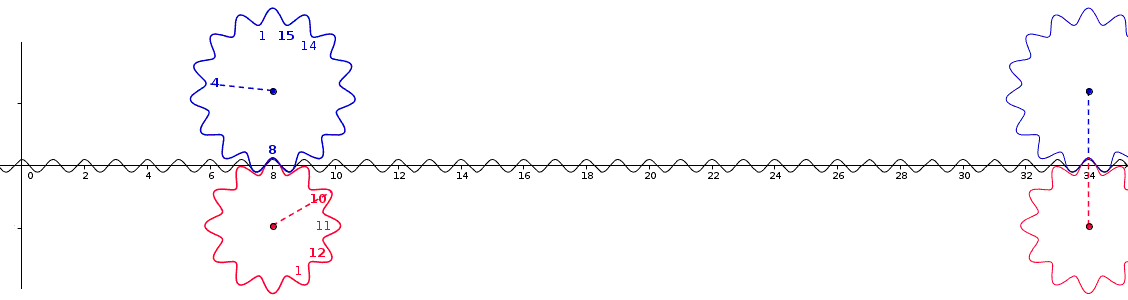
Interprétation mécanique

La résolution du système $\{\begin{array}{c}x\equiv r(\mathrm{mod}a)\\ x\equiv s(\mathrm{mod}b)\end{array}$  , d'inconnue $x$ , passe par le calcul du PPCM de $a$ et $b$.

Une roue dentée comportant $a$ dents s'engrène dans une autre roue dentée comportant elle $b$ dents. Combien de dents doivent passer pour que sa $r$-ième dent vienne en coïncidence avec la $s$-ième dent ?

Le PPCM des deux nombres $a$ et $b$ est ce qui permet de comprendre le comportement périodique de ce système : c'est le nombre de dents séparant deux contacts de même congruence. On peut donc trouver la solution, s'il y en a une, dans l'intervalle $[1,\mathrm{P}\mathrm{P}\mathrm{C}\mathrm{M}\mathrm{(}\mathrm{a},\mathrm{b}\mathrm{)}\mathrm{]}$. Il y a une solution si PGCD(a, b) divise r – s .

Pour cet engrenage, $\{\begin{array}{c}x\equiv 4(\mathrm{mod}15)\\ x\equiv 10(\mathrm{mod}12)\end{array},\text{PPCM}(12,15)=60$ pour $x\in [1,60]$ , la solution est $x=34$.

On peut comprendre simplement pourquoi le calcul sur des roues dentées fait intervenir de l'arithmétique modulaire, en remarquant que l'ensemble des dents d'une roue en comptant n peut être paramétré par l'ensemble des racines n-ièmes de l'unité, qui a une structure de groupe naturellement isomorphe à celle de ℤ/nℤ.

Résultat pour les anneaux

Dans les anneaux Z/nZ

Le théorème chinois a également une version plus abstraite : si Modèle:Math, …, Modèle:Math sont deux à deux premiers entre eux alors, en notant Modèle:Math le PPCM des Modèle:Math, c'est-à-dire dans le cas présent le produit des Modèle:Math, l'application (à valeurs dans l'anneau produit)

$\begin{array}{cccc}\varphi :& \mathbb{Z}/n\mathbb{Z}& ⟶& \mathbb{Z}/n_1\mathbb{Z}\times \cdots \times \mathbb{Z}/n_k\mathbb{Z}\\ & \alpha [n]& ⟼& (\alpha [n_1],\dots ,\alpha [n_k])\end{array}$

est un isomorphisme d'anneaux.

Par exemple, la table suivante compare $\mathbb{Z}/15\mathbb{Z}$ et $\mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/5\mathbb{Z}$ et chaque paire d'éléments de $\mathbb{Z}/3\mathbb{Z}\times \mathbb{Z}/5\mathbb{Z}$ apparaît exactement une et seule fois :

x	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
x mod 3	0	1	2	0	1	2	0	1	2	0	1	2	0	1	2
x mod 5	0	1	2	3	4	0	1	2	3	4	0	1	2	3	4

Pour le montrer, on remarque d'abord que les deux ensembles finis $\mathbb{Z}/n\mathbb{Z}$ et $\mathbb{Z}/n_1\mathbb{Z}\times \cdots \times \mathbb{Z}/n_k\mathbb{Z}$ ont le même nombre d'éléments. Comme $\varphi$ est un morphisme d'anneaux, il suffit donc de démontrer qu'il est injectif pour en déduire que c'est un isomorphisme. Pour cela, il suffit de montrer que son noyau est réduit à 0 : si $\alpha \equiv 0mod{n}_i$ pour $i=1,\dots ,k$, c’est-à-dire si $\alpha$ est un multiple de chaque Modèle:Math, alors $\alpha \equiv 0modn$, c’est-à-dire $\alpha$ est un multiple du produit $n_1,\dots ,n_k$. Ceci résulte de l'hypothèse que les $n_i$ sont premiers entre eux deux à deux.

Dans le [[#Généralisation à des nombres non premiers entre eux|cas où les Modèle:Math ne sont pas deux à deux premiers entre eux]], le morphisme ci-dessus n'est qu'injectif. Il existe une solution au problème initial si et seulement si les données sont dans l'image, c'est-à-dire que le pgcd de $n_i$ et $n_j$ divise $a_i-a_j$ pour tout couple $(i,j)$.

Dans un anneau principal

Pour un anneau principal R, le théorème des restes chinois prend la forme suivante : Si r₁, …, r_k sont des éléments de R qui sont premiers entre eux deux à deux, et r désigne le produit r₁…r_k, alors le morphisme d'anneaux

$\begin{array}{cccc}f:& R/rR& ⟶& R/r_{1}R\times \cdots \times R/r_{k}R\\ & x\mathrm{m}\mathrm{o}\mathrm{d}rR& ⟼& (x\mathrm{m}\mathrm{o}\mathrm{d}{r}_{1}R,\cdots ,x\mathrm{m}\mathrm{o}\mathrm{d}{r}_{k}R)\end{array}$

est un isomorphisme.

L'isomorphisme inverse peut être construit comme ceci. Pour chaque i, les éléments r_i et r / r_i sont premiers entre eux et par conséquent, il existe des éléments u_i et v_i dans R tels que

$u_i{r}_i+v_i{\frac{r}{r}}_i=1$

Fixons e_i = v_i r / r_i. On a :

$e_i\equiv 1(\mathrm{mod}{r}_i)\mathrm{e}\mathrm{t}{e}_i\equiv 0(\mathrm{mod}{r}_j)$

pour j ≠ i.

Alors l'inverse de Modèle:Math est le morphisme construit à l'aide des idempotents eModèle:Ind (mod r) :

$\begin{array}{cccc}g:& R/r_{1}R\times \cdots \times R/r_{k}R& ⟶& R/rR\\ & (a_1\mathrm{m}\mathrm{o}\mathrm{d}{r}_{1}R,\cdots ,a_k\mathrm{m}\mathrm{o}\mathrm{d}{r}_{k}R)& ⟼& \sum _{i=1}^k{a}_i{e}_i\mathrm{m}\mathrm{o}\mathrm{d}rR.\end{array}$

Exemple des polynômes

Le théorème des restes chinois permet de résoudre explicitement tout système de congruences dans l'anneau euclidien R = K[X] des polynômes sur un corps K, c'est-à-dire tout système de la forme.

où les données sont des polynômes RModèle:Ind deux à deux premiers entre eux et des polynômes AModèle:Ind, et l'inconnue est le polynôme P.

L'interpolation lagrangienne correspond au cas particulier où les RModèle:Ind sont de la forme X – xModèle:Ind et les AModèle:Ind sont constants, et fournit la solution P de degré ≤ n . Plus explicitement, si xModèle:Ind, xModèle:Ind, … , xModèle:Ind sont n + 1 éléments de K distincts deux à deux, on prend pour E_i les polynômes interpolateurs de Lagrange, définis par : Modèle:Retrait Pour j différent de i, E_i est divisible par R_j, de sorte que E_i ≡ 0 modulo R_j. Par ailleurs, modulo R_i, X ≡ x_i, de sorte que E_i ≡ 1 modulo R_i.

Pour n + 1 éléments quelconques yModèle:Ind, yModèle:Ind, … , yModèle:Ind de K, dire qu'un polynôme P est tel que P(x_i) = y_i pour tout i, est équivalent à dire que P ≡ y_i modulo R_i. Un tel polynôme P est donné par Modèle:Retrait ce qu'on peut vérifier par un calcul direct.

Subtilité dans les anneaux factoriels

La preuve du théorème chinois repose sur l'existence d'une relation de Bézout. Dans les anneaux factoriels, il n'est pas toujours possible de faire le lien entre le fait que deux éléments soient premiers entre eux, et l'existence d'une relation de Bézout. Considérons par exemple l'anneau factoriel $\mathbb{Z}[X]$ (il est factoriel car un anneau de polynômes sur un anneau factoriel est toujours factoriel, ce qui est un corollaire du lemme de Gauss sur le contenu).

On constate que $2$ et $X$ sont deux éléments de $\mathbb{Z}[X]$ premiers entre eux. En effet, soit $Q$ un diviseur commun. Le fait que $Q\mid 2$ se traduit par l'existence d'un $R\in \mathbb{Z}[X]$ tel que $QR=2$, ce qui implique que $Q$ est constant, valant $\pm 1$ ou $\pm 2$. Le fait que $Q\mid X$ implique que $Q$ ne peut pas valoir $\pm 2$. Ainsi, $2$ et $X$ sont bien premiers entre eux.

On serait tenté de partir de cette dernière remarque pour appliquer le théorème chinois. Cela impliquerait, par exemple, l'existence d'un élément $P\in \mathbb{Z}[X]$ tel que $P\equiv 0[2]$ et $P\equiv 1[X]$. La première relation donnerait un élément $Q\in \mathbb{Z}[X]$ tel que $P=2Q$ donc $P(0)$ est un nombre pair. Or, la seconde relation impliquerait que $P(0)=1$, ce qui est contradictoire.

La raison à cette contradiction est que les éléments $2$ et $X$ sont, certes, premiers entre eux (i.e., pas de facteur commun) mais les idéaux $(2)$ et $(X)$ ne sont pas premiers entre eux. En effet, leur somme n'est pas égale à $\mathbb{Z}[X]$. Plus précisément, $(2)+(X)=\{XP+2n\mid P\in \mathbb{Z}[X],n\in \mathbb{Z}\}$. Cela prouve qu'il n'y a pas de relation de Bézout entre ces deux $2$ et $X$.

Remarque : on pourrait remplacer le nombre $2$ par n'importe quel nombre entier différent de 0, 1 ou -1, et ce contre-exemple fonctionnerait verbatim.

Dans les corps munis de valuations indépendantes

Le théorème des restes chinois s'étend de plusieurs façons aux corps munis d'un certain nombre de valuations indépendantesModèle:,, tels que les anneaux factoriels (et a fortiori principaux), les anneaux de Dedekind etc. On le trouve alors sous le nom de « Modèle:Lien » :

Soient $v_1,v_2,\dots ,v_n$ des valuations discrètes indépendantes d'un corps $K$ , $a_1,a_2,\dots ,a_n$ des éléments de $K$, et $k_1,k_2,\dots ,k_n$ des entiers relatifs. Alors il existe $x\in K$ tel que $v_i(x-a_i)=k_i$ pour tout $i$.

Le théorème reste vrai pour les valuations non discrètes, en remplaçant les $k_i$ par des éléments du groupe des valeurs des $v_i$.

Le théorème ne suppose pas que les aModèle:Ind soient éléments d'un anneau, ni que les kModèle:Ind soient positifs. Par contre, même si les valuations sont issues d'un anneau (intègre) A, x ne peut être supposé élément de A.

Voyons ce que le théorème signifie pour les rationnels en général lorsque les kModèle:Ind sont positifs, les valuations en jeu étant les valuations p adiques. Si q dénote un nombre rationnel, convenons ici, par homologie avec le cas entier, que q est multiple d'un entier n si le numérateur de q l'est, et si le dénominateur de q est premier avec n. Convenons encore de noter $q_1=q_2[n]$ si $q_1-q_2$ est multiple de $n$ (on peut facilement vérifier que les principes de base des congruences fonctionnent encore pour cette dȩfinition étendue, à quelques adaptations près).

Le théorème d'approximation faible implique alors que si nModèle:Ind, nModèle:Ind, ... nModèle:Ind sont r entiers premiers deux à deux, et qModèle:Ind, qModèle:Ind, ... qModèle:Ind sont r rationels, alors il existe un rationnel q tel que q = qModèle:Ind mod nModèle:Ind pour tout i (ce qui est loin de se déduire trivialement du théorème des restes chinois).

On va maintenant faire voir que ce théorème implique le théorème des restes chinois dans $\mathbb{Z}$, et même dans les anneaux principaux. En fait, il est même un peu plus général, car il fournit un élément x de valuation pModèle:Ind-adique exactement égale aux kModèle:Ind.

Supposons donc que A soit un anneau principal, de corps de fractions K. Avec les notations du début de l'article, si les nModèle:Ind sont décomposés en produit de puissances de facteurs premiers pModèle:IndModèle:IndModèle:Exp, on voit facilement, en répétant éventuellement les aModèle:Ind correspondants, qu'il suffit de supposer que nModèle:Ind est une puissance d'un certain élément premier pModèle:Ind, disons pModèle:IndModèle:Exp.

En notant vModèle:Ind les valuations pModèle:Ind-adiques correspondantes, le théorème d'approximation faible dit qu'il existe un élément x de K tel que Modèle:Nobr pour tout i. Notons x = r/s, où r et s sont des éléments de A premiers entre eux. On a donc

$\frac{r}{s}-a_i=p_i^{c_i}q,q\in K,$

les numérateurs et dénominateurs de q n'étant pas multiples de pModèle:Ind. Multiplions cette équation par s, puis regardons la modulo pModèle:IndModèle:Exp :

$s{a}_i=r\mathrm{m}\mathrm{o}\mathrm{d}{p}_i^{c_i}.$

Cela implique que s n'est pas multiple de pModèle:Ind pour tout i, puisque r est premier avec s. Il existe donc t dans A tel que $st=1\mathrm{m}\mathrm{o}\mathrm{d}{p}_1^{c_1}\cdots p_n^{c_n}$. En multipliant la congruence précédente par t, on obtient $a_i=rt\mathrm{m}\mathrm{o}\mathrm{d}{p}_i^{c_i}$ pour tout i; donc rt satisfait aux conditions du théorème des restes chinois.

Observons pour finir que le théorème d'approximation faible n'est pas englobé par le théorème chinois dans les anneaux généraux, exposé dans la section suivante, car les idéaux premiers associés aux valuations ne réalisent pas nécessairement la condition de Bezout; un exemple simple est l'anneau factoriel $\mathbb{Z}[X]$, où l'on a les ideaux premiers $<p>$ et $<X>$, p un nombre premier quelconque, mais $<p>+<X>=\mathbb{Z}[X]$.

Résultat pour les anneaux généraux

Si R est un anneau et I₁, …, I_k des idéaux bilatères de R deux à deux premiers entre eux (ce qui signifie que I_i + I_j = R lorsque i ≠ j), on démontre (par récurrence sur k) que le morphisme

$\begin{array}{ccc}R/(I_1\cap \cdots \cap I_k)& ⟶& R/I_1\times \cdots \times R/I_k\\ x\mathrm{m}\mathrm{o}\mathrm{d}{I}_1\cap \cdots \cap I_k& ⟼& (x\mathrm{m}\mathrm{o}\mathrm{d}{I}_1,\cdots ,x\mathrm{m}\mathrm{o}\mathrm{d}{I}_k)\end{array}$

est un isomorphisme et que l'idéal intersection de ces idéaux est égal à la somme de tous leurs produits dans n'importe quel ordre :

$I_1\cap \cdots \cap I_k=\sum _{\sigma \in {𝔖}_k}{I}_{\sigma (1)}\cdots I_{\sigma (k)}.$

Si l'anneau est commutatif, tous ces produits sont égaux et l'intersection des I_i est simplement égale à leur produit. Mais s'il ne l'est pas, pour deux idéaux bilatères I et J premiers entre eux, en général $I\cap J\ne IJ$, et l'on a seulement $I\cap J=IJ+JI$, d'où l'expression ci-dessus, avec une somme indexée par le groupe symétrique.

Si R est un anneau commutatif général, rien n'autorise à supposer que les idéaux sont co-premiers, même si R est intègre et que ces idéaux sont premiers. Cependant, on peut se demander si le théorème chinois généralisé (Modèle:C.-à-d. qui ne suppose pas les nModèle:Ind premiers entre eux, mais impose des conditions sur les aModèle:Ind) aurait lieu.

C'est justement le cas des Modèle:Lien et en réalité, cette propriété les caractérise. Plus précisémentModèle:,, pour qu'un anneau commutatif intègre soit de Prüfer, il faut et il suffit qu'un système de congruences $x=x_i\mathrm{m}\mathrm{o}\mathrm{d}{I}_i$ admette des solutions dès que $x_i\equiv x_j\mathrm{m}\mathrm{o}\mathrm{d}(I_i+I_j).$

Évidemment, si les idéaux IModèle:Ind sont co-premiers, l'idéal IModèle:Ind + IModèle:Ind est R tout entier, donc la condition sur xModèle:Ind et xModèle:Ind est toujours vérifiée, et le système de congruence a une solution x. On retrouve bien le théorème chinois, tel qu'exposé au début de cette section.

Applications

Des applications du théorème des restes chinois se rencontrent dans la branche diophantienne de la théorie des congruences.

Le théorème suivant peut être vu soit comme une application du théorème des restes chinois, soit comme une généralisation de ce théorème.

Soit $P_i(x_1,x_2,\dots ,x_n)\equiv 0\left[m_i\right]$ avec $i\in \{1,2,\dots ,k\}$ un système de $k$ congruences, où les $P_i$ sont des polynômes de $n$ variables, et où les modules $m_i$ sont premiers deux à deux. Alors ces congruences sont conjointement solvables si et seulement si chacune d'entre elles est solvable séparément; plus précisément, si m est le produit des modules $m_i$, chaque n-uplet $(x_1,x_2,\dots ,x_n)$ où $x_i$ est une solution de la i-ème congruence, détermine bijectivement un n-uplet Modèle:Nobr modulo m satisfaisant toutes les congruences à la fois.

De plus, si l'on convient d'appeler "primitive" une solution Modèle:Nobr d'une congruence telle que chacun des xModèle:Ind soit premier avec le module mModèle:Ind, alors le théorème précédent reste vrai si on le restreint aux solutions primitives: Les congruences sont conjointement primitivement solvables si et seulement si chacune d'entre elles l'est séparément, et il y a bijection entre les n-uplets de solutions primitives modulo mModèle:Ind, et ceux de solutions primitives conjointes modulo m.

La preuve de ce théorème est simple : une solution conjointe induit évidemment une solution pour chaque équation séparément, et inversement, à partir de telles solutions, on reconstruit une solution conjointe avec le théorème des restes chinois.

Évidemment, si $P_i(x)=x-a_i$, on retrouve le théorèmes des restes chinois.

Un autre théorème notoire est le suivant :

Soit $P(x_1,x_2,\dots ,x_n)\equiv 0[m]$ une congruence, où $P$ est un polynôme de $n$ variables, et supposons que $m$ soit le produit de $k$ modules $m_i$ premiers deux à deux. Alors cette congruence est solvable (resp. primitivement solvable) modulo m si et seulement si elle est solvable (resp. primitivement solvable) modulo chaque mModèle:Ind. À nouveau, il y a bijection entre les solutions de la première congruence modulo m et les k-uplets de solutions de congruences modulo chaque mModèle:Ind. La preuve est similaire à celle du théorème précédent.

Grâce à ce dernier théorème, la solution d'une congruence modulo m se réduit a celle des solutions modulo chacune des puissances maximales de facteurs premiers Modèle:Nobr

Parmi les nombreuses applications du théorème des restes chinois à la théorie des nombres, citons encore la démonstration de la multiplicativité de l'indicatrice d'Euler.

Une méthode connexe

On a vu qu'une des applications majeures du théorème des restes chinois résidait dans le fait que la résolution d'une congruence modulo un nombre m, produit de deux nombres mModèle:Ind et mModèle:Ind, se réduisait à la résolution de cette même congruence modulo mModèle:Ind et mModèle:Ind, lorsque mModèle:Ind et mModèle:Ind sont premiers entre eux. Typiquement, les mModèle:Ind sont des puissances de nombres premiers, le théorème chinois étant poussé le plus loin possible. Cela simplifie déjà considérablement les problèmes théoriques et pratiques, mais comment réduire la question plus encore ? La technique suivante est déjà utilisée par Gauss dans les Disquisitiones arithmeticae. Pratiquée avec habileté, le plus souvent par le biais d'une descente infinie, elle permet une analyse fine des cas où les nombres mModèle:Ind et mModèle:Ind ne sont pas premiers entre eux, et de ramener finalement la question aux moduli premiers.

Soit $P(x_1,x_2,\dots x_n)\equiv 0modm$ une congruence, où $P$ est un polynôme de n variables, et m est le produit de mModèle:Ind et mModèle:Ind, non nécessairement premiers entre eux. La résolution de cette congruence équivaut à la résolution successive de $P(x{\text{'}}_1,x{\text{'}}_2,\dots ,x{\text{'}}_n)\equiv 0mod{m}_1$ puis de $Q(x^{\prime }{\text{'}}_1,x^{\prime }{\text{'}}_2,\dots ,x^{\prime }{\text{'}}_n)\equiv 0mod{m}_2$ où le polynôme Q à coefficients entiers est égal à

$Q(X_1,\dots ,X_n)=\frac{1}{m_1}P(m_1{X}_1+x{\text{'}}_1,\dots ,m_1{X}_n+x{\text{'}}_n)$.

L'ensemble des solutions est alors $\{(x_i)=(x{\text{'}}_i+m_1{x}^{\prime }{\text{'}}_i),(x{\text{'}}_i)\in S_1,(x^{\prime }{\text{'}}_i)\in S_2\},$ où $S_1$ et $S_2$ sont les ensembles de solutions des congruences ci-dessus resp.

Modèle:Démonstration/début Si la proposée a une solution $x_i$ modulo m, alors cette solution est évidemment une solution modulo mModèle:Ind. On peut donc poser $x_i=x{\text{'}}_i+m_1{x}^{\prime }{\text{'}}_i$, où $(x{\text{'}}_i)$ est une solution de la proposée modulo mModèle:Ind, et $x^{\prime }{\text{'}}_i$ est un nombre entier déterminé par $x{\text{'}}_i$ et $x_i$. Ainsi, les $x^{\prime }{\text{'}}_i$ vérifient $R(x^{\prime }{\text{'}}_i)=0modm,$ avec $R=P(x{\text{'}}_i+m_1{X}_i).$ Mais il est facile de voir que tous les coefficients du polynôme R sont multiples de mModèle:Ind. On peut donc simplifier cette dernière congruence par mModèle:Ind, ce qui donne $Q(x^{\prime }{\text{'}}_i)=0mod{m}_2$ (notations de l'énoncé).

Réciproquement, supposons qu'il existe une solution de la congruence $P(x_i)=0mod{m}_1,$ et une autre de la congruence $Q(x^{\prime }{\text{'}}_i)=0mod{m}_2,$ Q étant défini à partir de P et $(x_i)$ comme précédemment. Alors en remontant l'argument précédent, on voit que $(x_i=x{\text{'}}_i+m_1{x}^{\prime }{\text{'}}_i)$ est une solution de la proposée.

Exemples :

• Donnons-nous un nombre premier impair p, un entier positif n, et un nombre Modèle:Mvar premier avec p. Soit à démontrer (sans utiliser de racine primitive modulo p) que [[Résidu quadratique#Modulo une puissance d'un nombre premier|Modèle:Mvar est résidu quadratique modulo pModèle:Exp si c'est un résidu quadratique modulo p]] (la réciproque est triviale).

On suppose par récurrence le résultat vrai pour n = N > 0, puisqu'il est trivialement vérifié pour n = 1. En faisant

$P(X)=X^2-a,m_1=p^n\text{et}{m}_2=p$

dans le lemme ci-dessus, on obtient d'abord

$P(x^{\prime })=x{\text{'}}^2-a\equiv 0mod{p}^n$,

qui a bien une solution $x^{\prime }$ par l'hypothèse de récurrence, d'ailleurs première avec p puisque $a$ l'est. Puis

$Q(x^{″})=p^N{x}^{\prime }{\text{'}}^2+2x^{\prime }{x}^{″}+\frac{x{\text{'}}^2-a}{p^N}\equiv 0modp$,

qui n'est autre qu'une équation linéaire modulo p, et a donc une solution $x^{″}$ puisque p est premier avec $2x^{\prime }$. Donc la congruence $x^2-a\equiv 0$ a lieu pour le modulo $m_1{m}_2=p^{n+1}$, et pour tout modulo $p^k$ en général.

• [[Résidu quadratique#Modulo une puissance d'un nombre premier|Tout entier Modèle:Mvar congru à 1 modulo 8 est résidu quadratique modulo 2Modèle:Exp]], $n\in \mathbb{N}$ (réciproque immédiate pour n > 2 et Modèle:Mvar impair).

La séparation $m_1=2^{n-1}$ et $m_2=2$ mène à une tautologie. Mais en observant que le résultat est immédiat pour $n\le 3$, les carrés impairs étant toujours congrus à 1 modulo 8, on prend la séparation $m_1=2^{n-2}$ et $m_2=4$, et on suppose le résultat vrai pour tout $n<N$, avec $N>3$. Soit donc $n=N$. L'hypothèse d'induction fournit une solution $x^{\prime },$ forcément impaire, de

$x{\text{'}}^2-a\equiv 0mod{2}^{n-1}$,

et c'est a plus forte raison une solution modulo $m_1$. On a d'autre part, avec les notations du lemme,

$Q(x^{″})=2^{n-2}{x}^{\prime }{\text{'}}^2+2x^{\prime }{x}^{″}+\frac{x{\text{'}}^2-a}{2^{n-2}}\equiv 2x^{\prime }{x}^{″}+\frac{x{\text{'}}^2-a}{2^{n-2}}mod4\equiv 0⟺x^{\prime }{x}^{″}+\frac{x{\text{'}}^2-a}{2^{n-1}}\equiv 0mod2.$

Et comme $x^{\prime }$ est impair, on a bien une solution $x^{″}$ modulo $m_2$ qui permet de conclure.

• Soit p un nombre premier impair, $a\in \mathbb{Z}$ un nombre premier avec p, n un entier positif, et $f$ une forme quadratique entière d'une ou plusieurs variables: sous forme matricielle, $f(𝐱)=\frac{1}{2}{𝐱}^{T}M𝐱.$ On suppose $\det (M)\equiv ̸0modp$. Alors la congruence $f(𝐱)\equiv amod{p}^n$ est solvable si (et seulement si) la congruence $f(𝐱)\equiv amodp$ l'est.

On prend $P(𝐱)=\frac{1}{2}{𝐱}^{T}M𝐱-a$, et la séparation $m_1=p^n$, $m_2=p$. Supposons le résultat vrai pour n = N.

L'hypothèse d'induction fournit une solution ${𝐱}^{\prime },$ forcément non nulle, de $P({𝐱}^{\prime })\equiv 0mod{p}^n,$ et on a, avec les notations du lemme,

$Q({𝐱}^{″})=\frac{P({𝐱}^{\prime })}{p^n}+𝐱{\text{'}}^{T}M{𝐱}^{″}+\frac{1}{2}{p}^n{𝐱}^{\prime }{\text{'}}^{T}M{𝐱}^{″}\equiv 0modp,\text{ou bien}𝐱{\text{'}}^{T}M{𝐱}^{″}\equiv -\frac{P({𝐱}^{\prime })}{p^n}modp.$

Cette dernière congruence, linéaire en ${𝐱}^{″},$ aura une solution si ${{𝐱}^{\prime }}^{T}M\equiv ̸0$ modulo p. Mais cela a lieu puisque ${𝐱}^{\prime }\equiv ̸0$ et que M est inversible modulo p. Donc la congruence proposée a une solution modulo $p^{n+1}$, et pour tous les moduli $p^k$ en général.

Observons encore que le théorème des restes chinois peut être vu comme un corollaire de ce lemme, en réduisant la question par induction au cas de deux facteurs $m_1:=n_1$ et $m_2:=n_2$, et en appliquant la méthode précédente au polynôme $P(X)=n_2(X-a_1)+n_1(X-a_2)$ (avec les notations du début de l'article).

Utilisations

Le théorème des restes chinois est largement utilisé en arithmétique et en algèbre, notamment sous sa forme générale dans l'arithmétique des corps, que ce soit au cours de démonstrations théoriques aussi bien que dans des cas pratiques.

Dans le domaine de l'algorithmique, il est par exemple utilisé dans l'algorithme RSA en cryptographie, et il intervient aussi dans l'algorithme de Silver-Pohlig-Hellman pour le calcul du logarithme discret. Il intervient dans l'algorithme de test de primalité de Agrawal et Biswas, développé en 1999.

Il permet de représenter de grands nombres entiers comme n-uplets de restes de divisions euclidiennes. Sous cette forme, des opérations comme l'addition ou la multiplication peuvent se faire en parallèle en temps constant (pas de propagation de retenue). Par contre, la comparaison ou la division ne sont pas triviales.

Suite

De façon triviale, voici la suite des 1000 premières itérations répondant à l'énoncé d'origine dit des « restes chinois » (différence de 105 entre deux termes):

23, 128, 233, 338, 443, 548, 653, 758, 863, 968

La suite relative aux pirates, pour les 5000 premières itérations, donne (différence de 1122 entre deux termes) :

785, 1907, 3029, 4151.

Voir aussi

Articles connexes

• Théorème de Bachet-Bézout
• Système couvrant

Bibliographie

• Modèle:Ouvrage

• Modèle:Ouvrage

Liens externes

• Modèle:En Modèle:Langue sur cut-the-knot