Module injectif

En mathématiques, et plus spécifiquement en algèbre homologique, un module injectif est un module Q (à gauche par exemple) sur un anneau A tel que pour tout morphisme injectif f : X → Y entre deux A-modules (à gauche) et pour tout morphisme g : X → Q, il existe un morphisme h : Y → Q tel que hf = g, c'est-à-dire tel que le diagramme suivant commute :

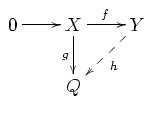
Autrement dit : Q est injectif si pour tout module Y, tout morphisme d'un sous-module de Y vers Q s'étend à Y.

Définitions équivalentes

Les A-modules injectifs sont les Modèle:Lien de la catégorie abélienne des A-modules (lesquels sont les objets projectifs de la catégorie opposée). Par conséquent, on a le

On en déduit qu'un produit de modules est injectif si, et seulement si chaque facteur du produit est injectif.

Une autre caractérisation est :

Modèle:Théorème En effet, si Q est un sous-module injectif d'un module Y alors le morphisme identité de Q sur lui-même peut se prolonger en un morphisme de Y sur Q, ce qui équivaut à dire que Q est facteur direct dans Y. La réciproque vient du fait que pour tout sous-module X d'un module Y, un morphisme de X dans Q s'étend toujours en un morphisme de Y dans la somme amalgamée Z de Q et Y sur X donc aussi, si le sous-module Q de Z est facteur direct, en un morphisme de Y dans Q.

Exemples

ℚ est un ℤ-module injectif, autrement dit un groupe abélien divisible.

Plus généralement, si A est un anneau intègre :

• tout A-module injectif Q est divisible ;
• la réciproque est vraie si A est un anneau de Dedekind ou si Q est sans torsion ;
• le plus petit A-module injectif contenant A est son corps des fractions.

Critère de Baer

Le critère de Baer est l'un des principaux moyens pour établir qu'un module est injectif :

La condition nécessaire est évidente, la condition suffisante s'établit grâce au lemme de Zorn.

On montre à partir du critère de Baer le résultat suivant : si l'anneau A est noethérien à gauche, tout module somme directe de A-modules injectifs est injectif. Réciproquement, si tout module somme directe de A-modules à gauche injectifs est injectif, alors A est noethérien à gauche.

Enveloppe injective

Soit M un A-module à gauche.

Exemple : Soit A un anneau principal, p un élément extrémal de A et $A(p^i)=A/A{p}^i(i\ge 1)$. Soit alors $A\left(p^{\mathrm{\infty }}\right)=\lim {\mathrm{\backslash limits}}_{⟶}A\left(p^i\right)=\bigcup _{i\ge 1}A\left(p^i\right)$. Le module $A\left(p^{\mathrm{\infty }}\right)$ est enveloppe injective de $A(p^i)$ pour tout $i\ge 1$.

Cogénérateurs injectifs

Soit C une catégorie admettant des produits quelconques (ce qui est le cas des A-modules à gauche). Un objet Q est cogénérateur dans C si, et seulement si pour tout objet M de C il existe un ensemble I et un monomorphisme $M\to Q^I$.

Soit $(S_i{)}_{i\in I}$ un système représentatif de A-modules à gauche simples (c'est-à-dire une famille non vide de modules simples tels que $S_i\ne S_j$ si $i\ne j$ et pour tout module simple S il existe un indice $i\in I$ est un isomorphisme $S\to S_i$). Il découle de ce qui précède que le A-module à gauche $Q_0=\underset{i\in I}{⨁}E\left(S_i\right)$ est un cogénérateur, appelé cogénérateur canonique, et il est injectif si A est noethérien à gauche. Un A-module à gauche Q est cogénérateur si, et seulement si, il existe un monomorphisme $Q_0\to Q$. Ceci implique qu'il existe dans la catégorie des A-modules à gauche un cogénérateur, dont l'enveloppe injective est un cogénérateur injectif.

Exemple : Soit A un anneau principal. Tout module simple S est de la forme $A(p)$ où p est un élément extrémal. Puisque l'enveloppe injective de $A(p)$ est $A\left(p^{\mathrm{\infty }}\right)$ (voir supra), $Q_0=\underset{p\in P}{⨁}A\left(p^{\mathrm{\infty }}\right)$, où P est un système représentatif d'éléments extrémaux de A, est le cogénérateur canonique (unique à un isomorphisme près), et il est injectif.

En particulier, supposons que A soit l'anneau des opérateurs différentiels $ℂ\left[\partial \right]$ où $\partial =d/dx$. Un système représentatif d'éléments extrémaux de A est formé des $p_{\zeta }(\partial )=\partial -\zeta ,\zeta \in ℂ$. Soit $C_{n,\zeta }$ le $ℂ$-espace vectoriel engendré par les n fonctions $x\mapsto x^{k-1}{e}^{x\zeta }(1\le k\le n)$ et $\psi :A\to C_{n,\zeta }:r(\partial )\mapsto r(\partial )x^{k-1}{e}^{x\zeta }$. Alors $\psi$ est un épimorphisme de noyau $(p_{\zeta }^n)$, qui induit donc un isomorphisme $A(p_{\zeta }^n)\to C_{n,\zeta }$. Par suite, il existe un isomorphisme

$Q_0\to \underset{\zeta \in ℂ}{⨁}ℂ\left[x\right]e^{x\zeta }$,

autrement dit le cogénérateur canonique est, à un isomorphisme près, l'espace des combinaisons linéaires d'exponentielles-polynômes (pour une généralisation, voir l'article Principe fondamental d'Ehrenpreis).

Il résulte des définitions qu'un A-module à gauche Q est cogénérateur injectif si, et seulement si le foncteur ${\mathrm{H}\mathrm{o}\mathrm{m}}_A(-,Q)$ (de la catégorie des Q-modules à gauche dans celle des groupes abéliens) est fidèle et exact (ceci reste valide si l'on remplace la catégorie des A-modules à gauche par une catégorie abélienne admettant des produits quelconques). Explicitons ce résultat :

Application aux systèmes d'équations linéaires

Les résultats de cette section, essentiellement dus à Oberst, ont fait récemment l'objet d'une présentation systématique un peu plus générale, reprise ci-dessous dans les grandes lignes.

Noyau et conoyau

Soit A un anneau et $R\in A^{n\times m}$. Soit $\bullet R:A^{1\times n}\to A^{1\times m}$ la multiplication à droite par R, ${\mathrm{c}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{r}}_A(\bullet R)=A^{1\times m}/{\mathrm{i}\mathrm{m}}_A(\bullet R)$ son conoyau et Q un A-module à gauche.

(a) Le groupe abélien ${\mathrm{H}\mathrm{o}\mathrm{m}}_A(A^{1\times n},Q)$ s'identifie à $Q^n$ de la manière suivante : soit $({ϵ}_i{)}_{1\le i\le n}$ la base canonique de $A^{1\times n}$, et pour tout $q\in Q^n$ soit ${ℐ}_q\in {\mathrm{H}\mathrm{o}\mathrm{m}}_A(A^{1\times n},Q):{ϵ}_i\mapsto q_i(1\le i\le n)$. Alors $ℐ:q\mapsto {ℐ}_q$ est un isomorphisme canonique de $Q^n$ sur ${\mathrm{H}\mathrm{o}\mathrm{m}}_A(A^{1\times n},Q)$.

(b) Par suite, ${\mathrm{H}\mathrm{o}\mathrm{m}}_A({\mathrm{c}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{r}}_A(\bullet R),Q)$ s'identifie aux éléments de $Q^m$ qui s'annulent sur ${\mathrm{i}\mathrm{m}}_A(\bullet R)$, donc à

${\mathrm{k}\mathrm{e}\mathrm{r}}_Q(R\bullet )=\{q\in Q^m:Rq=0\}$.

Systèmes d'équations linéaires non homogènes

Supposons A noethérien à gauche et soit $R_1\in A^{n_1\times m_1}$. Puisque ${\mathrm{k}\mathrm{e}\mathrm{r}}_A(\bullet R_1)$ est de type fini, il existe un entier $n_2$ et une matrice $R_2\in A^{n_2\times n_1}$, dont les lignes en forment un ensemble générateur, et pour lesquels la suite ci-dessous est donc exacte :

$A^{1\times n_2}\stackrel{\bullet R_2}{⟶}{A}^{1\times n_1}\stackrel{\bullet R_1}{⟶}{A}^{1\times m_1}$.

Considérons maintenant le système d'inconnue $q\in Q^{m_1}$ :

$R_{1}q=f,f\in Q^{n_1}$.

Puisque $R_2{R}_1=0$, ce système linéaire ne peut avoir de solution que si la condition de compatibilité $R_{2}f=0$ est satisfaite. Or, l'exactitude de la seconde suite exacte ci-dessus signifie que ${\mathrm{i}\mathrm{m}}_Q(R_1\bullet )={\mathrm{k}\mathrm{e}\mathrm{r}}_Q(R_2\bullet )$, donc que si $R_{2}f=0$, alors il existe $q\in Q^{m_1}$ tel que $R_{1}q=f$. Par conséquent, si le module Q est injectif, la condition de compatibilité (qui est toujours nécessaire) est suffisante pour que le système linéaire non homogène ait une solution. De plus, pour que cela ait lieu pour tout système linéaire non homogène vérifiant la condition de compatibilité, il faut et il suffit que Q soit injectif.

Systèmes linéaires et modules cogénérateurs

Soit M un A-module à gauche de présentation finie et Q un A-module à gauche. Posons

$M={\mathrm{c}\mathrm{o}\mathrm{k}\mathrm{e}\mathrm{r}}_A(\bullet R)=A^{1\times m}/N,N={\mathrm{i}\mathrm{m}}_A(\bullet R)\subset A^{1\times m},R\in A^{n\times m}$.

Posons d'autre part

${𝔅}_Q=N^{\perp }=\{q\in Q^m:Nq=0\}={\ker }_Q(R\bullet )$,

${𝔅}_Q^{\perp }=\{r\in A^{1\times m}:r{𝔅}_Q=0\}$.

En désignant par ${𝒮}_m$ l'ensemble des sous-modules de type fini de $A^{1\times m}$, la correspondance

${𝒮}_m\leftrightarrow {𝒮}_m^{\perp }:N\mapsto N^{\mathrm{\perp }},{𝔅}_Q\mapsto {𝔅}_Q^{\perp }$

est une connexion de Galois, à savoir que

$N\subset N^{\perp \perp },{𝔅}_Q\subset {𝔅}_Q^{\perp \perp },N^{\perp }=N^{\perp \perp \perp },{𝔅}_Q^{\perp }={𝔅}_Q^{\perp \perp \perp }$.

Notes et références

Références

• Modèle:Ouvrage
• Modèle:Ouvrage
• Modèle:Ouvrage
• Modèle:Ouvrage
• Modèle:Article
• Modèle:Ouvrage

Articles connexes

• Module projectif
• Principe fondamental d'Ehrenpreis