Ajustement de courbe

Ajustement par itérations d'une courbe bruitée par un modèle de pic asymétrique (méthode de Gauss-Newton avec facteur d'amortissement variable).

L'ajustement de courbe est une technique d'analyse d'une courbe expérimentale, consistant à construire une courbe à partir de fonctions mathématiques et d'ajuster les paramètres de ces fonctions pour se rapprocher de la courbe mesurée Modèle:Incise. On utilise souvent le terme anglais Modèle:Lang, Modèle:Lang ou simplement Modèle:Lang, pour désigner cette méthode ; on utilise souvent le franglais « fitter une courbe » pour dire « ajuster une courbe ».

On utilise des méthodes de régression. Dans les cas simples, il s'agit de régression multilinéaire si la loi est linéaire pour tous les paramètres, ou de régression polynomiale lorsque l'on utilise un polynôme pour simuler le phénomène (les paramètres physiques pouvant être déduits des coefficients du polynôme).

Les méthodes de régression classiques permettent de déterminer les paramètres à partir de calculs sur les données, mais sont inapplicables si la fonction est trop complexe. Il faut alors travailler par essai-erreur pour se rapprocher d'une solution, au sens de la méthode des moindres carrés. La solution n'est pas nécessairement unique.

Ajustement algébrique ou géométrique

On distingue deux types d'ajustement :

• les ajustements algébriques consistent à minimiser l'écart vertical (en y) entre la courbe modèle et les points expérimentaux ;
• les ajustements géométriques consistent à minimiser la distance perpendiculairement à la courbe modèle ; c'est le cas par exemple de la régression circulaire ou elliptique, qui consiste à trouver le cercle, resp. l'ellipse, la plus proche des points

Dans le cas d'un ajustement géométrique, on parle de la méthode des moindres carrés totaux (Modèle:Lang, TLS) : en effet, on prend en compte les deux coordonnées x et y pour la détermination de l'écart quadratique.

Fonction modèle utilisée

Régression sur un nuage de points par un polynôme de degré croissant.

Dans certains cas, on a un modèle théorique permettant de prévoir la forme de la courbe ; la méthode d'ajustement permet de déterminer les paramètres de l'échantillon. Dans d'autres cas, on utilise une fonction empirique ; on s'intéresse alors en général à la surface, la largeur ou à la position du maximum de la fonction.

On utilise souvent des polynômes : ce sont des modèles qui se calculent facilement. Pour les formes de type « pic » (distributions unimodales), on utilise fréquemment des fonctions gaussiennes, lorentziennes ou bien des combinaisons (fonctions ou pseudo-fonctions de Voigt), ou encore des fonctions de Pearson. Les courbes présentant un amortissement comportent fréquemment une composante exponentielle négative (fonction en Modèle:Math) ; les courbes en S peuvent être modélisées par une fonction sigmoïde.

De manière générale, on a une fonction Modèle:Mvar modèle ayant Modèle:Mvar paramètres Modèle:Math qui relie l'abscisse Modèle:Mvar à l'ordonnée Modèle:Mvar :

$y=f(p^1,p^2,\dots ,p^n,x)$

et on compare cette fonction avec les Modèle:Mvar points expérimentaux

$[(x_1,y_1^{\text{exp}}),(x_1,y_1^{\text{exp}}),\dots ,(x_m,y_m^{\text{exp}})].$

La fonction Modèle:Mvar peut être parfois décomposée en plusieurs fonctions Modèle:Math soit qu'elle en est la somme, le produit, le produit de convolution…

$f=f_1+f_2+\dots \text{ ou }f=f_1\times f_2\times \dots \text{ ou }f=f_1*f_2*\dots$

Démarche de régression

Considérations générales

On calcule les points Modèle:Math de la courbe simulée :

$y_i^{\text{cal}}=f\left(x_i\right)$.

Habituellement, on utilise un algorithme de régression visant à minimiser l'écart quadratique entre la courbe simulée et la courbe expérimentale ; on parle d'algorithme de minimisation de l'erreur.

On définit donc un facteur de fiabilité (Modèle:Lang) Modèle:Math :

$\mathrm{R}=\sqrt{\frac{\sum _i{(y_i^{\mathrm{e}\mathrm{x}\mathrm{p}}-y_i^{\mathrm{c}\mathrm{a}\mathrm{l}})}^2}{\sum _i{y_i^{\mathrm{e}\mathrm{x}\mathrm{p}}}^2}}$

où Modèle:Math est le Modèle:Mvar-ème point mesuré et Modèle:Math est le Modèle:Mvar-ème point calculé. Le facteur Modèle:Math est similaire dans son expression au coefficient de corrélation multiple (Modèle:Math étant alors le coefficient de détermination). On utilise plus couramment le facteur de fiabilité pondérée (Modèle:Lang) Modèle:Math :

${\mathrm{R}}_{\mathrm{w}\mathrm{p}}=\sqrt{\frac{\sum _i{w}_i\cdot {(y_i^{\mathrm{e}\mathrm{x}\mathrm{p}}-y_i^{\mathrm{c}\mathrm{a}\mathrm{l}})}^2}{\sum _i{w}_i\cdot {y_i^{\mathrm{e}\mathrm{x}\mathrm{p}}}^2}}$

où Modèle:Mvar est le poids attribué au point Modèle:Mvar ; ce poids représente l'incertitude associée au point Modèle:Mvar.

La régression consiste à trouver le jeu de paramètres Modèle:Math tel que Modèle:Math est minimal. On a donc notamment

$\mathrm{\forall }i,\frac{\partial {\mathrm{R}}_{\mathrm{w}\mathrm{p}}}{\partial p^i}=0$.

Dans les cas simples, le système d'équations que l'on obtient peut se résoudre « simplement » ; en particulier pour les régressions multilinéaires, on peut le résoudre par inversion de matrice.

Régression non linéaire

Lorsqu'il n'est pas possible de résoudre simplement le système d'équations, on peut utiliser la méthode de Newton-Raphson.

C'est un algorithme itératif : à chaque étape, on regarde de quelle manière une petite variation d'un paramètre fait varier la fonction de fiabilité Modèle:Math. Le jeu de paramètre retenu pour l'étape suivante est obtenue par extrapolation de ces petites variations, par linéarisation : on cherche les valeurs des paramètres qui rendraient Modèle:Math nul si les variations de Modèle:Math étaient proportionnelles aux variations des paramètres. Le calcul s'arrête lorsque l'on n'arrive plus à diminuer le facteur de fiabilité, on parle de convergence.

Si l'on note Modèle:Math l'ensemble des paramètres, l'intensité calculée en chaque point Modèle:Mvar à l'étape Modèle:Mvar s'exprime par

$y_i^{\mathrm{c}\mathrm{a}\mathrm{l}}=f(p_j^1,p_j^2,\dots ,p_j^n,x_i)$.

Pour simplifier les calculs, on peut faire un développement limité du premier ordre de cette fonction $f$, alors en appliquant des incréments Modèle:Math aux paramètres, on peut écrire :

$f(p_j^1+\mathrm{\Delta }{p}_j^1,\dots ,p_j^n+\mathrm{\Delta }{p}^n,x_i)\simeq f(p_j^1,\dots ,p_j^n,x_i)+\sum _k\frac{\partial f}{\partial p^k}\left(x_i\right)\cdot \mathrm{\Delta }{p}^k$

en imposant Modèle:Math, on obtient ainsi un système d'équations linéaires (l'indice Modèle:Mvar est omis pour plus de clarté) :

$\left(\begin{array}{cccc}\frac{\partial f}{\partial p^1}(x_1)& \frac{\partial f}{\partial p^2}(x_1)& \cdots & \frac{\partial f}{\partial p^n}(x_1)\\ \frac{\partial f}{\partial p^1}(x_2)& \frac{\partial f}{\partial p^2}(x_2)& \cdots & \frac{\partial f}{\partial p^n}(x_2)\\ ⋮& ⋮& & ⋮\\ \frac{\partial f}{\partial p^1}(x_m)& \frac{\partial f}{\partial p^2}(x_m)& \cdots & \frac{\partial f}{\partial p^n}(x_m)\end{array}\right)\left(\begin{array}{c}\mathrm{\Delta }{p}^1\\ \mathrm{\Delta }{p}^2\\ ⋮\\ \mathrm{\Delta }{p}^n\end{array}\right)+\left(\begin{array}{c}f(p^1,\dots ,p^n,x_1)\\ f(p^1,\dots ,p^n,x_2)\\ ⋮\\ f(p^1,\dots ,p^n,x_m)\end{array}\right)=\left(\begin{array}{c}{y}_1^{\mathrm{e}\mathrm{x}\mathrm{p}}\\ y_2^{\mathrm{e}\mathrm{x}\mathrm{p}}\\ ⋮\\ y_m^{\mathrm{e}\mathrm{x}\mathrm{p}}\end{array}\right)$

qui peut se résoudre par une pseudo-inversion de matrice, ce qui permet de calculer les Modèle:Math et donc les valeurs des paramètres à l'étape suivante Modèle:Mvar :

si l'on appelle Modèle:Mvar la matrice ${(\frac{\partial f}{\partial p^k}(x_i))}_{i,k}$, le système d'équations s'écrit :

$A{\left(\mathrm{\Delta }{p}_j^k\right)}_k+{\left(y_i^{\text{cal}}\right)}_i={\left(y_i^{\text{exp}}\right)}_i$

La matrice pseudo-inverse Modèle:Mvar a les mêmes dimensions que Modèle:Math (la matrice transposée de Modèle:Mvar) et vérifie :

• Modèle:Math ;
• Modèle:Math ;
• Modèle:Math et Modèle:Math sont hermitiennes.

La matrice pseudo-inverse peut se calculer par décomposition en valeurs singulières.

On prend alors

${\left(\mathrm{\Delta }{p}_j^k\right)}_k=B[{\left(y_i^{\text{exp}}\right)}_i-{\left(y_i^{\text{cal}}\right)}_i]$

et

${\left(p_{j+1}^k\right)}_k={\left(p_j^k\right)}_k+{\left(\mathrm{\Delta }{p}_j^k\right)}_k$.

La pseudo-inversion est justifiée par le fait que le premier membre du système d'équations s'écrit alors :

$A\times {\left(\mathrm{\Delta }{p}_j^k\right)}_k=A\times B\times [{\left(y_i^{\text{exp}}\right)}_i-{\left(y_i^{\text{cal}}\right)}_i]$ ;

si on le multiplie par B, il devient :

$B\times A\times B\times [{\left(y_i^{\text{exp}}\right)}_i+{\left(y_i^{\text{cal}}\right)}_i]=B\times {\left(y_i^{\text{exp}}\right)}_i+B\times {\left(y_i^{\text{cal}}\right)}_i$

et donc on a bien

$B\times [A\times {\left(\mathrm{\Delta }{p}_j^k\right)}_k-{\left(y_i^{\text{cal}}\right)}_i]=B\times {\left(y_i^{\text{exp}}\right)}_i$.

Notons qu'il s'agit d'une condition suffisante, mais pas nécessaire.

Il s'agit bien d'une méthode de Newton-Raphson, puisque l'on linéarise la fonction et que l'on cherche le point qui annule Modèle:Math (Modèle:Math si Modèle:Math pour tout Modèle:Mvar).

En remarquant que Modèle:Mvar est en fait la matrice jacobienne de $f$ (Modèle:Math), on voit que le système d'équations est constitué des équations normales. Les incréments des paramètres peuvent alors se calculer par :

${\left(\mathrm{\Delta }{p}^k\right)}_k=-{({}^{\text{t}}J\times J)}^{-1}\times {}^{\text{t}}J\times [{\left(y_i^{\text{exp}}\right)}_i-{\left(y_i^{\text{cal}}\right)}_i]$.

On retrouve alors l'algorithme de Gauss-Newton.

Parfois, la linéarisation est « trop violente » : si la fonction présente une « courbure » importante lorsque les paramètres varient, l'application de la « loi tangente » peut éloigner de la solution plutôt que rapprocher. On peut donc utiliser un coefficient d'atténuation Modèle:Math, on a alors :

${\left(p_{j+1}^k\right)}_k={\left(p_j^k\right)}_k+d\cdot {\left(\mathrm{\Delta }{p}_j^k\right)}_k$.

On peut aussi utiliser un algorithme plus complexe utilisant les dérivées secondes.

Il peut arriver que le programme converge vers un minimum local de Modèle:Math qui n'est pas le minimum absolu. Pour éviter cette situation, on utilise l'algorithme de Metropolis-Hastings : lorsque l'on a convergé, on fait varier les paramètres d'une certaine valeur et on recommence le processus pour voir si l'on arrive à converger vers un autre jeu de paramètres ayant un facteur de fiabilité plus faible.

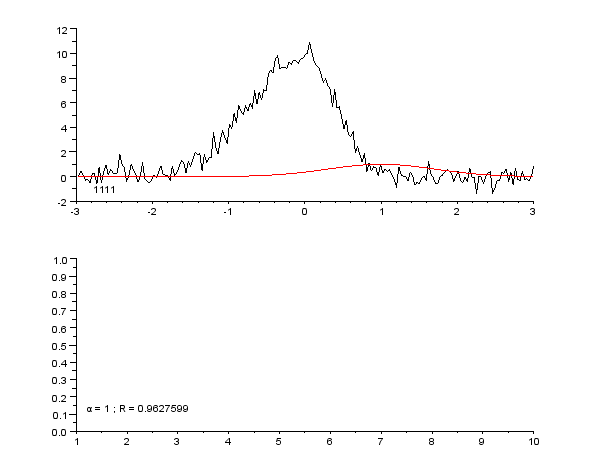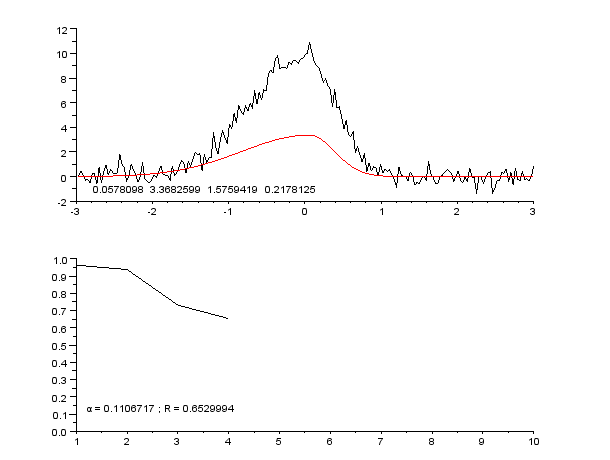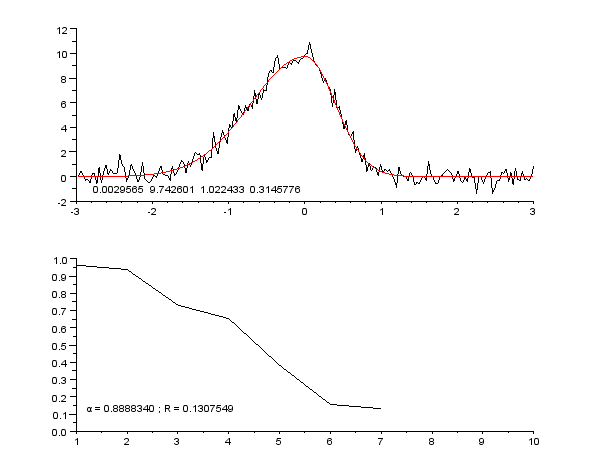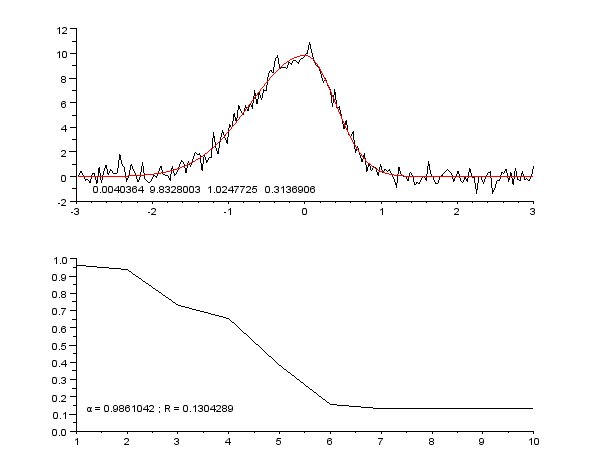
Si la simulation était parfaite, le facteur de fiabilité aurait une valeur dépendant du rapport signal sur bruit. Si l'on sait calculer ce rapport signal sur bruit, c'est-à-dire si l'on connaît la loi de probabilité régissant les fluctuations du signal, on peut alors déterminer un facteur de fiabilité incompressible Modèle:Math. Si la simulation est parfaite, on a alors Modèle:Math de fait, la qualité de la simulation est souvent exprimée par le rapport Modèle:Math, qui doit tendre vers 1 au fur et à mesure des étapes itératives.

Régression circulaire

Modèle:Article détaillé La régression circulaire consiste à trouver le « meilleur cercle », au sens des moindres carrés, décrivant un ensemble de points. C'est un problème de régression géométrique non linéaire. Cependant, un choix astucieux de la fonction d'erreur permet de se ramener à un problème linéaire.

Régression elliptique

Régression elliptique.

La régression elliptique consiste à trouver la « meilleure ellipse », au sens des moindres carrés, décrivant un ensemble de points.

Applications

• Déconvolution
• Méthode de Rietveld
• Compression de courbe

Voir aussi

Articles connexes

• Approximation de fonction
• Interpolation (mathématiques)
• Régression multilinéaire
• Algorithme de Levenberg-Marquardt