Constante de connectivité

En mathématiques, la constante de connectivité est une constante associée aux chemins auto-évitants d'un réseau. Elle est étudiée en relation avec la notion d'universalité dans les modèles de physique statistique. Bien que les constantes de connectivités dépendent du choix du réseau (à l'instar d'autres quantités telles que le seuil critique de probabilité de percolation), elles apparaissent néanmoins dans des conjectures de lois universelles. En outre, les techniques mathématiques utilisées pour les comprendre, par exemple, dans la récente preuve rigoureuse par Duminil-Copin et Smirnov de la valeur exacte de cette constante pour le réseau hexagonal, peuvent fournir des pistes pour attaquer d'autres problèmes importants, notamment la conjecture que les chemins auto-évitants convergent dans la limite d'échelle vers l'Modèle:Lien.

Définition

Soit $c_n$ le nombre de chemins auto-évitants de longueur $n$ partant d'un point donné du réseau (graphe infini sommets-transitif). Comme un chemin auto-évitant de longueur $n+m$ peut être décomposé en deux chemins auto-évitants de longueur $n$ et $m$, il s'ensuit que $c_{n+m}⩽c_n{c}_m$. Puis, en appliquant le lemme sous-additif au logarithme de $c_n$, on obtient l'existence de

$\mu =\underset{n\to \mathrm{\infty }}{\lim }{c}_n^{1/n}$.

Ce nombre est appelé la constante de connectivité du réseau. Sa valeur exacte n'est connue que pour deux réseaux classiques, voir ci-dessous. Pour les autres réseaux, $\mu$ a seulement été approchée numériquement en utilisant la conjecture $\frac{c_{n+1}}{c_n}\to \mu$, à propos de laquelle il a seulement été démontré que $\frac{c_{n+2}}{c_n}\to {\mu }^2$.

Il est de plus conjecturé que

$c_n\sim c{\mu }^n{n}^{\gamma }$

lorsque n tend vers l'infini, où $\mu$ dépend du réseau mais l'exposant $\gamma$ est universel (il dépend de la dimension, mais pas du réseau). En dimension deux, il est conjecturé que $\gamma =11/32$Modèle:,. On approche $\gamma$ numériquement en utilisant $\frac{c_{n-1}{c}_{n+1}}{c_n^2}\simeq 1-\frac{\gamma }{n^2}$.

Valeurs connues

Ces valeurs données ci-dessous sont tirées de l'article d'Iwan Jensen et Anthony Guttmann.

Type du réseau	Description (code-sommet pour un pavage semi-régulier)	Constante de connectivité	Référence OEIS pour la suite des décimales
hexagonal	$6^3$ (i.e. 3 hexagones par nœud)	$=\sqrt{2+\sqrt{2}}=2\cos \frac{\pi }{8}=1,847759...$	Modèle:OEIS
triangulaire	$3^6$	$\approx 4,15079$
carré ${\mathbb{Z}}^2$	$4^4$	$\approx 2,63815853$	cf. Modèle:OEIS : valeur coïncidant sur 8 décimales
échelle $\mathbb{Z}\times \{0,1\}$	Deux droites reliées par des barreaux	$=\frac{1+\sqrt{5}}{2}=1,6180339...$ (nombre d'or)	La suite $(c_n)$ est référencée comme Modèle:OEIS .
carré Manhattan-orienté		$\approx 1,733535$
carré orienté en L		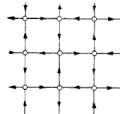$\approx 1,5657$
trihexagonal	$(3\cdot 6{)}^2$	$\approx 2,56062$
hexagonal tronqué	$3\cdot 12^2$	$=1,7110412...$	Modèle:OEIS
carré tronqué	$4\cdot 8^2$	$\approx 1,80883001$
cubique ${\mathbb{Z}}^3$		$\approx 4,755995$
hypercubique ${\mathbb{Z}}^d$		$\in [d,2d-1]$

Comme chaque pas dans le réseau hexagonal correspond à deux ou trois pas pour le réseau hexagonal tronqué, la constante de connectivité de ce dernier réseau peut être exprimée exactement ; c'est la plus grande racine réelle du polynôme $x^{12}-4x^8-8x^7-4x^6+2x^4+8x^3+12x^2+8x+2$.

Plus d'informations sur ces réseaux peuvent être trouvées dans l'article sur le Modèle:Lien.

Preuve de Duminil-Copin–Smirnov

En 2010, Hugo Duminil-Copin et Stanislav Smirnov ont publié la première preuve rigoureuse du fait que $\mu =\sqrt{2+\sqrt{2}}=2\cos \frac{\pi }{8}$ pour le réseau hexagonal.

Cela avait été conjecturé par Nienhuis en 1982 dans le cadre d'une étude plus large de modèles en $O(n)$ à l'aide de techniques de renormalisation. Cette preuve est issue d'un programme consistant à appliquer des outils d'analyse complexe à des modèles probabilistes, programme qui a également produit des résultats impressionnants pour le modèle d'Ising, entre autres.

L'argument repose sur l'existence d'une "observable parafermionique" qui satisfait la moitié des équations discrètes de Cauchy–Riemann pour le réseau hexagonal.

Nous allons modifier légèrement la définition d'un chemin auto-évitant en le faisant commencer et terminer au milieu d'une arête. Soit H l'ensemble de tous les milieux des arêtes du réseau hexagonal supposé plongé dans le plan complexe. Pour un chemin auto-évitant $\gamma$ entre les deux milieux d'arêtes a et b , nous appelons $\ell (\gamma )$ le nombre de sommets visités et $W_{\gamma }(a,b)$son nombre d'enroulement ou "winding" égal à la totalité de la rotation de la direction en radians quand on parcourt $\gamma$ de a à b . Le but de la démonstration est de prouver que la fonction "de partition" $Z(x)=\sum _{\gamma :a\to H}{x}^{\ell (\gamma )}=\sum _{n=0}^{\mathrm{\infty }}{c}_n{x}^n$a un rayon de convergence égal à $x_c=1/\sqrt{2+\sqrt{2}}$. Cela implique en effet immédiatement que $\mu =\underset{n\to \mathrm{\infty }}{\lim }{c}_n^{1/n}=\sqrt{2+\sqrt{2}}$.

Étant donné un domaine $\mathrm{\Omega }$ dans le réseau hexagonal, un milieu d'arête a et deux paramètres x et $\sigma$, nous définissons "l'observable parafermionique"

$F(z)=\sum _{\gamma \subset \mathrm{\Omega }:a\to z}{e}^{-i\sigma W_{\gamma }(a,z)}{x}^{\ell (\gamma )}$.

Si $x=1/\sqrt{2+\sqrt{2}}$ et $\sigma =5/8$, alors pour tout sommet s de $\mathrm{\Omega }$ nous avons $(p-s)F(p)+(q-s)F(q)+(r-s)F(r)=0$ où p,q,r sont les milieux des arêtes émanant de s. Ce lemme établit que l'observable parafermionique est de divergence nulle. Il n'a pas été montré que son rotationnel est nul mais cela permettrait de résoudre plusieurs problèmes ouverts (voir les conjectures). La preuve de ce lemme est un savant calcul qui dépend fortement de la géométrie du réseau hexagonal.Ensuite, nous nous concentrons sur un domaine trapézoïdal $S_{T,L}$ avec 2L cellules formant le côté gauche, T cellules au travers, et des côtés supérieur et inférieur avec un angle de $\pm \pi /3$ (image nécessaire).

Nous avons intégré le réseau hexagonal dans le plan complexe, de sorte que l'arête de longueur 1 et  la mi-arête dans le centre de la gauche est positionné en −1/2. Puis les sommets sont donnés par $V(S_{T,L})=\{z\in V(ℍ):0\le Re(z)\le \frac{3T+1}{2},|\sqrt{3}Im(z)-Re(z)|\le 3L\}$.

Nous définissons alors les fonctions de partition pour les chemins auto-évitants partant de a et aboutissant à la frontière. Soit $\alpha$ la partie gauche de la frontière, $\beta$ la droite, $ϵ$la partie supérieure, et $\overline{ϵ}$ la partie inférieure. Soit $A_{T,L}^x:=\sum _{\gamma \in S_{T,L}:a\to \alpha \setminus \{a\}}{x}^{\ell (\gamma )},B_{T,L}^x:=\sum _{\gamma \in S_{T,L}:a\to \beta }{x}^{\ell (\gamma )},E_{T,L}^x:=\sum _{\gamma \in S_{T,L}:a\to ϵ\cup \overline{ϵ}}{x}^{\ell (\gamma )}$.

En additionnant l'identité $(p-s)F(p)+(q-s)F(q)+(r-s)F(r)=0$sur tous les sommets de $V(S_{T,L})$ et notant que le "winding" est fixé en fonction de la partie de la frontière où le chemin se termine, nous arrivons à la relation $1=\cos (3\pi /8)A_{T,L}^{x_c}+B_{T,L}^{x_c}+\cos (\pi /4)E_{T,L}^{x_c}$après un autre habile calcul. Faisant $L\to \mathrm{\infty }$, on obtient une bande $S_T$ et les fonctions de partition $A_T^x:=\sum _{\gamma \in S_T:a\to \alpha \setminus \{a\}}{x}^{\ell (\gamma )},B_T^x:=\sum _{\gamma \in S_T:a\to \beta }{x}^{\ell (\gamma )},E_T^x:=\sum _{\gamma \in S_T:a\to ϵ\cup \overline{ϵ}}{x}^{\ell (\gamma )}$.

Il a été montré plus tard que $E_{T,L}^{x_c}=0$ mais nous n'avons pas besoin de cela pour la preuve.

Nous nous retrouvons avec la relation $1=\cos (3\pi /8)A_{T,L}^{x_c}+B_{T,L}^{x_c}$. De là, nous pouvons déduire l'inégalité $A_{T+1}^{x_c}-A_T^{x_c}⩽x_c(B_{T+1}^{x_c}{)}^2$.

Et arriver par induction à une limite inférieure strictement positive pour $B_T^{x_c}$. Puisque $Z(x_c)\ge \sum _{T>0}{B}_T^{x_c}=\mathrm{\infty }$nous avons établi que $\mu \ge \sqrt{2+\sqrt{2}}$.

Pour l'inégalité inverse, pour un chemin auto-évitant arbitraire d'un treillis hexagonal, nous procédons à une décomposition canonique due à Hammersley et Welsh du chemin  dans les ponts de largeurs $T_{-I}<\cdots <T_{-1}$ et $T_0>\cdots >T_j$ . Notez que nous pouvons lier $B_T^x⩽(x/x_c{)}^T{B}_T^{x_c}⩽(x/x_c{)}^T$ce qui implique $\prod _{T>0}(1+B_T^x)<\mathrm{\infty }$.

Enfin, il est possible de lier la fonction de partition aux fonctions de partition de pont : $Z(x)\le \sum _{T_{-I}<\cdots <T_{-1},T_0>\cdots >T_j}2\left(\prod _{k=-I}^j{B}_{T_k}^x\right)=2{(\prod _{T>0}(1+B_T^x))}^2$.

Nous obtenons donc $\mu =\sqrt{2+\sqrt{2}}=2\cos \frac{\pi }{8}$ comme souhaité.

Conjectures

Flory a estimé la distance moyenne de l'extrémité $w_n$ au point de départ O d'un chemin auto-évitant du réseau carré de longueur n : $\sqrt{\frac{1}{c_n}\sum _{\mathrm{C}\mathrm{A}\mathrm{E}\mathrm{d}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{u}\mathrm{e}\mathrm{u}\mathrm{r}n}\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(0,w_n{)}^2}$ à $n^{3/4}$(alors que celle-ci est de $n^{1/2}$pour un chemin quelconque).

L'exposant de mise à l'échelle $3/4$ et la constante universelle $11/32$ pourrait être justifiés si les chemins auto-évitants possédaient un invariant conforme d'échelle limite, conjecturé être une Modèle:Lien avec $\kappa =8/3$.

Voir aussi

• Modèle:Lien.

Liens externes

• Weisstein, Eric W. "Self-avoiding walk connective constant". MathWorld.