Projection stéréographique

Projection stéréographique depuis le pôle sud sur le plan équatorial.

Une autre représentation de la projection stéréographique : on projette à partir du pôle nord sur le plan tangent au pôle sud.

Projection stéréographique de la figure de pôles d'un réseau cristallin de diamant selon l'axe [111] qui montre la symétrie le long de la diagonale d'espace du cube élémentaire.

En géométrie et en cartographie, la projection stéréographique est une projection cartographique azimutale permettant de représenter une sphère privée d'un point sur un plan.

On convient souvent que le point dont on prive la sphère sera un des pôles de celle-ci ; le plan de projection peut être celui qui sépare les deux hémisphères, nord et sud, de la sphère, qu'on appelle plan équatorial. On peut également faire une projection stéréographique sur n'importe quel plan parallèle au plan équatorial pourvu qu'il ne contienne pas le point dont on a privé la sphère.

Soit S le point que l'on retire de la sphère à projeter, considéré par exemple comme son pôle sud. L’image Z’ d’un point Z de cette sphère sera définie par l’intersection entre le plan équatorial et la droite (SZ). (Cette projection revient à observer la sphère à partir du pôle sud).

Deux propriétés importantes :

• tout cercle sur la sphère — hormis ceux passant par le pôle sud — sera transformé en un autre cercle dans le plan équatorial ;
• les angles sont conservés pendant la transformation (transformation conforme).

Remarques :

• l’équateur reste lui-même durant cette transformation ;
• un point de l’hémisphère nord sera projeté à l’intérieur de l’équateur (par exemple dans notre figure, H2 devient H2’ ), un point de l’hémisphère sud à l’extérieur (H1 devient H1’ ) ;
• pour tracer un cercle projeté, il suffit donc de trouver deux points définissant un diamètre ;
• on peut définir de façon analogue une projection à partir du pôle nord, comme le montre la deuxième figure.

La projection stéréographique était utilisée dans la conception des astrolabes arabes de l’époque médiévale. Elle est amplement utilisée en cristallographie pour étudier la symétrie morphologique des cristaux, et notamment pour représenter les formes cristallines, un exemple étant donné à la troisième figure.

Les mathématiques de la projection stéréographique

Aspect géométrique

Projection stéréographique du pôle nord sur un plan non équatorial.

Coupe d'une projection stéréographique par un plan passant par le centre de la sphère, le pôle nord et le point à transformer. Cette fois-ci, le plan de projection n'est pas équatorial.

Une sphère de dimension Modèle:Mvar est l'ensemble des points de l'espace de dimension Modèle:Math situés à distance Modèle:Mvar du centre de la sphère. Si on ne précise pas le type de distance, on utilise la distance euclidienne de deux points, de vecteurs de coordonnées Modèle:Mvar et Modèle:Mvar, distance donnée par la norme euclidienne du vecteur Modèle:Math :

$|v-u|={(\sum _{j=1}^{n+1}|v_j-u_j{|}^2)}^{1/2}$

La projection stéréographique permet de définir un homéomorphisme entre une sphère de dimension Modèle:Mvar privée d'un point et l'espace de dimension Modèle:Mvar. La présentation qui suit est valable en dimension Modèle:Math quelconque, mais le cas particulier d'une sphère ordinaire peut être lu sans autre modification que de remplacer le mot « hyperplan » par le mot « plan » dans ce qui suit.

Géométriquement, notons Modèle:Mvar (comme Nord) le point particulier dont on va priver la sphère. Soit Modèle:Math un hyperplan perpendiculaire au rayon déterminé par Modèle:Mvar. On supposera que cet hyperplan plan n'est pas le plan tangent en Modèle:Mvar à la sphère.

Soit Modèle:Math un point de la sphère. Notons Modèle:Mvar la droite déterminée par Modèle:Mvar et Modèle:Mvar ; cette droite n'est jamais parallèle au plan Modèle:Math, parce que seules les droites tangentes à la sphère en Modèle:Mvar sont parallèles à Modèle:Math. En particulier, Modèle:Mvar n'est pas entièrement contenue dans Modèle:Math. Il y a donc un unique point d'intersection de Modèle:Mvar avec Modèle:Math. Ce point est l'image de Modèle:Mvar par projection stéréographique. Réciproquement, si Modèle:Mvar est un point du plan Modèle:Math, comme ce plan ne passe pas par Modèle:Mvar, la droite déterminée par Modèle:Mvar et Modèle:Mvar coupe la sphère en Modèle:Mvar et en un autre point Modèle:Mvar, qui est l'image réciproque de Modèle:Mvar par projection stéréographique.

Afin de comprendre visuellement ce qui se produit, on remarque que toute la construction se passe dans l'hyperplan de dimension Modèle:Math déterminé par le centre de la sphère, Modèle:Mvar et Modèle:Mvar (ou Modèle:Mvar). On se rapportera à la figure faite en dimension Modèle:Math, dans cet hyperplan (donc un plan, ici) pour bien voir la construction.

Aspect analytique

Du point de vue analytique, on simplifie le calcul en fixant l'origine des coordonnées au centre de la sphère, le pôle nord sur le Modèle:Math-ième axe de coordonnées, et le rayon de la sphère égal à l'unité. Les deux premiers choix sont simplement un choix de repère. Le dernier est un choix d'unité de longueur. Si on désire changer cette dernière, on pourra pratiquer une homothétie sur les formules ci-dessous, afin de traiter le cas d'une sphère de rayon Modèle:Mvar quelconque.

Avec ces choix, la sphère unité Modèle:Mvar de ${ℝ}^{n+1}$ est définie par :

$S^n=\{x=(x_1,\dots ,x_n,x_{n+1}):\sum _{j=1}^{n+1}{\left|x_j\right|}^2=1\}.$

Posons Modèle:Math. Le point Modèle:Mvar a pour coordonnées $y=0\in {ℝ}^n$ et Modèle:Math. L'hyperplan Modèle:Math a pour équation Modèle:Math. Les points de Modèle:Math auront comme coordonnée courante Modèle:Math, avec $\xi \in {ℝ}^n$.

Géométriquement, Modèle:Math et Modèle:Math sont non nuls et colinéaires. Il existe donc un scalaire non nul Modèle:Mvar tel que

$y=\lambda \xi ,s-1=\lambda (h-1).$

Si on se donne Modèle:Math dans Modèle:Mvar, on substitue Modèle:Mvar par Modèle:Mvar et Modèle:Mvar par Modèle:Math dans la relation de définition Modèle:Math. Un bref calcul fournit, après division par Modèle:Math, la relation

$\lambda =\frac{2(1-h)}{|\xi {|}^2+(1-h{)}^2}.$

Le choix Modèle:Math assure que Modèle:Mvar est toujours bien défini. La valeur de Modèle:Mvar et Modèle:Mvar en fonction de Modèle:Mvar est donc

$y=\frac{2(1-h)\xi }{|\xi {|}^2+(1-h{)}^2},s=\frac{|\xi {|}^2-(1-h{)}^2}{|\xi {|}^2+(1-h{)}^2}.$

Réciproquement, si Modèle:Mvar et Modèle:Mvar sont donnés, on aura

$\lambda =\frac{s-1}{h-1},\xi =\frac{(h-1)y}{s-1}.$

L'image par projection stéréographique d'un grand cercle passant par Modèle:Mvar est une droite passant par le point Modèle:Math. L'image d'un cercle quelconque tracé sur la sphère et passant par Modèle:Mvar est la droite formée de l'intersection de Modèle:Math avec le plan déterminé par le cercle. L'image d'un cercle ne passant pas par Modèle:Mvar est un cercle de l'hyperplan Modèle:Math.

Transformation conforme

Démonstration géométrique du fait qu'une projection stéréographique est une transformation conforme.

Une projection stéréographique est une transformation conforme : l'angle entre deux droites tangentes en un même point à la sphère est le même que l'angle entre leur projection. Pour le voir, il suffit de vérifier que la matrice jacobienne de la projection stéréographique est celle d'une similitude.

On peut aussi en donner une démonstration géométrique. Soit M un point de la sphère autre que le pôle nord N et soit deux droites tangentes à la sphère en M. Soient les deux plans passant par N et M, et contenant respectivement chacune des deux droites. Les intersections de ces plans avec le plan de projection sont les images par la projection des deux droites tangentes en M. De plus, ces deux plans découpent dans la sphère deux cercles ayant la corde [NM] en commun et tangents aux deux droites initiales. Considérons les tangentes en N à chacun de ces deux cercles. Elles sont contenues dans chacun des deux plans, et parallèles au plan de projection. Elles sont donc parallèles aux projections des deux droites tangentes en M. L'angle qu'elles forment est donc égal à l'angle entre les deux projections. Mais par ailleurs, du fait de la symétrie des deux cercles par rapport au plan médiateur de [MN], N et les deux tangentes en N sont symétriques de M et des tangentes en M par rapport à ce plan médiateur, donc l'angle entre les tangentes en M est égal à celui entre les tangentes en N. Par conséquent, l'angle entre les deux tangentes en M est le même que celui entre leur projection.

Image des cercles

La projection stéréographique transforme les cercles de la sphère en cercles du plan de projection.

Tout cercle est transformé par la projection stéréographique en un cercle du plan de projection (ou une droite si le pôle N de la projection appartient au cercle à projeter). Si le plan du cercle et le plan de projection sont parallèles, la projection dilate ou contracte le cercle et le translate perpendiculairement aux plans, en le laissant fixe si le plan du cercle est égal au plan de projection.

Pour le cas le plus fréquent où le plan du cercle est distinct du plan de projection, considérons le cône tangent à la sphère le long du cercle (C) à projeter. Soit P son sommet et P' son image par la projection stéréographique. Alors (C) se projettera en un cercle (C') de centre P'. En effet, l'image d'une génératrice quelconque du cône est l'intersection du plan qui la contient et qui passe par N, avec le plan de projection. Il s'agit donc d'une droite passant par P'. Par ailleurs, la génératrice coupe (C) à angle droit et, la projection stéréographique étant conforme, son image coupe (C') également à angle droit. (C') est donc une courbe coupant toute droite issue de P' à angle droit. Il s'agit d'un cercle de centre P'. Modèle:Clr

Généralisation

Cinq exemples de « cercles » unité pour des normes non euclidiennes.

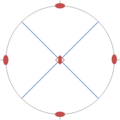
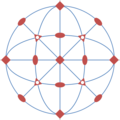
On peut définir la projection stéréographique de n'importe quelle sphère « arrondie » sur un plan : si la boule unité pour une norme de ${ℝ}^{n+1}$ est strictement convexe, c'est-à-dire si le bord de cette boule unité ne contient aucun segment de droite, alors la même construction fonctionne encore, mais le résultat peut dépendre fortement du choix du point Modèle:Mvar, puisqu'une telle sphère n'est isotrope, c'est-à-dire invariante par rotations de l'espace de dimension Modèle:Math, que si elle est euclidienne.

La figure montre quelques « cercles » unité pour la norme

$|x{|}_p={(|x_1{|}^p+|x_2{|}^p)}^{1/p},$

pour Modèle:Mvar strictement compris entre 1 et l'infini. Pour Modèle:Math et pour Modèle:Math, le cercle unité relatif à ces normes n'est pas assez arrondi pour assurer l'unicité de la projection stéréographique, ou son existence. Modèle:Clr

Projection stéréographique en cristallographie

Abaque de Wulff, pas de 10°.

La projection stéréographique est utilisée pour représenter les formes cristallines des cristaux, leurs groupes ponctuels de symétrie, ainsi que l'orientation préférentielle des polycristaux. Le centre du cristal étudié est placé au centre d'une sphère imaginaire. C'est l'intersection avec cette sphère des éléments de symétrie du cristal ou des normales à ses faces qui est projetée sur le plan équatorial lors de la projection stéréographique.

On utilise pour la représentation un abaque de Wulff (du nom de George Wulff) muni d'un repère de coordonnées, au centre duquel est placé le cristal. Le choix du repère de coordonnées dépend de la symétrie du cristal et en particulier de ses directions de symétrie. Les vecteurs de base du repère de coordonnées dans le plan équatorial sont représentés par des marques extérieures au cercle de projection. La direction de plus haute symétrie est généralement choisie comme étant la direction nord-sud. Par exemple, dans le système cristallin quadratique, la direction [001] est choisie perpendiculaire au plan de projection.

Projection des éléments de symétrie

Pour la représentation graphique des groupes ponctuels de symétrie, le point à l'intersection des éléments de symétrie est placé au centre de la sphère. Dans certains cas, il n'existe pas un tel point ou il en existe une infinité : il s'agit des groupes 1, 2, m, mm2, 4, 4mm, 3, 3m, 6 et 6mm. On choisit alors généralement l'axe de plus haute symétrie ou la droite d'intersection des éléments de symétrie comme direction nord-sud de la sphère.

Les éléments de symétrie dans les groupes ponctuels sont de trois types : plans de réflexion, axes de rotation et axes de roto-inversion. Chaque élément de symétrie passe par le centre de la sphère.

Pour les plans miroirs, l'intersection d'un plan avec une sphère étant un cercle, trois cas se présentent :

• le plan miroir est parallèle au plan équatorial, sa projection stéréographique est le grand cercle extérieur représenté en bleu dans la figure du groupe 4/mmm ci-dessous ;
• le plan miroir est perpendiculaire au plan équatorial, sa projection est un segment ;
• le plan miroir est ni parallèle ni perpendiculaire au plan équatorial, sa projection consiste en deux arcs de cercle de même longueur et d'extrémités communes sur le grand cercle (« grand cercle intérieur »), tracés en bleu dans la représentation du groupe mModèle:Surlignerm ci-dessous.

L'intersection d'un axe de symétrie avec la sphère produit deux points diamétralement opposés, la projection stéréographique d'un axe de symétrie consiste donc en deux points. Les axes de symétrie sont représentés par des symboles définis dans les tables internationales de cristallographie.

• Si l'axe est perpendiculaire au plan équatorial, les deux points se confondent au centre du cercle de projection (axes 4 et Modèle:Surligner représentés en rouge dans les figures des groupes 4/mmm et Modèle:Surligner2m ci-dessous).
• Si l'axe est parallèle au plan équatorial, les deux points sont diamétralement opposés sur le grand cercle extérieur (axes 2 du groupe Modèle:Surligner2m dans la figure ci-dessous).
• Si l'axe est ni parallèle ni perpendiculaire au plan équatorial, les deux points sont à l'intérieur du cercle de projection et symétriques par rapport au centre du cercle (axes Modèle:Surligner du groupe mModèle:Surlignerm).

• 
  Groupe 4/mmm
• 
  Groupe Modèle:Surligner2m
• 
  Groupe mModèle:Surlignerm

Représentation des formes cristallines

Les faces des formes cristallines sont représentées par leurs normales. On ne considère que l'intersection de la normale avec la sphère qui est la plus proche de la face considérée. Cette intersection est appelée « pôle de la face ». Si un pôle est situé sur l'hémisphère nord de la sphère, il est représenté par une croix, sinon, par un cercle. La distinction entre les hémisphères n'est pas faite pour la représentation des éléments de symétrie.

Les figures ci-dessous montrent un tétraèdre et sa projection stéréographique avec les éléments de symétrie de son groupe, Modèle:Surligner3m. Les normales de ses faces sont confondues avec les axes de rotation d'ordre 3.

• 
• 

Photographie

Extrait rectangulaire d’une projection stéréographique du ciel de l’observateur (sphère centrée en l’appareil photographique) avec pour pôle de projection, le point de ce ciel situé au zénith de l’observateur.

Pour le rendu plan de photographies en grand angle, voire panoramiques, la projection stéréographique est souvent préférée à d’autres projections azimutales pour sa conformité : pas de déformation locale.

• 
  Projection équirectangulaire
• 
  Projection stéréographique

Voir aussi

Modèle:Autres projets Les trois autres projections azimutales principales :

• Projection orthographique
• Projection azimutale équivalente de Lambert
• Projection gnomonique

Articles connexes

• Figure de pôles
• Projection cartographique

Liens externes

• Vidéo pédagogique extaite d'une série de 9 épisodes sur la représentation des dimensions dans l'espace
• Animation de l‘American Mathematical Society montrant de manière esthétisée un portrait de Bernhard Riemann se déplaçant sur une sphère et projeté stéréographiquement en même temps sur un plan.
• Dandelin, Gergonne, Usages de la projection stéréographique en géométrie, Annales de mathématiques pures et appliquées, tome 16 (1825-1826), p. 322-327.