Quadrilatère inscriptible

Quadrilatères inscriptibles

En géométrie, un quadrilatère inscriptible (ou cyclique ) est un quadrilatère dont les sommets se trouvent tous sur un seul et même cercle. Les sommets sont dits cocycliques. Le quadrilatère est dit inscrit dans le cercle, et le cercle, circonscrit au quadrilatère.

Caractérisations

Par les médiatrices

Un quadrilatère convexe est inscriptible si et seulement si les quatre médiatrices des côtés sont concourantes. Le point de concours est alors le centre du cercle circonscrit et les médiatrices des diagonales passent par ce point.

Par les angles

$\hat{A}+\hat{C}=\pi$, $\hat{B}+\hat{D}=\pi$

$\hat{A}=\hat{C},\hat{B}=\hat{D}$

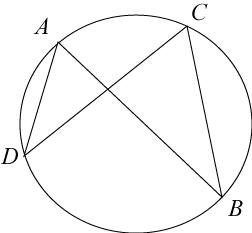
Un quadrilatère convexe est inscriptible si et seulement si les angles opposés sont supplémentaires (leur somme est Modèle:Math radians, soit 180°). Ou de façon équivalente, si et seulement si chaque angle externe est égal à l'angle interne opposé. Cette propriété est en fait une variante du théorème de l'angle inscrit et de l'angle au centre.

Un quadrilatère croisé est inscriptible si et seulement si ses angles opposés ont même mesure.

Existence

Théorème de Sturm Modèle:,: s'il existe un quadrilatère de longueurs de côtés successifs $a,b,c,d$, c'est-à-dire si $a⩽b+c+d,b⩽c+d+a,c⩽d+a+b,d⩽a+b+c$, alors il existe un quadrilatère convexe inscriptible ayant $a,b,c,d$ pour longueurs de côtés.

Cela signifie que les sommets de tout quadrilatère articulé peuvent être inscrits dans un cercle.

Aire

Quadrilatère inscriptible de côtés a, b, c et d.

L'aire Modèle:Mvar d'un quadrilatère convexe inscriptible en fonction des longueurs Modèle:Mvar, Modèle:Mvar, Modèle:Mvar et Modèle:Mvar de ses côtés successifs est donnée par la formule de Brahmagupta :

$S=\sqrt{(p-a)(p-b)(p-c)(p-d)}$

où Modèle:Math est le demi-périmètre.

D'après la formule de Bretschneider, un quadrilatère convexe ayant Modèle:Mvar, Modèle:Mvar, Modèle:Mvar Modèle:Mvar pour suite de longueurs des côtés possède une aire maximale lorsqu'il est inscriptible.

L'aire d'un quadrilatère convexe inscriptible est aussi donnée Modèle:Infra par :

$S=\frac{1}{2}(bc+ad)\sin \gamma$

où Modèle:Math est l'angle entre les côtés de longueurs Modèle:Mvar et Modèle:Mvar.

Diagonales

Le théorème de Ptolémée dit que le produit des longueurs Modèle:Mvar et Modèle:Mvar des deux diagonales d'un quadrilatère convexe inscriptible est égal à la somme des produits des longueurs des côtés opposés Modèle:Mvar et Modèle:Mvar :

$ef=ac+bd$.

Quadrilatère inscriptible avec ses deux diagonales de longueurs Modèle:Var et Modèle:Var, et ses triangles deux à deux semblables

Les deux diagonales d'un quadrilatère convexe le coupent en quatre triangles ; lorsque le quadrilatère est inscriptible, les paires de triangles opposés sont constituées chacune de deux triangles semblables.

Pour un quadrilatère convexe inscriptible de sommets successifs A, B, C, D, de côtés successifs a = AB, b = BC, c = CD et d = DA, et de diagonales e = AC et f = BD, on a (second théorème de Ptolémée):

$\frac{e}{f}=\frac{ad+cb}{ab+cd},e^2=\frac{(ac+bd)(ad+bc)}{ab+cd}\text{et}{f}^2=\frac{(ac+bd)(ab+dc)}{ad+bc}.$

Si le point d'intersection des diagonales divise une diagonale en segments de longueurs $e_1$ et $e_2$, et divise l'autre diagonale en segments de longueurs $f_1$ et $f_2$, alors $e_1{e}_2=f_1{f}_2$. (Ceci est valable parce que les deux diagonales sont des cordes d'un cercle.)

Cas particuliers

Tout rectangle est un trapèze isocèle, c'est-à-dire un trapèze circonscriptible. Un cerf-volant est inscriptible si et seulement s'il a deux angles droits (cerf-volant droit).

Autres propriétés

• Durant le Modèle:S-, le mathématicien Modèle:Lien détermina le rayon du cercle circonscrit d'un quadrilatère inscriptible. Notons les longueurs des côtés successifs Modèle:Mvar, Modèle:Mvar, Modèle:Mvar, Modèle:Mvar, le demi-périmètre Modèle:Mvar et l'aire Modèle:Mvar ; le rayon Modèle:Mvar s'obtient par la formule :

$R=\frac{1}{4}\sqrt{\frac{(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}=\frac{\sqrt{(ab+cd)(ac+bd)(ad+bc)}}{4S}$.

• Il n'existe pas de quadrilatère inscriptible dont l'aire est rationnelle et dont les longueurs des côtés sont rationnelles, inégales et forment une progression arithmétique ou géométrique.

• Les fonctions trigonométriques de l'angle Modèle:Math entre les côtés de longueurs Modèle:Mvar et Modèle:Mvar sont données par :

$\cos \gamma =\frac{a^2+d^2-b^2-c^2}{ad+bc}$ ;

$\sin \gamma =\frac{2S}{ad+bc}$ (Modèle:Mvar étant l'aire) ;

$\tan \frac{\gamma }{2}=\sqrt{\frac{(p-a)(p-d)}{(p-b)(p-c)}}$.

• Théorème de Jules Mathot (1901) : Dans un quadrilatère convexe inscriptible, les quatre droites passant par le milieu d'un côté et perpendiculaires au côté opposé sont concourantes. Le point de concours est le symétrique H du centre O du cercle circonscrit par rapport au centre de gravité des sommets (ou centre géométrique) G Modèle:ExpModèle:,Modèle:,.

Avec les notations A,B,C,D,I,J,K,L de la figure, soient O le centre du cercle circonscrit et G le centre de gravité des sommets. On sait que G est le milieu de la bimédiane [IK] ; si on note H le symétrique de O par rapport à G, le quadrilatère OIHG est un parallélogramme, ses diagonales se coupant en leur milieu. Or (OK) est perpendiculaire à (DC) donc également (IH) : la droite passant par I et perpendiculaire au côté opposé passe dont par H, et de même pour les trois autres.

Ces quatre droites sont appelées "maltitudes" en anglais (pour "midpoint-altitude"), ce que l'on peut traduire par "hauteurs médianes".

Certains auteurs considèrent la droite (OGH) comme la "droite d'Euler" du quadrilatère inscriptible .

• Théorème japonaisModèle:Article détaillé

Quadrilatères de Brahmagupta

Exemple de quadrilatère de Brahmagupta ; l'aire est égale à 966.

Un quadrilatère de BrahmaguptaModèle:,est un quadrilatère convexe inscriptible dont les longueurs des côtés, les longueurs des diagonales et l'aire sont des nombres entiers. On obtient tous les quadrilatères de Brahmagupta de longueurs de côtés Modèle:Math, Modèle:Math, Modèle:Math, Modèle:Math, de longueurs de diagonales Modèle:Math, Modèle:Math, d'aire Modèle:Math et de rayon circonscrit Modèle:Math, en supprimant les dénominateurs des expressions suivantes impliquant des paramètres rationnels $t=\tan \frac{\widehat{CAD}}{2}=\tan \frac{\widehat{CBD}}{2},u=\tan \frac{A}{2},v=\tan \frac{C}{2}$ :

$a=[t(u+v)+(1-uv)][u+v-t(1-uv)]$

$b=(1+u^2)(v-t)(1+tv)$

$c=t(1+u^2)(1+v^2)$

$d=(1+v^2)(u-t)(1+tu)$

$e=u(1+t^2)(1+v^2)$

$f=v(1+t^2)(1+u^2)$

$S=uv[2t(1-uv)-(u+v)(1-t^2)][2(u+v)t+(1-uv)(1-t^2)]$

$4R=(1+u^2)(1+v^2)(1+t^2).$

Propriétés des quadrilatères inscriptibles qui sont également orthodiagonaux

Dans un quadrilatère orthodiagonal (c'est-à-dire dont les diagonales sont perpendiculaires), les "hauteurs médianes" définies ci-dessus se coupent deux à deux sur des diagonales. Par exemple, les "hauteurs médianes" issues des milieux de [AD] et [AB] se coupent sur la diagonale issue de A.

Avec les notations A,B,C,D,I,J,K,L de la figure, soit M le milieu de la diagonale issue de A. D'après le théorème des milieux, le triangle IML a ses côtés parallèles à (BC), (CD), et (BD) . Donc les "hauteurs médianes" issues de I et L en sont deux hauteurs. Or la troisième hauteur, issue de M, n'est autre que la diagonale (AC) ( (IL) étant parallèle à (BD)). Les deux "hauteurs médianes" se coupent donc sur cette diagonale.

Par conséquent, d'après la propriété ci-dessus, dans un quadrilatère à la fois inscriptible et orthodiagonal, les quatre "hauteurs médianes" concourent au point d’intersection H des diagonales, appelé l'anticentre du quadrilatère inscriptible orthodiagonal .

On retrouve ainsi le théorème de Brahmagupta, affirmant que dans un quadrilatère inscriptible orthodiagonal, la perpendiculaire à n'importe quel côté passant par le point d'intersection des diagonales coupe l'autre côté en son milieuModèle:Exp.

Dans un quadrilatère inscriptible orthodiagonal :

• la distance du centre O du cercle circonscrit à n'importe quel côté est égal à la moitié de la longueur du côté opposéModèle:Exp,

• supposons que l'intersection des diagonales divise une diagonale en segments de longueurs Modèle:Math et Modèle:Math et divise l'autre diagonale en segments de longueurs Modèle:Math et Modèle:Math. Alors

$e_1^2+e_2^2+f_1^2+f_2^2=a^2+c^2=b^2+d^2=4R^2$

où $R$ est le rayon du cercle circonscrit. Cela est dû au fait que les diagonales sont des cordes perpendiculaires d'un cercle. De façon équivalente, la moyenne de Modèle:Math, Modèle:Math, Modèle:Math et Modèle:Math est égale à Modèle:Math. En outre, les équations Modèle:Math impliquent que la somme des carrés des côtés est égal à huit fois le carré du rayon du cercle circonscrit.

Le quotient du périmètre d'un cercle par celui d'un carré inscrit est égal à Modèle:Sfrac ≈ 1,110 720 (Modèle:OEIS).

Voir aussi

Articles connexes

• Quadrilatère bicentrique (à la fois inscriptible et circonscriptible)
• Théorème japonais pour les quadrilatères inscriptibles

Liens externes

• Modèle:En Derivation of Formula for the Area of Cyclic Quadrilateral sur mathalino.com
• Modèle:En Incenters in Cyclic Quadrilateral sur Cut The Knot
• Modèle:En Four Concurrent Lines in a Cyclic Quadrilateral sur Cut The Knot
• Modèle:MathWorld