Quadrilatère orthodiagonal

Exemples de quadrilatères orthodiagonaux non convexes.

En géométrie euclidienne, un quadrilatère orthodiagonal est un quadrilatère dont les diagonales se coupent à angle droit. Autrement dit, il s'agit d'un polygone à quatre côtés dont les segments entre sommets non adjacents sont perpendiculaires.

Exemples de quadrilatères orthodiagonaux convexes.

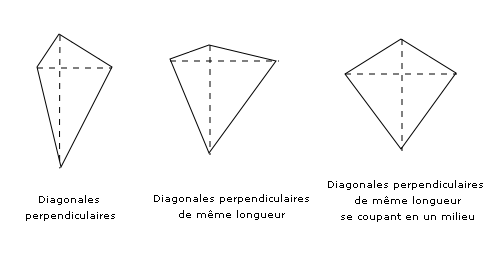
Cas particuliers

Un cerf-volant est un quadrilatère orthodiagonal dont l'une des diagonales est axe de symétrie. Les cerfs-volants sont les quadrilatères orthodiagonaux circonscriptibles, c'est-à-dire possédant un cercle inscrit tangent à chacun de leurs quatre côtés.

Un losange est un quadrilatère orthodiagonal ayant ses côtés parallèles deux à deux (c'est-à-dire un parallélogramme orthodiagonal).

Un carré est un quadrilatère qui est à la fois un cerf-volant et un losange.

Les quadrilatères à la fois orthodiagonaux et équidiagonaux sont dits de carré médian ou appelés des pseudo-carrés.

Les pseudo-carrés dans lesquels les diagonales sont au moins aussi longues que tous les côtés du quadrilatère sont d'aire maximale parmi tous les quadrilatères de diamètre donné, résolvant le cas Modèle:Mvar = 4 du problème du plus grand petit polygone. Le carré est l'un de ces quadrilatères, mais il en existe une infinité d'autres.

Un quadrilatère convexe orthodiagonal (en jaune). Les deux carrés rouges, construits sur deux côtés opposés du quadrilatère, ont la même aire totale que les deux carrés bleus sur l'autre paire de côtés opposés.

Caractérisations

La somme des carrés des longueurs de deux côtés opposés d'un quadrilatère convexe orthodiagonal, est égale à celle des deux autres côtés. Notant Modèle:Mvar et Modèle:Mvar, les longueurs successives des côtés, on aModèle:, :

$a^2+c^2=b^2+d^2.$

Cette relation est une conséquence directe du théorème de Pythagore, appliqué aux quatre triangles rectangles formés par les sommets du quadrilatère et le point d'intersection des diagonales.

La réciproque est également vraie : tout quadrilatère vérifiant $a^2+c^2=b^2+d^2$ est orthodiagonal. La démonstration se fait par exemple par la loi des cosinus. On en déduit qu'un quadrilatère articulé qui a une position orthodiagonale, reste orthodiagonal dans toutes ses déformations.

Les diagonales d'un quadrilatère convexe sont perpendiculaires si et seulement si les deux bimédianes ont même longueur.

Il existe une autre caractérisation à partir des angles : les diagonales d'un quadrilatère convexe Modèle:Mvar se coupant en Modèle:Mvar sont perpendiculaires si et seulement si

$\widehat{PAB}+\widehat{PBA}+\widehat{PCD}+\widehat{PDC}=\pi$.

De cette équation, on en déduit que les diagonales d'un quadrilatère convexe sont perpendiculaires si et seulement si les projections de l'intersection des diagonales sur les côtés du quadrilatère forment les sommets d'un quadrilatère inscriptible.

Un quadrilatère orthodiagonal Modèle:Mvar (en bleu). Le parallélogramme de Varignon (en vert) formé par les milieux des côtés de Modèle:Mvar est un rectangle. De plus, les quatre milieux (en gris) et les quatre pieds des "hauteurs médianes" (en rouge) sont cocycliques sur le cercle des 8 points.

Un quadrilatère convexe est orthodiagonal si et seulement si son parallélogramme de Varignon (formé par les milieux de ses côtés) est un rectangle. On en déduit une autre caractérisation : un quadrilatère convexe est orthodiagonal si et seulement si les milieux des côtés et les pieds des quatre "hauteurs médianes" (joignant le milieu d'un côté au projeté sur le côté opposé, dénommées maltitudes en anglais) sont huit points cocycliques ; le cercle commun à ces points est appelé premier cercle des huit points Modèle:,Modèle:,. Le centre de ce cercle est le centre de gravité du quadrilatère. Le quadrilatère formé par les pieds des "hauteurs médianes" est appelé quadrilatère orthique principal.

Un deuxième cercle des 8 points peut être construit à partir d'un quadrilatère orthodiagonal Modèle:Mvar (en bleu). Les droites perpendiculaires aux côtés passant par le point d'intersection des diagonales coupent les côtés en 8 points différents, qui sont tous cocycliques.

Si les perpendiculaires aux côtés d'un quadrilatère convexe Modèle:Mvar passant par l'intersection des diagonales coupent les côtés opposés en R, S, T, U ; et que K, L, M, N sont les pieds de ces perpendiculaires, alors Modèle:Mvar est orthodiagonal si et seulement si les huit points K, L, M, N, R, S, T et U sont cocycliques sur le second cercle des huit points. Par corollaire, un quadrilatère convexe est orthodiagonal si et seulement si Modèle:Mvar est un rectangle dont les côtés sont parallèles aux diagonales de Modèle:Mvar.

Il existe plusieurs caractérisations par les longueurs des côtés des triangles formés par le point d'intersection Modèle:Mvar des diagonales et deux sommets consécutifs d'un quadrilatère convexe Modèle:Mvar. Soient m₁, m₂, m₃, m₄ les médianes issues de Modèle:Mvar respectives des triangles ABP, BCP, CDP, DAP . Si R₁, R₂, R₃, R₄ et h₁, h₂, h₃, h₄ désignent respectivement les rayons des cercles circonscrits et les hauteurs de ces triangles, alors le quadrilatère convexe Modèle:Mvar est orthodiagonal si et seulement si au moins l'une des égalités suivantes est vraie :

• $m_1^2+m_3^2=m_2^2+m_4^2$
• $R_1^2+R_3^2=R_2^2+R_4^2$
• $\frac{1}{h_1^2}+\frac{1}{h_3^2}=\frac{1}{h_2^2}+\frac{1}{h_4^2}$.

De plus, un quadrilatère convexe Modèle:Mvar, dont les diagonales se coupent en Modèle:Mvar est orthodiagonal si et seulement si les centres des cercles circonscrits des triangles ABP, BCP, CDP et DAP sont les milieux des côtés du quadrilatère.

Comparaison avec les quadrilatères circonscriptibles

Certaines caractérisations métriques des quadrilatères circonscriptibles et des quadrilatères convexes orthodiagonaux sont très similaires, comme on peut le voir dans le tableau ci-dessous. Les notations des longueurs des côtés a, b, c, d, les rayons des cercles circonscrits R₁, R₂, R₃, R₄, et les hauteurs h₁, h₂, h₃, h₄ sont les mêmes que ci-dessus dans les deux types de quadrilatères.

Quadrilatère circonscriptible	Quadrilatère orthodiagonal
$a+c=b+d$	$a^2+c^2=b^2+d^2$
$R_1+R_3=R_2+R_4$	$R_1^2+R_3^2=R_2^2+R_4^2$
$\frac{1}{h_1}+\frac{1}{h_3}=\frac{1}{h_2}+\frac{1}{h_4}$	$\frac{1}{h_1^2}+\frac{1}{h_3^2}=\frac{1}{h_2^2}+\frac{1}{h_4^2}$

Aire

L'aire Modèle:Mvar d'un quadrilatère orthodiagonal non croisé est égale à la moitié du produit des longueurs Modèle:Mvar et Modèle:Mvar des diagonales  :

$S=\frac{pq}{2}.$

Réciproquement, tout quadrilatère convexe dont l'aire vérifie cette relation est nécessairement orthodiagonal.

Étant données deux longueurs Modèle:Mvar et Modèle:Mvar, les quadrilatères ayant Modèle:Mvar et Modèle:Mvar pour longueurs de diagonales ont une aire maximale (égale à $pq/2$) lorsqu'ils sont orthodiagonaux. On en déduit que les quadrilatères de diamètre donné ont une aire maximale lorsqu'ils sont ortho- et équi-diagonaux (des pseudo-carrés) .

Autres propriétés

• Les quadrilatères convexes orthodiagonaux sont les seuls quadrilatères convexes pour lesquels les longueurs des côtés et l'angle formé par les diagonales ne déterminent pas uniquement l'aire. Par exemple, soient deux losanges ayant même longueur de côté. Leurs diagonales se coupent à angle droit, mais si l'un a un angle aigu plus petit que celui de l'autre, alors ils auront des aires différentes (l'aire du premier tendant vers zéro lorsque l'angle aigu tend vers zéro).
• Le théorème de Van Aubel affirme que pour un quadrilatère convexe quelconque, si l'on construit vers l'extérieur un carré à partir de chacun de ses côtés, les centres des quatre carrés ainsi construits forment un quadrilatère à la fois équidiagonal et orthodiagonal.
• Chaque côté d'un quadrilatère convexe orthodiagonal a au moins un point commun avec le cercle des points de Pascal.

Quadrilatères orthodiagonaux inscriptibles

Rayon du cercle circonscrit et aire

On suppose que le point d'intersection des diagonales d'un quadrilatère orthodiagonal inscriptible (dont les sommets appartiennent à un même cercle) divise celles-ci en segments de longueurs respectives p₁, p₂ et q_1, q₂ ; alors, d'après la proposition 11 du Livre des Lemmes d'Archimède:

$D^2=p_1^2+p_2^2+q_1^2+q_2^2=a^2+c^2=b^2+d^2$,

où Modèle:Mvar est le diamètre du cercle circonscrit. La relation se déduit du fait que les diagonales forment des cordes perpendiculaires d'un cercle. On obtient alors une expression du rayon du cercle circonscrit Modèle:Mvar :

$R=\frac{1}{2}\sqrt{p_1^2+p_2^2+q_1^2+q_2^2}$,

soit en fonction des longueurs des côtés du quadrilatère,

$R=\frac{1}{2}\sqrt{a^2+c^2}=\frac{1}{2}\sqrt{b^2+d^2}.$

On a alors

$a^2+b^2+c^2+d^2=8R^2.$

Ainsi, d'après la relation d'Euler dans le quadrilatère, le rayon du cercle circonscrit peut être exprimé en termes des longueurs des diagonales Modèle:Mvar et Modèle:Mvar, et de la distance Modèle:Mvar entre les milieux des diagonales :

$R=\sqrt{\frac{p^2+q^2+4x^2}{8}}.$

On déduit également la formule de l'aire Modèle:Mvar d'un quadrilatère orthodiagonal inscriptible en fonction des quatre côtés en combinant le théorème de Ptolémée et la formule de l'aire d'un quadrilatère orthodiagonal vue ci-dessus. On a finalement :

$S=\frac{1}{2}(ac+bd).$

Autres propriétés

Dans un quadrilatère orthodiagonal inscriptible :

• l'anticentre (symétrique du centre du cercle circonscrit par rapport au centre de gravité) est confondu avec le point d'intersection des diagonales,
• la perpendiculaire à un côté passant par le point d'intersection des diagonales coupe le côté opposé en son milieu (théorème de Brahmagupta),
• la distance du centre du cercle circonscrit à n'importe quel côté est égale à la moitié de la longueur du côté opposé
• la distance entre les milieux des diagonales est égale à la distance entre le centre circonscrit et le point d'intersection des diagonales.

  

  Quadrilatère de Brahmagupta.

Exemple : le quadrilatère de Brahmagupta

Le mathématicien indien Brahmagupta découvrit un quadrilatère orthodiagonal inscriptible, formé de 4 triangles pythagoriciens, à côtés et diagonales entiersModèle:,.

$ABCD$ est un quadrilatère orthodiagonal. $P_1$ et $Q_1$ sont des points de Pascal formés par le cercle ${\omega }_1$, ${\sigma }_{P_1{Q}_1}$ est le cercle des points de Pascal qui définit le rectangle $P_1{V}_1{Q}_1{W}_1$ . $P_2$ et $Q_2$ sont des points Pascal formés par le cercle ${\omega }_2$, ${\sigma }_{P_2{Q}_2}$ est le cercle aux points de Pascal qui définit le rectangle $P_2{V}_2{Q}_2{W}_2$ .

Ensembles infinis de rectangles inscrits

$ABCD$ est un quadrilatère orthodiagonal, $P_1{X}_1{Z}_1{Y}_1$ et $P_2{X}_2{Z}_2{Y}_2$ sont des rectangles dont les côtés sont parallèles aux diagonales du quadrilatère.

On peut inscrire dans tout quadrilatère convexe orthodiagonal deux ensembles infinis de rectangles :

• un ensemble de rectangles dont les côtés sont parallèles aux diagonales du quadrilatère
• un ensemble de rectangles définis par des cercles de points de Pascal.