Théorème de factorisation
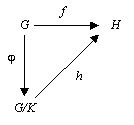
En mathématiques, le théorème de factorisation est un principe général qui permet de construire un morphisme d'une structure quotient dans un autre espace à partir d'un morphisme de vers , de façon à factoriser ce dernier par la surjection canonique de passage au quotient.
Le cas des ensembles
Soit un ensemble muni d'une relation d'équivalence et la surjection canonique.
- L'unicité de g est immédiate et guide la preuve de son existence, dont voici plusieurs variantes :
- Preuve « naïve » : pour tout élément , on pose . Si pour un élément équivalent à , on a par hypothèse. Donc est bien définie. Par construction, f = g∘s.
- Formalisation de la preuve « naïve », rendant plus manifeste l'utilisation de l'axiome du choix : soit t une section de s (c'est-à-dire une application qui à chaque classe associe un élément de cette classe). On pose g = f∘t. Alors, pour tout élément x de X, (t∘s)(x) R x donc f((t∘s)(x)) = f(x), c'est-à-dire (g∘s)(x) = f(x) ; on a donc bien f = g∘s[1].
- Preuve sans axiome du choix : par hypothèse, f envoie tous les éléments d'une classe z sur un même élément y de Y. L'assignation z ↦ y définit alors l'application g qui convient[2].
- Formalisation de la preuve sans axiome du choix : en notant F et S les graphes de f et s, la [[Relation binaire#Composition et réciproque|relation binaire G = F ∘ SModèle:-1]] (définie par : zGy s'il existe un x tel que z = s(x) et f(x) = y) est fonctionnelle et définit l'application g qui convient.
- Si f est surjective, l'égalité f = g∘s implique que g est aussi surjective.
- Supposons que est équivalent à . Soient tels que . Alors , donc et . Ce qui veut dire que est injective.
- La dernière propriété résulte des deux précédentes.
(La réciproque est moins utile mais immédiate : pour toute application g : X/R → Y, la composée f = g∘s vérifie x R xModèle:' ⇒ f(x) = f(xModèle:').)
Ce théorème peut se spécialiser à un certain nombre de structures algébriques ou topologiques.
Le cas des groupes
Modèle:Voir Sur un groupe , on considère la relation d'équivalence définie par un sous-groupe normal de : si . Alors, la surjection canonique est un morphisme de groupes et le théorème de factorisation s'énonce
Le cas des espaces vectoriels
On considère un espace vectoriel et la relation d'équivalence définie par un sous-espace vectoriel : si . Alors, la surjection canonique est linéaire.
Le cas des anneaux
Modèle:Voir On considère un anneau et la relation d'équivalence définie par un idéal bilatère de : si . Alors, la surjection canonique est un morphisme d'anneaux.
Le cas des espaces topologiques
Soit un espace topologique muni d'une relation d'équivalence et la surjection canonique. On munit de la topologie quotient. Soit une application continue.
Références
Article connexe
- ↑ Modèle:Bourbaki-Ensembles, Modèle:P., C57, renvoyant à Modèle:Google Livres, proposition 9.a.
- ↑ Modèle:MacLaneBirkhoff1, Modèle:Google Livres.