Polyèdre de coordination

La notion de polyèdre de coordination est utilisée en cristallographie et en chimie pour décrire l'environnement d'une espèce chimique par ses ligands dans un cristal ou un complexe. Il s'agit du polyèdre formé par les ligands autour de l'espèce chimique centrale. La coordinence, c'est-à-dire le nombre de ligands, n'est pas suffisante pour décrire l'environnement d'une espèce chimique, car pour une coordinence donnée, il peut exister plusieurs polyèdres de coordination. Par exemple, à l'état solide, le cuivre a une coordinence 4 d'oxygène dans le silicate de baryum et de cuivre Modèle:Chem et également une coordinence 4 de soufre dans la stannite Modèle:Chem, mais son polyèdre de coordination est un carré CuOModèle:Ind dans Modèle:Chem et un tétraèdre CuSModèle:Ind dans la stannite.

En solution, la notion de coordinence est souvent réduite à la coordinence des cations (les anions sont coordonnés avec une énergie de liaison faible qui ne donne pas une bonne stabilité à la structure). La coordinence est définie, comme à l'état solide, par l'environnement du cation dans sa première sphère de coordination. Celle-ci est définie par les ligands (éventuellement le solvant) qui sont directement liés au cation. Ces ligands sont géométriquement orientés, et leur liaison est raisonnablement forte pour que les échanges avec les entités de la seconde sphère de coordination soient lents. Cette seconde sphère est surtout constituée de molécules de solvant, mais pas exclusivement, qui sont orientées par la présence du cation, mais qui s'échangent (1) rapidement avec les molécules de solvant qui lui sont extérieures, et (2) lentement avec les ligands qui lui sont intérieurs. La géométrie de la coordinence d'un cation en solution est moins variée qu'à l'état solide. Avec les ligands courants, la plupart des cations métalliques adoptent une coordinence octaédrique, une faible part adopte une coordinence tétraédrique ou plan carré, et les métaux de la colonne du cuivre au degré d'oxydation I ont une coordinence deux (linéaire). De ces derniers, l'ion diammine argent Modèle:Fchim⁺ (appelé aussi réactif de Tollens) est le plus connu. Les coordinences autres résultent de la présence de ligands particuliers (par exemple encombrants), ou de cations métalliques de grosse taille (Ta, WModèle:Etc.)

Les polyèdres de coordination possibles pour une espèce chimique donnée et ses ligands dépendent du degré d'oxydation de l'espèce chimique et des rayons ioniques mis en jeu, plus précisément du rapport $r_c/r_a$ où $r_c$ est le rayon ionique de l'espèce chimique centrale et $r_a$ le rayon de ses ligands.

Les polyèdres de coordination ne sont en général pas réguliers. Par exemple, dans le cas des complexes, ils peuvent présenter une déformation due à la configuration électronique du cation métallique dans le champ cristallin créé par les ligands. C'est le cas de Modèle:Fchim²⁺ qui présente une distorsion axiale qui s'explique par l'Effet Jahn-Teller. Un autre cas de non régularité est celui de la nature chimiques différentes des ligands, comme avec Modèle:Fchim²⁺. Dans tous les cas, il est cependant d'usage d'utiliser le nom des polyèdres réguliers pour décrire la coordination des espèces chimiques.

Les différents polyèdres de coordination

Les polyèdres de coordination sont généralement constitués de faces triangulaires équilatérales, comme le tétraèdre, l'octaèdre, la bipyramide trigonale ou l'icosaèdre. On rencontre aussi souvent des faces carrées, comme dans la pyramide tétragonale, le cube ou le cuboctaèdre. Il est plus rare de trouver des polyèdres de coordination dont les faces possèdent un grand nombre de sommets.

Le tableau suivant donne les polyèdres de coordination rencontrés dans les complexes en solution et dans les cristaux :

Coordinence	Polyèdre	Représentation	Exemples : structure moléculaire	Exemples : état solide
2	linéaire		Cu dans l'ion diméthylcuprate(I) Modèle:Fchim−	Ag dans le dicyanoargentate(I) de potassium Modèle:Fchim
3	triangle		B dans le trifluorure de bore Modèle:Fchim	NOModèle:Ind dans le salpêtre KNOModèle:Ind, BOModèle:Ind, COModèle:Ind dans la calcite CaCOModèle:Ind
4	tétraèdre		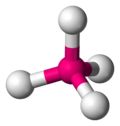Ni dans le tétracarbonylnickel(0) Modèle:Fchim	SiOModèle:Ind dans le quartz SiOModèle:Ind, BOModèle:Ind
	carré		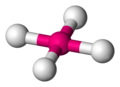Ni dans l'ion tétracyanonickelate(II) Modèle:Fchim2−	Cu dans CuO
5	bipyramide trigonale		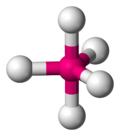Fe dans le pentacarbonylfer(0) Modèle:Fchim	K dans KModèle:IndSb
	pyramide tétragonale		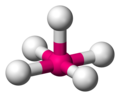Pas de structure courante simple, mais c'est une structure classique intermédiaire dans une substitution sur un complexe plan-carré (par addition du ligand entrant) ou pour dans une substitution sur un complexe octaédrique (après le départ du ligand sortant)	V dans Modèle:Chem, Ti dans la fresnoïte Modèle:Chem
6	octaèdre		Ti dans l'ion hexaaquatitane(II) Modèle:Fchim2+	Na et Cl dans NaCl, Ti dans BaTiOModèle:Ind (structure pérovskite), Ni dans la breithauptite NiSb
	prisme triangulaire ou trigonal			Sb dans la breithauptite
7	bipyramide pentagonale		U dans l'ion Modèle:Fchim	Pa dans PaClModèle:Ind
	octaèdre à face coiffée		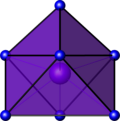	La dans A-Modèle:Chem
	prisme trigonal à face carrée coiffée
8	cube			Cs et Cl dans CsCl
	antiprisme carré ou tétragonal
	bipyramide hexagonale		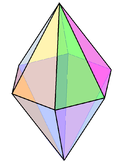	N dans LiModèle:IndN
	disphénoïde adouci			Zr dans Modèle:Chem
	prisme trigonal à deux faces triangulaires coiffées
	prisme trigonal à deux faces carrées coiffées			Ca dans Modèle:Chem
9	prisme trigonal à trois faces carrées coiffées			Pr dans Modèle:Chem, Sr dans Modèle:Chem
	antiprisme carré à face carrée coiffée			La dans LaTeModèle:Ind
10	antiprisme carré à faces coiffées
11
12	icosaèdre			Cr dans Modèle:Chem
	cuboctaèdre			Les atomes dans les métaux à structure de type empilement compact cubique à faces centrées
	orthobicoupole hexagonale ou anticuboctaèdre			Les atomes dans les métaux à structure de type empilement compact hexagonal
	prisme hexagonal			Rb dans Modèle:Chem

Détermination d'un polyèdre de coordination

Bipyramide trigonale idéalisée. Les arêtes épaisses correspondent aux angles diédraux de 53,1°, les arêtes plus fines aux angles diédraux de 101,5°. Les faces ne sont pas des triangles équilatéraux.

Dans la pratique, les polyèdres de coordination dans les matériaux cristallins sont souvent déterminés à partir d'expériences de diffraction de rayons X, de neutrons ou d'électrons. Des méthodes de spectroscopie comme la spectrométrie d'absorption des rayons X peuvent aussi donner des informations sur l'environnement des espèces chimiques, en particulier lorsqu'elles se trouvent en solution liquide ou dans un matériau amorphe.

Dans le cas des complexes métalliques synthétisés en solution, la coordinence n'est complètement établie qu'une fois la structure cristallographique résolue. Il est alors intéressant d'analyser les écarts entre les angles du polyèdre de base (par exemple l'octaèdre) et les angles effectivement observés. Ils sont souvent dus à des contraintes stériques. Il en est de même pour les distances cations - ligands. La déformation des distances pour des ligands de dimension comparable peut être interprétée par l'effet Jahn Teller. C'est le cas fréquent du cuivre(II). La géométrie la plus symétrique en solution, qui est généralement acceptée en bon accord avec les données RMN, n'est qu'une moyenne entre les différentes formes qui s'échangent les unes les autres par vibration de la sphère de complexation.

Les polyèdres de coordination sont en général décrits dans les publications scientifiques par la longueur des liaisons chimiques entre le cation central M et ses ligands X, et par les angles entre ces liaisons. La longueur des liaisons dépend des espèces chimiques considérées : dans un tétraèdre SiOModèle:Ind, les liaisons Si-O ont typiquement une longueur de Modèle:Unité, alors que les liaisons B-O moyennes dans un tétraèdre BOModèle:Ind varient entre Modèle:Unité et Modèle:Unité. Pour cette raison, on utilise d'abord les angles de liaison pour déterminer le polyèdre de coordination. Les longueurs de liaisons sont surtout utiles pour calculer le nombre de coordination effectif d'un atome ou pour rendre compte de la multiplicité de la liaison entre le cation métallique et un ligand.

Lorsqu'il y a déformation du polyèdre de coordination, c'est-à-dire lorsque les angles de liaisons observés s'écartent beaucoup des valeurs attendues pour un polyèdre régulier, il n'est pas toujours évident de reconnaître d'emblée le polyèdre de coordination d'un atome. Par exemple, le polyèdre de coordination CuOModèle:Ind du cuivre peut être une pyramide tétragonale dans le supraconducteur [[Oxyde mixte de baryum de cuivre et d'yttrium|Modèle:Chem]] ou une bipyramide trigonale dans l'olivénite Modèle:Chem, mais il est tellement déformé dans Modèle:Chem qu'il est à mi-chemin entre les deuxModèle:,. Le calcul des angles diédraux du polyèdre de coordination, entre les normales à deux faces adjacentes, permet dans certains cas difficiles de lever le doute. À chaque arête du polyèdre de coordination correspond un angle diédral. Le tableau suivant donne les angles de liaison et les angles diédraux pour quelques polyèdres de coordination idéalisés, pour lesquels toutes les longueurs de liaison M-X sont égales (les polyèdres de coordination ne sont alors pas forcément réguliers, voir le cas de la bipyramide trigonale).

Polyèdre	Angles de liaison X-M-X	Angles diédraux
carré	90° (×4)	0° (×4)
tétraèdre	109,5° (×4)	109,5° (×6)
pyramide tétragonale	90° (×8)	0° (×1), 75,7° (×4), 119,8° (×4)
bipyramide trigonale	120° (×3), 90° (×6)	53,1° (×3), 101,5 (×6)
cube	70,5° (×12)	90° (×12)
octaèdre	90° (×12)	70,5° (×12)

Facteurs déterminant les polyèdres de coordination

Pour une espèce chimique centrale et ses ligands donnés, le nombre de polyèdres de coordination possibles est restreint par plusieurs facteurs, en rapport avec les règles de Pauling.

Influence des rayons ioniques

Quelques quotients critiques

Polyèdre	Quotient critique
triangle équilatéral	$\frac{2\sqrt{3}-3}{3}=0,155$
tétraèdre	$\sqrt{\frac{3}{2}}-1=0,225$
carré, octaèdre	$\sqrt{2}-1=0,414$
prisme trigonal	$\sqrt{\frac{7}{3}}-1=0,528$
antiprisme tétragonal	$\sqrt{2+\frac{\sqrt{2}}{2}}-1=0,645$
cube	$\sqrt{3}-1=0,732$
icosaèdre	$0,902$
cuboctaèdre, anticuboctaèdre	$1$

Dans une description géométrique simplifiée, l'espèce chimique centrale (généralement un cation) et ses ligands (généralement des anions) sont considérés comme des boules dures de rayons ioniques $r_c$ et $r_a$, respectivement. Cette description est surtout valable pour des ligands monoatomiques. Dans le cas de ligands polyatomiques comme les bipyridines, il pourrait être possible de ne considérer que les atomes en contact direct avec l'espèce chimique centrale ; cependant, la forme de la molécule ligand aura une influence sur la taille du polyèdre de coordination.

Les ligands sont en contact avec l'espèce chimique centrale. Ils peuvent aussi toucher les autres ligands adjacents, mais pas nécessairement. La taille du site formé par les ligands en contact dans un polyèdre de coordination donne une limite inférieure pour la taille du cation qui s'y loge. Un cation ne peut pas se loger dans le site formé par les ligands si sa taille est plus petite que celle du site, car dans ce cas il n'est pas en contact direct avec les ligands : les répulsions électrostatiques entre les ligands l'emportent et la structure cristalline n'est plus stable.

Le calcul du quotient des rayons ioniques $q=r_c/r_a$ permet de déterminer le polyèdre de coordination probable d'une espèce chimique : il suffit de comparer $q$ aux quotients « critiques » $q_p$ pour tous les polyèdres de coordination. Au-delà de $q_p$, le polyèdre de coordination considéré n'est plus stable et il est probable que l'espèce chimique adoptera l'environnement possédant un quotient critique supérieur. Par exemple, dans le cas du quartz SiOModèle:Ind, le cation SiModèle:Exp a un rayon ionique $r_c$ de Modèle:Unité et l'anion OModèle:Exp un rayon ionique $r_a$ de Modèle:Unité, le quotient $q$ vaut 0,293 et le polyèdre de coordination du silicium est donc un tétraèdre SiOModèle:Ind.

Les polyèdres de coordination à haut quotient critique correspondent généralement à une grande coordinence, cependant, la coordinence n'augmente pas forcément avec le quotient critique : le carré (coordinence 4) et l'octaèdre (coordinence 6) possèdent le même quotient critique.

Le quotient critique $q_p$ est une caractéristique du polyèdre de coordination considéré et peut être calculé exactement de façon simple.

Coordination de type plan carré.

Considérons par exemple le cas de la coordination de type plan carré.

Les centres des ligands constituent un carré de côté $a$. Il suffit de déterminer l'arête du polyèdre de coordination et sa demi-diagonale en fonction des rayons ioniques $r_a$ et $r_c$ :

$\begin{array}{c}a=2r_a\\ \frac{a\sqrt{2}}{2}=r_a+r_c\end{array}$

En remplaçant $a$ par son expression en fonction de $r_a$, on obtient

$r_a+r_c=r_a\sqrt{2}$

d'où le quotient critique

$q_p=\frac{r_c}{r_a}=\sqrt{2}-1.$

La méthode de calcul du quotient critique présentée ici pour le carré fonctionne également pour les autres polyèdres de coordination.

Influence des degrés d'oxydation

Le changement du degré d'oxydation d'une espèce chimique a des conséquences sur son polyèdre de coordination. L'effet du degré d'oxydation sur l'environnement chimique n'est pas trivial. D'une part, un cation à haut degré d'oxydation aura tendance à attirer un grand nombre d'anions afin de compenser les charges électrostatiques. D'autre part, le rayon ionique d'un cation diminue lorsqu'il perd plus d'électrons, favorisant un polyèdre de coordination à plus faible quotient critique. Enfin, pour un même degré d'oxydation, une espèce chimique peut avoir plusieurs polyèdres de coordination différents.

Il existe cependant des corrélations entre degré d'oxydation et polyèdre de coordination, notamment pour les métaux de transition :

• cas du vanadium :
  • le cation VModèle:Exp possède une coordination octaédrique d'anions OModèle:Exp ;
  • le cation VModèle:Exp, de spin 1/2, peut être en coordination pyramidale tétragonale ou octaédrique d'OModèle:Exp ;
  • le cation VModèle:Exp peut être en coordination tétraédrique, pyramidale tétragonale ou octaédrique d'OModèle:Exp ;
• cas du cuivre :
  • le polyèdre de coordination du cation CuModèle:Exp est linéaire (groupes CuOModèle:Ind dans la cuprite CuModèle:IndO, le semi-conducteur Modèle:Chem) ou tétraédrique (groupes CuSModèle:Ind dans la stannite Modèle:Chem) ;
  • le polyèdre de coordination du cation CuModèle:Exp (spin 1/2) est très souvent un plan carré (groupes CuOModèle:Ind dans Modèle:Chem), une pyramide tétragonale (groupes CuOModèle:Ind dans le supraconducteur [[Oxyde mixte de baryum de cuivre et d'yttrium|Modèle:Chem]]), un octaèdre (groupes Modèle:Chem dans la mitscherlichite Modèle:Chem) ou, plus rarement, une bipyramide trigonale (groupes CuOModèle:Ind dans l'olivénite Modèle:Chem). Dans le cas de CuModèle:Exp, l'effet Jahn-Teller conduit à une forte déformation du polyèdre de coordination au-delà du carré.

Pour les complexes en solution, l'influence du degré d'oxydation s'inteprète souvent avec des arguments orbitalaires. Par exemple, la coordinence du cuivre(II) est un octaèdre déformé (élongation de symétrie DModèle:Ind due à l'effet Jahn Teller). C'est le cas par exemple de Modèle:FchimModèle:Exp. En revanche, le cuivre(I) a une coordinence linéaire. C'est le cas des organocuprates Modèle:FchimModèle:Exp. Il en est de même pour l'argent(I) avec le réactif de Tollens Modèle:FchimModèle:Exp et les complexes d'or(I).

Déformation d'un polyèdre de coordination

La déformation d'un polyèdre de coordination MXModèle:Ind est donnée principalement par la déviation des angles de liaison X-M-X par rapport à ceux des polyèdres idéalisés et par la distribution des longueurs de liaison, mais aussi par la distribution des distances entre les ligands.

Coordination tétraédrique

Trois paramètres sans dimension sont couramment utilisés pour décrire la déformation d'un tétraèdre MXModèle:Ind :

• BLD (déformation des longueurs de liaison, bond length distortion en anglais) :

$\text{BLD}=\frac{100}{n}\sum _{i=1}^n\frac{|(\text{M–X}{)}_i-<\text{M–X}>|}{<\text{M–X}>}\mathrm{\%}$

où (M–X)Modèle:Ind est la longueur de liaison entre l'espèce chimique centrale M et le ligand X, <M–X> est la moyenne des longueurs de liaison du tétraèdre et $n$ est le nombre de liaisons dont la longueur dévie de la longueur moyenne de plus d'une fois et demi l'écart-type sur sa valeur ;

• AD (déformation angulaire, angular distortion) :

$\text{AD}=\sum _{j=1}^n\frac{|a_j|}{n}\cdot 100\mathrm{\%}$

avec

$a_j=\sum _{i=1}^3\frac{{\alpha }_i-{\alpha }_0}{{\alpha }_0}\cdot 100\mathrm{\%}$

où ${\alpha }_0$ est l'angle de liaison dans le tétraèdre idéalisé, la somme sur $i$ se faisant sur les trois angles adjacents à la liaison considérée ;

• ELD (déformation des côtés du tétraèdre, edge length distortion) :

$\text{ELD}=\frac{100}{n}\sum _{i=1}^n\frac{|(\text{X–X}{)}_i-<\text{X–X}>|}{<\text{X–X}>}\cdot 100\mathrm{\%}$

où $n$ est cette fois le nombre de côtés du tétraèdre, soit 6.

Voir aussi

Articles connexes

• Complexe (chimie)
• Coordinence