4-polytope régulier convexe

Un hypercube.

Un polytope à 4 dimensions (ou polychore) régulier convexe est un objet géométrique, analogue en 4 dimensions des solides de Platon de la géométrie en 3 dimensions et des polygones réguliers de la géométrie en 2 dimensions.

Ces polytopes furent décrits la première fois en parallèle par le mathématicien suisse Ludwig Schläfli et par la mathématicienne autodidacte irlandaise Alicia Boole Stott, au milieu du Modèle:XIXe siècle. Schläfli et Boole Stott découvrirent, sans avoir conscience des travaux de l'autre, qu'il y avait précisément six figures de ce type. Cinq d'entre elles sont considérées comme les analogues de dimension 4 des solides de Platon. Il y a une figure supplémentaire (l'icositétrachore) qui n'a aucun équivalent tri-dimensionnel.

Chaque polytope régulier convexe à 4 dimensions est limité par des cellules tri-dimensionnelles qui sont toutes des solides de Platon du même type et de même taille. Ceux-ci sont organisés ensemble le long de leurs côtés de manière régulière.

Ils sont tous homéomorphes à une hypersphère à la surface tri-dimensionnelle ; leur caractéristique d'Euler-Poincaré vaut donc 0.

Propriétés

Caractéristiques

Le tableau suivant résume les caractéristiques principales des polychores réguliers :

• Symbole de Schläfli
• Nombre de sommets, d'arêtes, de faces et de cellules
• Figure de sommet
• Polychore dual
• Groupe de Coxeter et ordre du groupe

Polychore	Symbole de Schläfli	Sommets	Arêtes	Faces	Cellules	Figure de sommet	Dual	Groupe de Coxeter	Ordre
Pentachore	{3,3,3}	5	10	10 (triangles)	5 (tétraèdres)	Tétraèdre	(Lui-même)	A4	120
Tesseract	{4,3,3}	16	32	24 (carrés)	8 (cubes)	Tétraèdre	Hexadécachore	B4	384
Hexadécachore	{3,3,4}	8	24	32 (triangles)	16 (tétraèdres)	Octaèdre	Tesseract	B4	384
Icositétrachore	{3,4,3}	24	96	96 (triangles)	24 (octaèdres)	Cube	(Lui-même)	F4	1 152
Hécatonicosachore	{5,3,3}	600	1 200	720 (pentagones)	120 (dodécaèdres)	Tétraèdre	Hexacosichore	H4	14 400
Hexacosichore	{3,3,5}	120	720	1 200 (triangles)	600 (tétraèdres)	Icosaèdre	Hécatonicosachore	H4	14 400

Dimensions

Le tableau suivant résume certaines propriétés géométriques des polychores réguliers :

• V : hypervolume
• S : hypersurface
• R : rayon de la 3-sphère circonscrite
• r : rayon de la 3-sphère inscrite (r)
• θ : angle dichoral

Dans les formules, φ est le nombre d'or et l'arête est de longueur unité.

Polychore	V	S	R	r	θ
Pentachore	$\frac{\sqrt{5}}{96}$	$\frac{5\sqrt{2}}{12}$	$\frac{\sqrt{10}}{5}$	$\frac{\sqrt{10}}{20}$	$\arccos \frac{1}{4}$
Tesseract	$1$	$8$	$1$	$\frac{1}{2}$	$\frac{\pi }{2}$
Hexadécachore	$\frac{1}{6}$	$\frac{4\sqrt{2}}{3}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{4}$	$\frac{2\pi }{3}$
Icositétrachore	$2$	$8\sqrt{2}$	$1$	$\frac{\sqrt{2}}{2}$	$\frac{2\pi }{3}$
Hécatonicosachore	$\frac{15(47\phi +29)}{2}$	$60(7\phi +4)$	$(\phi +1)\sqrt{2}$	$\frac{3\phi +2}{2}$	$\frac{4\pi }{5}$
Hexacosichore	$\frac{25(2\phi +1)}{4}$	$50\sqrt{2}$	$\phi$	$\frac{(2\phi +1)\sqrt{2}}{2}$	$2\arctan \{(2\phi +1)\sqrt{3}\}$

Représentations

Le tableau suivant recense quelques projections particulières des polychores.

Polychore	Symbole de Schläfli	Diagramme de Coxeter-Dynkin	Polygone de Petrie	Projection orthographique solide	Diagramme de Schlegel	Projection stéréographique
Pentachore	{3,3,3}	Modèle:DCD		Tétraèdre
Tesseract	{4,3,3}	Modèle:DCD		Cube
Hexadécachore	{3,3,4}	Modèle:DCD		Cube
Icositétrachore	{3,4,3}	Modèle:DCD		Cuboctaèdre
Hécatonicosachore	{5,3,3}	Modèle:DCD		Triacontaèdre rhombique tronqué
Hexacosichore	{3,3,5}	Modèle:DCD		Pentaki-icosidodécaèdre

Liste

Pentachore

Un pentachore en rotation.

Le pentachore est le simplexe régulier de dimension 4. Son symbole de Schläfli est {3,3,3}.

Ses autres noms sont : 5-cellules, pentatope, hyperpyramide à base tétraédrique, hypertétraèdre, 4-simplexe.

Ses éléments sont :

• 5 sommets
• 10 arêtes
• 10 faces triangulaires
• 5 cellules tétraédriques

Comme tous les simplexes, il est son propre dual. Il fait partie du groupe de symétrie $A_4$. Sa figure de sommet est un tétraèdre.

Tesseract

Un hypercube en rotation.

C'est un hypercube à 4 dimensions. Son symbole de Schläfli est {4,3,3}.

Ses autres noms sont : l'octachore, le 8-cellules, le 4-cube.

Ses éléments sont :

• 16 sommets
• 32 arêtes
• 24 faces carrées
• 8 cellules cubiques

Son dual est le 16-cellules (un hypercube est en effet toujours dual d'un hyperoctaèdre et vice-versa). Il fait partie du groupe de symétrie $B_4$. Sa figure de sommet est un tétraèdre.

Hexadécachore

Un hexadécachore en rotation.

C'est un hyperoctaèdre à 4 dimensions. Son symbole de Schläfli est {3,3,4}.

Ses autres noms sont : le 16-cellules, le 4-orthoplexe, le 4-octaèdre.

Ses éléments sont :

• 8 sommets
• 24 arêtes
• 32 faces triangulaires
• 16 cellules tétraédriques

Il peut être considéré comme une double hyperpyramide à base octaédrique.

Son dual est le tesseract (un hyperoctaèdre est en effet toujours dual d'un hypercube et vice-versa). Il fait partie du groupe de symétrie $B_4$. Sa figure de sommet est un octaèdre.

Icositétrachore

Un icositétrachore en rotation.

Il n'a aucun analogue en 3 dimensions. Son symbole de Schläfli est {3,4,3}.

Ses autres noms sont : le 24-cellules, l'octaplexe, le poly-octaèdre.

Ses éléments sont :

• 24 sommets
• 96 arêtes
• 96 faces triangulaires
• 24 cellules octaèdriques

Ayant autant de sommets que de cellules, et autant d'arêtes que de faces, il est son propre dual. Il fait partie du groupe de symétrie $F_4$. Sa figure de sommet est un cube.

Hécatonicosachore

Un hécatonicosachore en rotation.

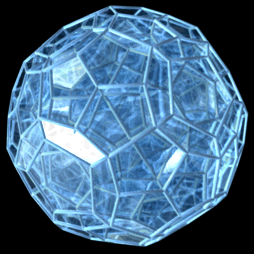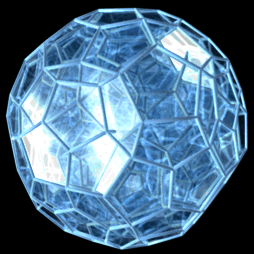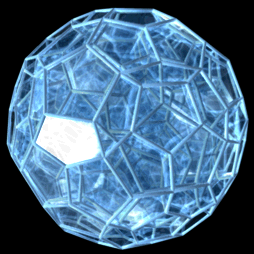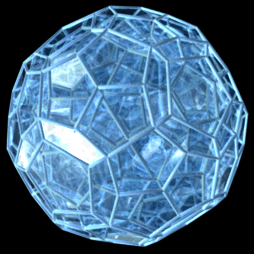
Il est l'analogue quadri-dimensionnel du dodécaèdre régulier. Son symbole de Schläfli est {5,3,3}.

Ses autres noms sont : l'hécatonicosaédroïde, le 120-cellules, le dodécaplexe, l'hyperdodécaèdre, le polydodécaèdre.

Ses éléments sont :

• 600 sommets
• 1200 arêtes
• 720 faces pentagonales
• 120 cellules dodécaèdriques

Son dual est l'hexachosichore, de la même façon que l'icosaèdre était le dual du dodécaèdre. Son groupe de symétrie est $H_4$. Sa figure de sommet est un tétraèdre.

Hexacosichore

Un hexacosichore en rotation.

Il est l'analogue quadri-dimensionnel de l'icosaèdre régulier. Son symbole de Schläfli est {3,3,5}.

Ses autres noms sont : le 600-cellules, le tétraplexe, l'hypericosaèdre, le polytétraèdre.

Ses éléments sont :

• 120 sommets
• 720 arêtes
• 1200 faces triangulaires
• 600 cellules tétraédriques

Son dual est l'hecatonicosachore, de la même façon que le dodécaèdre était le dual de l'icosaèdre. Son groupe de symétrie est $H_4$. Sa figure de sommet est un icosaèdre.

Voir aussi

• Nombre figuré 4-polytopique
• Nombre figuré 4-polytopique centré
• Polychores de Schläfli-Hess, les polychores réguliers non convexes

Liens externes

• Les polychores réguliers sur le site mathcurve
• Les dimensions sur le site dimensions-superieures
• Modèle:MathWorld
• Modèle:En Patrons des polychores réguliers
• Le film documentaire Dimensions donne des moyens de s'imaginer ces objets
• Modèle:En Les polychores réguliers sur Eusebeia
• Modèle:En Alicia Boole Stott’s four-dimension polytopes sur Alicia Boole Stott

• Modèle:Introdugeo
• Modèle:En H. S. M. Coxeter, Regular Polytopes, Modèle:3e éd., Dover Publications, 1973 Modèle:ISBN
• Modèle:En D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions, New York, E. P. Dutton, 1930 (Dover Publications, 1958), chap. X (« The Regular Polytopes »)