Fonction du second degré

Représentation graphique de la fonction $f:x\mapsto x^2-x-2$

En analyse réelle, une fonction du second degré est une fonction numérique définie par Modèle:Indente où $a$, $b$ et $c$ sont des nombres réels qui ne dépendent pas de la variable $x$, avec $a\ne 0$.

Les fonctions polynomiales du second degré sont parfois appelées trinômes du second degré, fonctions quadratiques ou encore fonctions du second degré. Ce sont les fonctions les plus simples, après les fonctions affines.

Ces fonctions du second degré trouvent leurs applications dans des domaines extrêmement variés comme l'étude théorique d'une chute libre en physique.

La représentation graphique d'une fonction du second degré est une parabole qui possède un axe de symétrie parallèle à l'axe des ordonnées. Le signe du nombre a indique le sens de variation de la fonction.

Différentes formes

Toute expression algébrique admet une infinité d'écritures. Pour une fonction du second degré, trois d'entre elles sont particulièrement intéressantes.

Forme développée

La forme développée, réduite et ordonnée d'une fonction du second degré est celle qui est donnée en introduction de cet article et dans les livres en général :

$f(x)=a{x}^2+bx+c$

avec Modèle:Mvar non nul.

Dans ce cas, les nombres $a$, $b$ et $c$, suivant le vocabulaire des polynômes, sont respectivement appelés coefficients du second degré, du premier degré et terme constant. Les termes $a{x}^2$, $bx$ et $c$ sont les monômes respectivement de degré 2, 1 et 0. Sous cette forme constituée de trois monômes, la fonction est souvent appelée trinôme du second degré.

Forme canonique

Toute fonction du second degré possède une forme réduite ou forme canonique, où la variable Modèle:Mvar n'apparaît qu'une seule fois. Chacune des deux expressions suivantes peut être nommée forme canonique, ces expressions ne diffèrent que par une factorisation par Modèle:Mvar : Modèle:Retrait Modèle:Retrait

Les nombres $-\frac{b}{2a}$ et $f(-\frac{b}{2a})=-\frac{b^2-4ac}{4a}$ correspondent respectivement à l’abscisse et l'ordonnée du sommet de la parabole représentative du trinôme. Le nombre $b^2-4ac$, quant à lui, est appelé discriminant et souvent noté $\mathrm{\Delta }$.

En effet, on factorise d'abord l'expression par a : Modèle:Retrait

En appliquant la première identité remarquable, on a : Modèle:Retrait

Les formes canoniques sont particulièrement intéressantes car elles permettent d'écrire la fonction du second degré comme une composée de fonctions affines avec la fonction carré. La plupart des résultats sur la fonction (variations, symétrie, signe…) se démontrent grâce à l'une ou l'autre des formes canoniques.

Forme factorisée

Une fonction du second degré peut parfois s'écrire sous une des formes factorisées suivantes :

• $f(x)=a(x-r_1)(x-r_2)$ si et seulement si le discriminant ∆ vu à la section précédente est strictement positif, avec $r_1=\frac{-b-\sqrt{\mathrm{\Delta }}}{2a}$, $r_2=\frac{-b+\sqrt{\mathrm{\Delta }}}{2a}$ ;
• $f(x)=a(x-r_0{)}^2$ si et seulement si ∆ est nul, avec $r_0=\alpha =-\frac{b}{2a}$ ;
• Si le discriminant est négatif, la fonction n'est pas factorisable dans ℝ.

En effet, si l’on part de la forme canonique $a[{(x+\frac{b}{2a})}^2-\frac{b^2-4ac}{4a^2}]=a[{(x+\frac{b}{2a})}^2-\frac{\mathrm{\Delta }}{(2a{)}^2}]$, on obtient

• pour Δ strictement positif, en appliquant la troisième identité remarquable : Modèle:Retrait Modèle:Retrait
• et pour Δ nul, directement Modèle:Retrait

La forme factorisée est intéressante car elle permet, par l’application du théorème de l'équation produit-nul de résoudre l'équation f(x) = 0 sur ℝ ou ℂ, ou par l’application de la règle des signes de dresser un tableau de signes de f sur ℝ, donc de résoudre une inéquation du second degré.

Équation et inéquation du second degré

Modèle:Article détaillé Une équation du second degré est une équation équivalente à $f(x)=0$, où $f$ est une fonction du second degré. De même, une inéquation du second degré est une inéquation équivalente à l'une des quatre formes : $f(x)⩽0$, $f(x)<0$, $f(x)⩾0$ ou $f(x)>0$, $f$ désignant toujours une fonction du second degré.

On dit qu'un nombre $r$ est une racine de l'équation et de $f$ si $f(r)=0$.

Équation

On démontre, par application du théorème de l’équation produit-nul sur la forme factorisée, que

• si $\mathrm{\Delta }>0$ alors $f$ possède deux racines qui sont $r_1=\frac{-b-\sqrt{\mathrm{\Delta }}}{2a}$ et $r_2=\frac{-b+\sqrt{\mathrm{\Delta }}}{2a}$ ;
• si $\mathrm{\Delta }=0$ alors $f$ possède une racine double qui est $r_0=\frac{-b}{2a}$ ;
• si $\mathrm{\Delta }<0$ alors $f$ ne possède pas de racine dans l'ensemble $ℝ$ mais il en possède dans l'ensemble $ℂ$ : $\frac{-b+i\sqrt{|\mathrm{\Delta }|}}{2a}$ et $\frac{-b-i\sqrt{|\mathrm{\Delta }|}}{2a}$, où $i$ désigne l’unité imaginaire.

Opérations sur les racines

Si le polynôme du second degré possède deux racines $r_1$ et $r_2$ (éventuellement confondues), il admet comme forme factorisée $a(x-r_1)(x-r_2)$. Par développement de cette forme et identification des termes de même degré avec la forme développée, on obtient les égalités : Modèle:Retrait et Modèle:Retrait Ces égalités sont notamment utiles en calcul mental et en cas de « racine évidente ». Par exemple, si on sait qu'une racine est égale à 1, l'autre sera $\frac{c}{a}$.

Inéquation

Le signe d'une fonction du second degré se déduit de la forme canonique qui, en posant $\mathrm{\Delta }=b^2-4ac$, s'écrit : Modèle:Retrait

Si Modèle:Math, alors, pour tout réel Modèle:Mvar, $\frac{-\mathrm{\Delta }}{4a^2}>0$ et d'autre part ${(x+\frac{b}{2a})}^2⩾0$ comme carré de nombre réel. Donc Modèle:Math est toujours du signe de Modèle:Mvar.

Si Modèle:Math, la situation est quasiment la même, sauf que la fonction du second degré s'annule une fois, pour $x=\frac{-b}{2a}$.

Si Modèle:Math, la forme canonique s'écrit comme une différence de deux carrés, en remarquant que le nombre positif $\frac{\mathrm{\Delta }}{4a^2}$ s'écrit ${\left(\frac{\sqrt{\mathrm{\Delta }}}{2a}\right)}^2$. Elle peut donc se factoriser suivant l'identité remarquable Modèle:Math et admet deux racines. La fonction du second degré est alors du signe opposé à celui de Modèle:Mvar entre les racines et du signe de Modèle:Mvar ailleurs.

Tous ces résultats donnent six cas possibles illustrés dans la partie représentation graphique de cet article et qui se résument en une seule phrase : Modèle:Théorème

	Modèle:Math	Modèle:Math
Modèle:Math	$\begin{array}{cccc}x& -\mathrm{\infty }& & +\mathrm{\infty }\\ f(x)& & -& \end{array}$	$\begin{array}{cccc}x& -\mathrm{\infty }& & +\mathrm{\infty }\\ f(x)& & +& \end{array}$
Modèle:Math	$\begin{array}{cccccc}x& -\mathrm{\infty }& & \frac{-b}{2a}& & +\mathrm{\infty }\\ f(x)& & -& 0& -& \end{array}$	$\begin{array}{cccccc}x& -\mathrm{\infty }& & \frac{-b}{2a}& & +\mathrm{\infty }\\ f(x)& & +& 0& +& \end{array}$
Modèle:Math	$\begin{array}{cccccccc}x& -\mathrm{\infty }& & r_1& & r_2& & +\mathrm{\infty }\\ f(x)& & -& 0& +& 0& -& \end{array}$	$\begin{array}{cccccccc}x& -\mathrm{\infty }& & r_1& & r_2& & +\mathrm{\infty }\\ f(x)& & +& 0& -& 0& +& \end{array}$

Représentation graphique

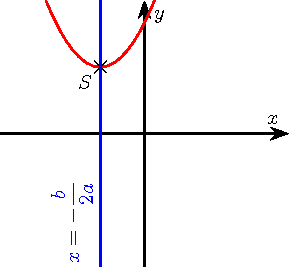
Modèle:Article connexe La représentation graphique d'une fonction du second degré est une parabole qui admet comme axe de symétrie la droite d'équation $x=\frac{-b}{2a}$. La réciproque est en partie vraie : quelle que soit une parabole donnée, il est possible de choisir un repère orthonormé du plan pour lequel il existe une fonction du second degré dont la parabole est le graphe.

Les variations et la forme de la parabole présentent deux cas, suivant le signe du coefficient de second degré Modèle:Mvar.

Si Modèle:Mvar est positif

La parabole admet un minimum ; la fonction est décroissante sur l'intervalle $]-\mathrm{\infty },\frac{-b}{2a}]$ puis croissante. Les coordonnées du minimum sont $(\frac{-b}{2a},c-\frac{b^2}{4a})$.

La parabole est tournée « vers le haut » : pour tous points A et B appartenant à la parabole, le segment [AB] est situé au-dessus de cette courbe. Une fonction répondant à ces propriétés est dite convexe.

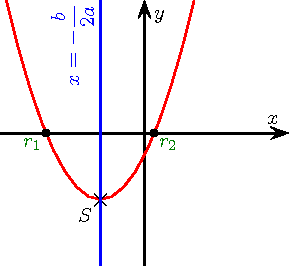
Si Modèle:Mvar est négatif

La parabole admet un maximum et les variations de la fonction sont inversées par rapport au cas précédent : d'abord croissante, puis décroissante. Les coordonnées du maximum sont aussi $M(\frac{-b}{2a};c-\frac{b^2}{4a})$.

La parabole est tournée « vers le bas ». La fonction est dite concave.

Fonctions de la forme Modèle:Math pour Modèle:Mvar égal à 0,1 ; 0,3 ; 1 et 3. Plus Modèle:Mvar est loin de zéro, plus la parabole est élancée.

La valeur absolue du nombre Modèle:Mvar donne également la vitesse de variation de la fonction du second degré. Ainsi, plus Modèle:Mvar est proche de zéro, plus la parabole va paraître « aplatie », pour un repère donné.

Pour l'intersection de la parabole avec l'axe des abscisses, un autre nombre joue un rôle central, le discriminant, souvent noté ∆ et égal à Modèle:Math. La parabole n'a aucun point d'intersection avec l'axe des abscisses lorsque ∆ < 0, est tangente en un point avec cet axe lorsque ∆ = 0 et possède deux points d'intersection lorsque ∆ > 0.

Ces résultats peuvent être interprétés en termes d'équations ou d'inéquations et se démontrent à l'aide de calculs algébriques, éventuellement complétés par des raisonnements d'analyse mathématique (avec utilisation de la dérivée de la fonction) et de géométrie (voir plus bas).

	$a>0$	$a<0$
$\mathrm{\Delta }<0$
$\mathrm{\Delta }=0$
$\mathrm{\Delta }>0$

Analyse

Toute fonction du second degré est continue, ce qui signifie qu'elle n'admet pas de « cassure » : à une variation infinitésimale de la variable x correspond une variation infinitésimale de la fonction, pour tout nombre réel x.

De plus, elle est indéfiniment dérivable : toute fonction f de la forme $f(x)=a{x}^2+bx+c$ admet

• une dérivée $f{}^{\prime }(x)=2ax+b$ ;
• une dérivée seconde (dérivée de la dérivée) $f{}^{″}(x)=2a$ ;
• des dérivées successives (dérivée troisième, quatrième, etc.) toutes nulles.

Du point de vue de leurs variations, les fonctions du second degré peuvent être classées en deux groupes, suivant le signe du coefficient de second degré $a$ :

• Si $a>0$, la fonction est strictement décroissante puis strictement croissante et atteint son minimum en $\frac{-b}{2a}$ ;
• Si $a<0$, la fonction est strictement croissante puis strictement décroissante et atteint son maximum en $\frac{-b}{2a}$.

Dans les deux cas, les coordonnées de l'extremum sont donc $(\frac{-b}{2a},c-\frac{b^2}{4a})$.

Ce résultat peut être démontré par l'étude du signe de la dérivée de $f$, en utilisant le fait qu'une fonction dérivable est strictement croissante sur tout intervalle où sa dérivée est strictement positive et strictement décroissante sur tout intervalle où sa dérivée est strictement négative. La convexité de $f$ (ou sa concavité lorsque $a<0$) se démontre également par les dérivées. En effet, toute fonction dont la dérivée seconde est positive est convexe, et toute fonction dont la dérivée seconde est négative est concave.

Les primitives de la fonction $f(x)=a{x}^2+bx+c$ sont les fonctions du troisième degré de la forme $G_k(x)=\frac{1}{3}a{x}^3+\frac{1}{2}b{x}^2+cx+k$, où $k$ est une constante. Ce résultat se démontre par application des règles de calcul sur les dérivées ou primitives, ou par la méthode de la quadrature de la parabole qui mêle géométrie et passage à la limite.

Historique

Les calculs fondamentaux sur les fonctions du second degré ont une histoire sensiblement identique à celle des équations du second degré, qui est très ancienne (la tablette d'argile BM 13901 qui leur est en partie consacrée date du [[XVIIIe siècle av. J.-C.|Modèle:XVIIIe siècle av. J.-C]] !). Leur étude, en qualité de fonction, est beaucoup plus récente puisque le concept de fonction est a été introduit par Leibniz à la fin du Modèle:XVIIe siècle. Modèle:…

Voir aussi

Articles connexes

• Équation cubique
• Équation quartique

Bibliographie

Manuels de seconde et première dans les lycées en France

Modèle:Palette Modèle:Portail