Méthodes de calcul d'intégrales de contour

En analyse complexe, lModèle:'intégration de contour est une technique de calcul d'intégrale le long de chemins sur le plan complexeModèle:,Modèle:,

L'intégration de contour est fortement liée au calculs de résidus, une méthode de calcul utilisée pour évaluer des intégrales curvilignes sur l'axe des réelles, que les outils de la théorie de l'intégration ne permettent pas de calculer par une simple analyse réelle

Les méthodes d'intégration de contour incluent :

• l'intégration directe d'une fonction à valeurs complexes le long d'une courbe du plan complexe (ledit contour) ;
• une application de la formule intégrale de Cauchy ;
• l'application du théorème des résidus.

Ces méthodes peuvent être combinées pour obtenir les résultats attendus.

Courbes dans le plan complexe

Les contours donnent une définition précise des courbes sur lesquelles une intégrale peut être exactement définie. Une courbe du plan complexe est donc une fonction continue renvoyant un intervalle réel fermé sur le plan complexe : Modèle:Math.

Cette définition coïncide avec la notion intuitive d'une courbe, mais inclut une paramétrisation par une fonction continue à partir d'un intervalle fermé. Cette définition plus précise permet de réfléchir aux propriétés que doit avoir une courbe pour qu'elle soit utile à l'intégration. Dans les sous-sections suivantes, on réduira l'ensemble de courbes intégrables pour n'inclure que celles qui peuvent être construites à partir d'un nombre fini de courbes continues, auxquelles on peut donner une direction. De plus, on empêchera les "morceaux" de se croiser, et on imposera que chaque morceau ait une dérivée continue finie (non nulle). Ces exigences permettent de ne considérer que les courbes qui peuvent être tracées, comme par un stylo, dans une séquence de traits constants et réguliers, qui ne s'arrêtent que pour commencer un nouveau morceau de la courbe, le tout sans relever le stylo.

Courbes lisses orientées

Les contours sont définis comme des courbes régulières orientées. On peut ainsi définir précisément un "morceau" d'une courbe lisse, dont on trace un contour.

Une courbe lisse est une fonction Modèle:Math avec une dérivée continue qui ne s'annule pas et ne possèdent pas de point double, sauf peut-être aux extrémités (tel que Modèle:Math). On parle alors de courbe fermée, et la fonction doit alors être bijective et les dérivées doivent correspondre aux extrémités (Modèle:Math). Sinon, on parle d'arc lisse ou de courbe ouverte.

La paramétrisation d'une courbe donne un ordre naturel des points de la courbe : Modèle:Math est avant Modèle:Math si Modèle:Math. On peut ainsi définir une courbe lisse orientée, ce qui est surtout utile pour les courbes indépendantes d'une paramétrisation spécifique. Ceci peut être fait en considérant des classes d'équivalence de courbes lisses avec la même direction. Une courbe lisse orientée est alors un ensemble ordonné de points du plan complexe, image d'une courbe lisse dans leur ordre naturel (selon la paramétrisation). Il faut noter que tous les ordres de points correspondent à l'ordre naturel d'une courbe lisse. En effet, une courbe lisse donnée n'a que deux ordres. De plus, une courbe fermée peut avoir tout point comme extrémité, alors qu'un arc lisse aura deux possibilités.

Contours

Les contours sont les classes de courbes sur lesquelles on peut définir l'intégration de contour. Un contour est une courbe orientée qui est formé d'une suite finie de courbes lisses dirigées dont les extrémités sont reliées pour donner une seule direction. Cela nécessite que la suite de courbes Modèle:Math soit telle que, le point final de Modèle:Math coïncide avec le point initial de Modèle:Math, Modèle:Math. Cela inclut toutes les courbes lisses dirigées. De même, un point singleton du plan complexe peut être considéré comme un contour. Le symbole + est souvent utilisé pour désigner le raccordement des courbes afin de former une nouvelle courbe. Ainsi on peut construire un contour Modèle:Math qui est formé de Modèle:Mvar courbes telles que $$\mathrm{\Gamma }={\gamma }_1+{\gamma }_2+\cdots +{\gamma }_n.$$

Intégrales de contour

L'intégrale de contour d'une fonction complexe Modèle:Math, est une généralisation de l'intégrale pour les fonctions réelles. Pour les fonctions continues du plan complexe, l'intégrale de contour peut être définie de façon analogue à l'intégrale curviligne en définissant d'abord l'intégrale le long d'une courbe lisse orientée en termes d'intégrales sur un paramètre réel. Une définition plus générale peut être donnée en termes de partitions du contour par analogie avec la partition d'un intervalle et l'intégrale de Riemann. Dans les deux cas, l'intégrale sur un contour est définie comme la somme des intégrales sur les courbes lisses orientées qui constituent le contour.

Pour les fonctions continues

Pour définir l'intégrale de contour dans ce cas, on dit d'abord considérer l'intégrale, sur une variable réelle, d'une fonction à valeurs complexes. Soit Modèle:Math une fonction à valeurs complexes d'une variable réelle Modèle:Mvar. Les parties réelles et imaginaires de Modèle:Mvar sont souvent dénotées Modèle:Math et Modèle:Math, respectivement, de sorte que $$f(t)=u(t)+\mathrm{i}v(t).$$ Alors l'intégrale de Modèle:Mvar sur l'intervalle Modèle:Math est donnée par $$\begin{array}{cc}\underset{a}{\overset{b}{\int }}f(t)\mathrm{d}t& =\underset{a}{\overset{b}{\int }}(u(t)+\mathrm{i}v(t))\mathrm{d}t\\ & =\underset{a}{\overset{b}{\int }}u(t)\mathrm{d}t+\mathrm{i}\underset{a}{\overset{b}{\int }}v(t)\mathrm{d}t.\end{array}$$

Soit Modèle:Math une fonction continue sur une courbe lisse orientée Modèle:Mvar. Soit Modèle:Math une paramétrisation de Modèle:Mvar consistante avec sa direction. Alors l'intégrale le long de Modèle:Mvar est notée $$\underset{\gamma }{\int }f(z)\mathrm{d}z$$ et se calcule par $$\underset{\gamma }{\int }f(z)\mathrm{d}z=\underset{a}{\overset{b}{\int }}f(\gamma (t)){\gamma }^{\prime }(t)\mathrm{d}t.$$

Cette définition est bien définie. Ainsi, le résultat est indépendant de la paramétrisation choisie. Dans le cas où l'intégrale à droite n'existe pas, l'intégrale le long de Modèle:Mvar n'est pas définie.

Comme une généralisation de l'intégrale de Riemann

La généralisation de l'intégrale de Riemann aux fonctions d'une variable complexe est faite par analogie avec les fonctions d'une variable réelle. La partition d'une courbe lisse orientée Modèle:Mvar est définie comme un ensemble de points ordonnés et fini sur Modèle:Mvar. L'intégrale sur la courbe est la limite des sommes finies de valeurs de fonction, prise aux points de la partition, où la limite est celle où la distance maximum entre n'importe lequel des deux points successifs sur la partition (dans le plan complexe 2D), connu comme le maillage, tend vers zéro.

Exemples de contours particuliers

Arc de Jordan

Un arc de Jordan est une courbe fermée simple du plan complexe qui sépare le plan en deux parties : l'intérieur et l'extérieur. Les contours les plus simples et intuitifs pour les intégrales de contour sont les arcs de Jordan et les lacets. Afin de pouvoir appliquer le théorème des résidus, on construira donc un lacet entourant les pôles de l'intégrande.

Contour de Hankel

Un contour de Hankel, parcouru dans le sens positif.

Une version totalement linéaire du contour de Hankel.

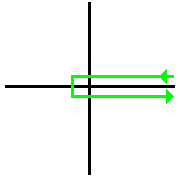
Un contour de Hankel est une courbe ouverte entourant un demi-axe du plan.

La version la plus courante consiste en deux demi-droites parallèles au demi-axe choisi, reliées par un arc de cercle centré à l'origine du demi-axe. Il est parcouru dans le sens horaire.

Ce type de contour est utilisé lorsqu'un logarithme complexe est impliqué, comme la fonction Gamma d'Euler sur le plan complexe. Modèle:Clr

Contour de Pochhamer

Un contour de Pochhammer tourne dans le sens horaire autour d'un point, puis dans le sens horaire autour d'un autre point, puis dans le sens anti-horaire autour du premier point, et enfin dans le sens anti-horaire autour du second point. La position exacte, la courbure, etc. ne sont pas essentielles dans ce cas, seule la suite de tours importe.

Un contour de Pochhammer, introduit par Camille Jordan et Leo Pochhammer, est utile pour les intégrales de contour autour de deux points. En notant Modèle:Mvar et Modèle:Mvar les boucles parcourues autour des points Modèle:Mvar et Modèle:Mvar respectivement, alors le contour de Pochhammer est Modèle:Math, où l'exposant −1 désigne un chemin parcouru dans le sens inverse.

Par sa construction, la courbe est homologue à 0 mais pas homotopique à 0. Son indice autour de tout point est de 0 malgré le fait qu'à l'intérieur le plan doublement épointé il ne peut pas être réduit à un seul point.

Un cycle de Pochhammer est homologue à zero : c'est la frontière de la surface verte moins la frontière de la rouge.

Méthodes directes

Les méthodes directes impliquent le calcul de l'intégrale par des méthodes similaires aux calculs d'intégrales curvilignes en calcul multivarié. Ainsi, on utilise la méthode suivante :

• paramétrer le contour

  le contour est paramétré par une fonction de variables réelles à valeurs complexes différentiable, ou en morceaux paramétrables

• substitution de la paramétrisation dans l'intégrande

  substituer la paramétrisation dans l'intégrande permet de revenir à des intégrales de la variable réelle

• évaluation directe

Exemple

Un résultat fondamental en analyse complexe est que l'intégrale de contour de Modèle:Math vaut Modèle:Math, avec un chemin pris sur le cercle unité dans le sens anti-horaire (ou toute courbe de Jordan orientée positivement autour de 0). Dans le cas du cercle unité, il y a une méthode directe de calcul de l'intégrale $${\oint }_C\frac{1}{z}\mathrm{d}z.$$

Dans le calcul de cette intégrale, le cercle unité est caractérisé par Modèle:Math, qu'on paramètre par Modèle:Math, avec Modèle:Math, ce qui donne Modèle:Math, d'où $${\oint }_C\frac{1}{z}\mathrm{d}z=\underset{0}{\overset{2\pi }{\int }}\frac{1}{{\mathrm{e}}^{\mathrm{i}t}}{\mathrm{i}\mathrm{e}}^{\mathrm{i}t}\mathrm{d}t=\mathrm{i}\underset{0}{\overset{2\pi }{\int }}1\mathrm{d}t=\mathrm{i}t{|}_0^{2\pi }=(2\pi -0)\mathrm{i}=2\pi \mathrm{i}.$$

On retrouve bien la valeur attendue.

Applications de théorèmes intégraux

Les théorèmes intégraux sont souvent utilisés les intégrales de contour sur un chemin, en utilisant le fait que l'intégrale d'une variable réelle est calculée en même temps que le calcul sur le chemin dans le plan complexe.

On utilise notamment la formule intégrale de Cauchy ou le théorème des résidus, de la façon suivante :

• un contour spécifique est choisi :

  le contour est choisi de façon à contenir la partie du plan complexe correspondant à l'intégrale réelle, et entourer les singularités de l'intégrande de sorte que le théorème s'applique

• application du théorème intégral de Cauchy

  l'intégrale est réduite à une intégration autour d'un petit cercle autour de chaque pole

• application du théorème intégral de Cauchy ou théorème des résidus

  l'application donne alors une valeur le long du contour

• division du contour en un contour sur les parties réelle et imaginaire

  l'entièreté du contour peut être divisée en un contour suivant la partie du plan complexe qui décrit l'intégrale réelle telle que choisie auparavant (on la note Modèle:Mvar), et la partie qui traverse le plan complexe (on la note Modèle:Mvar). L'intégrale sur le contour entier est la somme des intégrales sur ces deux contours.

• démonstration que l'intégrale passant par le plan complexe n'a aucun rôle dans la somme

  si l'intégrale sur Modèle:Mvar peut être réduite à 0, ou si l'intégrale réelle s'avère impropre, alors si on prouve que l'intégrale sur Modèle:Mvar tend vers 0, l'intégrale sur Modèle:Mvar va tendre vers l'intégrale sur Modèle:Math.

• conclusion

  si le point suivant est vérifié, alors on peut calculer directement Modèle:Mvar, l'intégrale réelle.

Exemple 1

Illustration du chemin utilisé dans l'exemple.

On considère l'intégrale $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{1}{{(x^2+1)}^2}\mathrm{d}x,$$

Pour le calcul, on passe par la fonction d'une variable complexe $$f(z)=\frac{1}{{(z^2+1)}^2}$$

qui présente deux singularités en Modèle:Math et Modèle:Math. On choisit donc un contour qui contient l'intégrale réelle, par exemple un demi-cercle dont le diamètre est formé par un intervalle sur la droite réelle (allant de Modèle:Math vers Modèle:Mvar, pour Modèle:Mvar réel strictement supérieur à 1) conviendrait. On note ce contour Modèle:Mvar.

Il y a deux façons de procéder, selon le théorème qu'on souhaite utiliser :

Avec la formule intégrale de Cauchy

On note que : $${\oint }_{C}f(z)\mathrm{d}z=\underset{-a}{\overset{a}{\int }}f(z)\mathrm{d}z+\underset{\text{Arc}}{\int }f(z)\mathrm{d}z$$ soit $$\underset{-a}{\overset{a}{\int }}f(z)\mathrm{d}z={\oint }_{C}f(z)\mathrm{d}z-\underset{\text{Arc}}{\int }f(z)\mathrm{d}z.$$

On observe que $$f(z)=\frac{1}{{(z^2+1)}^2}=\frac{1}{(z+\mathrm{i}{)}^2(z-\mathrm{i}{)}^2}.$$

Comme la seule singularité contenue dans le contour est celle en Modèle:Math, on peut écrire $$f(z)=\frac{\frac{1}{(z+\mathrm{i}{)}^2}}{(z-\mathrm{i}{)}^2},$$ ce qui donne la fonction sous une forme qui permet l'application directe de la formule intégrale de Cauchy : $${\oint }_{C}f(z)\mathrm{d}z={\oint }_C\frac{\frac{1}{(z+\mathrm{i}{)}^2}}{(z-\mathrm{i}{)}^2}\mathrm{d}z=2\pi \mathrm{i}{\frac{\mathrm{d}}{\mathrm{d}z}\frac{1}{(z+\mathrm{i}{)}^2}|}_{z=\mathrm{i}}=2\pi \mathrm{i}{\left[\frac{-2}{(z+\mathrm{i}{)}^3}\right]}_{z=\mathrm{i}}=\frac{\pi }{2}$$

On prend la dérivée première, dans les calculs précédents, car le pole est d'ordre 2. Ainsi, Modèle:Math est prise au carré, donc on utilise a dérivée première de Modèle:Math. Si on avait Modèle:Math élevé au cube, on aurait utilisé la dérivée seconde et divisé par 2!, etc. Le cas de Modèle:Math à la puissance 1 correspond à une dérivée d'ordre 0 — soit Modèle:Math elle-même.

On doit montrer que l'intégrale sur le demi-cercle tend vers zéro pour Modèle:Math, par le lemme d'estimation $$|\underset{\text{Arc}}{\int }f(z)\mathrm{d}z|\le L(\text{Arc})M$$

avec Modèle:Mvar un majorant de Modèle:Math sur l'arc et Modèle:Mvar désignant la longueur de l'arc. Ainsi, $$|\underset{\text{Arc}}{\int }f(z)\mathrm{d}z|\le \frac{a\pi }{{(a^2-1)}^2}{⟶}_{a\to \mathrm{\infty }}0.$$ Ainsi $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{1}{{(x^2+1)}^2}\mathrm{d}x=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}f(z)\mathrm{d}z=\underset{a\to +\mathrm{\infty }}{\lim }\underset{-a}{\overset{a}{\int }}f(z)\mathrm{d}z=\frac{\pi }{2}.◻$$

Par le théorème des résidus

On considère la série de Laurent de Modèle:Math en Modèle:Math, qui est la seule singularité à considérer. On a $$f(z)=\frac{-1}{4(z-\mathrm{i}{)}^2}+\frac{-\mathrm{i}}{4(z-\mathrm{i})}+\frac{3}{16}+\frac{\mathrm{i}}{8}(z-\mathrm{i})+\frac{-5}{64}(z-\mathrm{i}{)}^2+\cdots$$

Il est clair par l'observation que le résidu vaut Modèle:Math, ainsi, la formule des résidus permet de conclure : $${\oint }_{C}f(z)\mathrm{d}z={\oint }_C\frac{1}{{(z^2+1)}^2}\mathrm{d}z=2\pi \mathrm{i}{\mathrm{Res}}_{z=\mathrm{i}}f(z)=2\pi \mathrm{i}(-\frac{\mathrm{i}}{4})=\frac{\pi }{2}◻$$

Remarque sur le contour

On aurait pu choisir le demi-cercle dans la partie inférieure du plan complexe, qui entoure la singularité en Modèle:Math. Pour avoir l'intégrale sur l'axe réel bien orienté, il faudrait parcourir le demi-cercle dans le sens horaire, ce qui change le signe de l'intégrale complète, mais pas le résultat final sur l'intégrale réelle.

Exemple 2 – Distribution de Cauchy

L'intégrale $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{{\mathrm{e}}^{\mathrm{i}tx}}{x^2+1}\mathrm{d}x$$

Le contour

(qui apparait en théorie des probabilités comme un multiple scalaire de la fonction caractéristique de la loi de Cauchy) résiste aux techniques d'analyse élémentaire. On l'évalue en l'exprimant comme la limite d'intégrales de contour faites sur les demi-cercles dont le diamètre est formé par l'intervalle de la droite réelle entre Modèle:Math et Modèle:Mvar et sur le demi-cercle centré en 0 et de rayon Modèle:Mvar, sur le demi-plan complexe des nombres de partie imaginaire positives, parcouru dans le sens anti-horaire. On prendra Modèle:Mvar plus grand que 1, de façon que l'affixe de Modèle:Math soit à l'intérieur de la courbe. L'intégrale de contour devient alors $$\underset{C}{\int }\frac{{\mathrm{e}}^{\mathrm{i}tz}}{z^2+1}\mathrm{d}z.$$

Comme Modèle:Math est une fonction entière (sans singularité sur le plan complexe), l'intégrande a des singularités aux lieux où le dénominateur Modèle:Math s'annule. La factorisation donne Modèle:Math, les singularités sont en Modèle:Math ou Modèle:Math. Seul un de ces points est dans la zone délimitée par le contour. Le résidu de Modèle:Math en Modèle:Math est $$\underset{z\to \mathrm{i}}{\lim }(z-\mathrm{i})f(z)=\underset{z\to \mathrm{i}}{\lim }(z-\mathrm{i})\frac{{\mathrm{e}}^{\mathrm{i}tz}}{z^2+1}=\underset{z\to \mathrm{i}}{\lim }(z-\mathrm{i})\frac{{\mathrm{e}}^{\mathrm{i}tz}}{(z-\mathrm{i})(z+\mathrm{i})}=\underset{z\to \mathrm{i}}{\lim }\frac{{\mathrm{e}}^{\mathrm{i}tz}}{z+\mathrm{i}}=\frac{{\mathrm{e}}^{-t}}{2\mathrm{i}}.$$

Selon le théorème des résidus, on a alors $$\underset{C}{\int }f(z)\mathrm{d}z=2\pi \mathrm{i}{\mathrm{Res}}_{z=\mathrm{i}}f(z)=2\pi \mathrm{i}\frac{{\mathrm{e}}^{-t}}{2\mathrm{i}}=\pi {\mathrm{e}}^{-t}.$$

Le contour Modèle:Mvar peut être séparé en une partie "droite" et un arc, donc $$\underset{\text{droite}}{\int }+\underset{\text{arc}}{\int }=\pi {\mathrm{e}}^{-t},$$ est donc $$\underset{-a}{\overset{a}{\int }}=\pi {\mathrm{e}}^{-t}-\underset{\text{arc}}{\int }.$$

Selon le lemme de Jordan, si Modèle:Math alors $$\underset{\text{arc}}{\int }\frac{{\mathrm{e}}^{\mathrm{i}tz}}{z^2+1}\mathrm{d}z\to 0\text{ pour }a\to \mathrm{\infty }.$$

Ainsi, si Modèle:Math alors $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{{\mathrm{e}}^{\mathrm{i}tx}}{x^2+1}\mathrm{d}x=\pi {\mathrm{e}}^{-t}.$$

Un argument similaire avec un arc qui tourne autour de Modèle:Math au lieu de Modèle:Math montre que si Modèle:Math alors $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{{\mathrm{e}}^{\mathrm{i}tx}}{x^2+1}\mathrm{d}x=\pi {\mathrm{e}}^t,$$ ainsi, on obtient: $$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{{\mathrm{e}}^{\mathrm{i}tx}}{x^2+1}\mathrm{d}x=\pi {\mathrm{e}}^{-|t|}.◻$$

(Si Modèle:Math alors l'intégrale peut être calculée grâce à l'analyse réelle et vaut Modèle:Math.)

Exemple 3 – intégrales trigonométriques

Certaines substitutions peuvent être aux intégrales impliquant des fonctions trigonométriques, ainsi l'intégrande est transformé en une fonction rationnelle d'une variable complexe et on peut appliquer les méthodes vues au-dessus pour calculer l'intégrale. On peut considérer par exemple $$\underset{-\pi }{\overset{\pi }{\int }}\frac{1}{1+3(\cos t{)}^2}\mathrm{d}t.$$

On veut faire une substitution de Modèle:Math. On applique la formule d'Euler $$\cos t=\frac{1}{2}({\mathrm{e}}^{\mathrm{i}t}+{\mathrm{e}}^{-\mathrm{i}t})=\frac{1}{2}(z+\frac{1}{z})$$ et donc $$\frac{\mathrm{d}z}{\mathrm{d}t}=\mathrm{i}z,\mathrm{d}t=\frac{\mathrm{d}z}{\mathrm{i}z}.$$

On considère Modèle:Mvar le cercle unité, ce qui donne par substitution : $$\begin{array}{cc}{\oint }_C\frac{1}{1+3{\left(\frac{1}{2}(z+\frac{1}{z})\right)}^2}\frac{\mathrm{d}z}{\mathrm{i}z}& ={\oint }_C\frac{1}{1+\frac{3}{4}{(z+\frac{1}{z})}^2}\frac{1}{\mathrm{i}z}\mathrm{d}z\\ & ={\oint }_C\frac{-\mathrm{i}}{z+\frac{3}{4}z{(z+\frac{1}{z})}^2}\mathrm{d}z\\ & =-\mathrm{i}{\oint }_C\frac{\mathrm{d}z}{z+\frac{3}{4}z(z^2+2+\frac{1}{z^2})}\\ & =-\mathrm{i}{\oint }_C\frac{\mathrm{d}z}{z+\frac{3}{4}(z^3+2z+\frac{1}{z})}\\ & =-\mathrm{i}{\oint }_C\frac{\mathrm{d}z}{\frac{3}{4}{z}^3+\frac{5}{2}z+\frac{3}{4z}}\\ & =-\mathrm{i}{\oint }_C\frac{4}{3z^3+10z+\frac{3}{z}}\mathrm{d}z\\ & =-4\mathrm{i}{\oint }_C\frac{\mathrm{d}z}{3z^3+10z+\frac{3}{z}}\\ & =-4\mathrm{i}{\oint }_C\frac{z}{3z^4+10z^2+3}\mathrm{d}z\\ & =-4\mathrm{i}{\oint }_C\frac{z}{3(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z+\frac{\mathrm{i}}{\sqrt{3}})(z-\frac{\mathrm{i}}{\sqrt{3}})}\mathrm{d}z\\ & =-\frac{4\mathrm{i}}{3}{\oint }_C\frac{z}{(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z+\frac{\mathrm{i}}{\sqrt{3}})(z-\frac{\mathrm{i}}{\sqrt{3}})}\mathrm{d}z.\end{array}$$

Les singularités à considérer sont en $\frac{\pm \mathrm{i}}{\sqrt{3}}.$ Soit Modèle:Math un petit cercle autour de $\frac{\mathrm{i}}{\sqrt{3}},$ et Modèle:Math un petit cercle autour de $\frac{-\mathrm{i}}{\sqrt{3}}.$ On en déduit : $$\begin{array}{cc}& -\frac{4\mathrm{i}}{3}[{\oint }_{C_1}\frac{\frac{z}{(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z+\frac{\mathrm{i}}{\sqrt{3}})}}{z-\frac{\mathrm{i}}{\sqrt{3}}}\mathrm{d}z+{\oint }_{C_2}\frac{\frac{z}{(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z-\frac{\mathrm{i}}{\sqrt{3}})}}{z+\frac{\mathrm{i}}{\sqrt{3}}}\mathrm{d}z]\\ =& -\frac{4\mathrm{i}}{3}[2\pi \mathrm{i}{\left[\frac{z}{(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z+\frac{\mathrm{i}}{\sqrt{3}})}\right]}_{z=\frac{\mathrm{i}}{\sqrt{3}}}+2\pi \mathrm{i}{\left[\frac{z}{(z+\mathrm{i}\sqrt{3})(z-\mathrm{i}\sqrt{3})(z-\frac{\mathrm{i}}{\sqrt{3}})}\right]}_{z=-\frac{\mathrm{i}}{\sqrt{3}}}]\\ =& \frac{8\pi }{3}[\frac{\frac{\mathrm{i}}{\sqrt{3}}}{(\frac{\mathrm{i}}{\sqrt{3}}+\mathrm{i}\sqrt{3})(\frac{\mathrm{i}}{\sqrt{3}}-\mathrm{i}\sqrt{3})(\frac{\mathrm{i}}{\sqrt{3}}+\frac{\mathrm{i}}{\sqrt{3}})}+\frac{-\frac{\mathrm{i}}{\sqrt{3}}}{(-\frac{\mathrm{i}}{\sqrt{3}}+\mathrm{i}\sqrt{3})(-\frac{\mathrm{i}}{\sqrt{3}}-\mathrm{i}\sqrt{3})(-\frac{\mathrm{i}}{\sqrt{3}}-\frac{\mathrm{i}}{\sqrt{3}})}]\\ =& \frac{8\pi }{3}[\frac{\frac{\mathrm{i}}{\sqrt{3}}}{\left(\frac{4}{\sqrt{3}}\mathrm{i}\right)(-\frac{2}{\mathrm{i}\sqrt{3}})\left(\frac{2}{\mathrm{i}\sqrt{3}}\right)}+\frac{-\frac{\mathrm{i}}{\sqrt{3}}}{\left(\frac{2}{\sqrt{3}}\mathrm{i}\right)(-\frac{4}{\sqrt{3}}\mathrm{i})(-\frac{2}{\sqrt{3}}\mathrm{i})}]\\ =& \frac{8\pi }{3}[\frac{\frac{\mathrm{i}}{\sqrt{3}}}{\mathrm{i}\left(\frac{4}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)}+\frac{-\frac{\mathrm{i}}{\sqrt{3}}}{-\mathrm{i}\left(\frac{2}{\sqrt{3}}\right)\left(\frac{4}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)}]\\ =& \frac{8\pi }{3}[\frac{\frac{1}{\sqrt{3}}}{\left(\frac{4}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)}+\frac{\frac{1}{\sqrt{3}}}{\left(\frac{2}{\sqrt{3}}\right)\left(\frac{4}{\sqrt{3}}\right)\left(\frac{2}{\sqrt{3}}\right)}]\\ =& \frac{8\pi }{3}[\frac{\frac{1}{\sqrt{3}}}{\frac{16}{3\sqrt{3}}}+\frac{\frac{1}{\sqrt{3}}}{\frac{16}{3\sqrt{3}}}]\\ =& \frac{8\pi }{3}[\frac{3}{16}+\frac{3}{16}]\\ =& \pi .\end{array}$$

Exemple 3a – intégrales trigonométriques

La méthode décrite ici est utile pour les intégrales de la forme $$\underset{0}{\overset{2\pi }{\int }}\frac{P(\sin (t),\sin (2t),\dots ,\cos (t),\cos (2t),\dots )}{Q(\sin (t),\sin (2t),\dots ,\cos (t),\cos (2t),\dots )}\mathrm{d}t$$

où Modèle:Mvar et Modèle:Mvar sont des polynômes, i.e. une fonction rationnelle de termes trigonométrique est intégrée. On notera que les bornes d'intégration peuvent être Modèle:Math est Modèle:Math, comme dans l'exemple, ou les extrémités tout intervalle de longueur Modèle:Math.

L'astuce est d'utiliser la substitution Modèle:Math où Modèle:Math et donc $$\frac{1}{\mathrm{i}z}\mathrm{d}z=\mathrm{d}t.$$

Cette substitution envoie l'intervalle Modèle:Math sur le cercle unité. De plus, $$\sin (kt)=\frac{{\mathrm{e}}^{\mathrm{i}kt}-{\mathrm{e}}^{-\mathrm{i}kt}}{2\mathrm{i}}=\frac{z^k-z^{-k}}{2i}$$ et $$\cos (kt)=\frac{{\mathrm{e}}^{\mathrm{i}kt}+{\mathrm{e}}^{-\mathrm{i}kt}}{2}=\frac{z^k+z^{-k}}{2}$$ de sorte qu'une fonction rational Modèle:Math en Modèle:Mvar résulte de la substitution, est l'intégrale devient $${\oint }_{|z|=1}f(z)\frac{1}{\mathrm{i}z}\mathrm{d}z$$ qui à son tour se calcule en sommant les résidus de Modèle:Math dans le cercle unité.

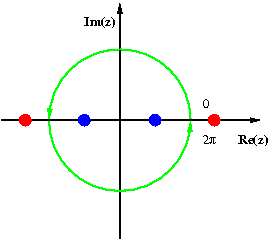
On prend par exemple l'intégrale $$I=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1}{1+(\sin t{)}^2}\mathrm{d}t.$$ On doit d'abord voir que $$I=\frac{1}{4}\underset{0}{\overset{2\pi }{\int }}\frac{1}{1+(\sin t{)}^2}\mathrm{d}t.$$

La substitution donne $$\frac{1}{4}{\oint }_{|z|=1}\frac{4\mathrm{i}z}{z^4-6z^2+1}\mathrm{d}z={\oint }_{|z|=1}\frac{\mathrm{i}z}{z^4-6z^2+1}\mathrm{d}z.$$

Les poles de cette fonction sont en Modèle:Math et Modèle:Math. De ces quatre poles, Modèle:Math et Modèle:Math sont hors du cercle unité (en rouge), mais Modèle:Math et Modèle:Math (en bleu) sont à l'intérieur. Les résidus correspondants sont tous deux égaux à Modèle:Math, ainsi l'intégrale vaut $$I=2\pi \mathrm{i}\times 2\times (-\frac{\sqrt{2}}{16}\mathrm{i})=\pi \frac{\sqrt{2}}{4}.$$

Exemple 4 – intégrales sur branches

On considère l'intégrale réelle $$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}\mathrm{d}x.$$

On peut d'abord commencer par poser l'intégrale de contour $$\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}\mathrm{d}z=I.$$

Si les résultats utilisés pour le calcul des résidus restent les mêmes, il faut noter que Modèle:Math, donc Modèle:Math a un point de branchement, ce qui doit être pris en compte dans le choix du contour Modèle:Mvar. Normalement le branchement du logarithme est définie comme le demi-axe réel négatif, cependant, ce choix rend le calcul de l'intégrale un peu compliqué, donc on choisira le demi-axe réel positif.

On utilise alors le contour du "trou de serrure", formé d'un petit cercle ouvert de rayon Modèle:Mvar, s'étendant sur un segment parallèle au demi-axe jusqu'à un autre cercle ouvert.

Notons que Modèle:Math et Modèle:Math sont dans le grand cercle. Ce sont les deux poles restants, dérivables en factorisant le dénominateur de l'intégrande. Le point de branchement en Modèle:Math est évité en le contournant. Modèle:Clear

Soit Modèle:Mvar le petit cercle de rayon Modèle:Mvar, Modèle:Math le plus grand, de rayon Modèle:Mvar, alors $$\underset{C}{\int }=\underset{\epsilon }{\overset{R}{\int }}+\underset{\mathrm{\Gamma }}{\int }+\underset{R}{\overset{\epsilon }{\int }}+\underset{\gamma }{\int }.$$

On peut voir que les intégrales sur Modèle:Math et Modèle:Mvar tendent toutes deux vers 0 pour Modèle:Math et Modèle:Math, par une estimation donnée au-dessus, ce qui laisse deux termes. Comme Modèle:Math, sur le contour hors du branchement, on a gagné Modèle:Math en argument le long de Modèle:Mvar. (Par l'identité d'Euler, Modèle:Math représente le vecteur unité, donc a un log égal à Modèle:Math, ce qui correspond à l'argument de Modèle:Mvar. Le coefficient de Modèle:Sfrac force à utiliser Modèle:Math.) Ainsi $$\begin{array}{cc}\underset{R}{\overset{\epsilon }{\int }}\frac{\sqrt{z}}{z^2+6z+8}\mathrm{d}z& =\underset{R}{\overset{\epsilon }{\int }}\frac{{\mathrm{e}}^{\frac{1}{2}\mathrm{Log}z}}{z^2+6z+8}\mathrm{d}z\\ & =\underset{R}{\overset{\epsilon }{\int }}\frac{{\mathrm{e}}^{\frac{1}{2}(\log |z|+\mathrm{i}\arg z)}}{z^2+6z+8}\mathrm{d}z\\ & =\underset{R}{\overset{\epsilon }{\int }}\frac{{\mathrm{e}}^{\frac{1}{2}\log |z|}{e}^{\frac{1}{2}(2\pi \mathrm{i})}}{z^2+6z+8}\mathrm{d}z\\ & =\underset{R}{\overset{\epsilon }{\int }}\frac{{\mathrm{e}}^{\frac{1}{2}\log |z|}{e}^{\pi \mathrm{i}}}{z^2+6z+8}\mathrm{d}z\\ & =\underset{R}{\overset{\epsilon }{\int }}\frac{-\sqrt{z}}{z^2+6z+8}\mathrm{d}z\\ & =\underset{\epsilon }{\overset{R}{\int }}\frac{\sqrt{z}}{z^2+6z+8}\mathrm{d}z.\end{array}$$

Ainsi : $$\underset{C}{\int }\frac{\sqrt{z}}{z^2+6z+8}\mathrm{d}z=2\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}\mathrm{d}x.$$

Avec le théorème des résidus ou la formule intégrale de Cauchy (d'abord en la méthode des fractions partielles pour dériver une somme de deux intégrales de contour simples) on obtient $$\pi \mathrm{i}(\frac{\mathrm{i}}{\sqrt{2}}-\mathrm{i})=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\sqrt{x}}{x^2+6x+8}\mathrm{d}x=\pi (1-\frac{1}{\sqrt{2}}).◻$$

Exemple 5 – le carré du logarithme

Cette section traite des intégrales semblables à l'exemple suivant : $$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\log x}{{(1+x^2)}^2}\mathrm{d}x.$$

Pour le calcul des intégrales, on utilise la fonction $$f(z)={\left(\frac{\log z}{1+z^2}\right)}^2$$ et la branche du logarithme correspond à Modèle:Math.

On va calculer l'intégrale de Modèle:Math le long du contour "trou de serrure" décrit en image. Comme il s'avère que cette intégrale est un multiple de l'intégrale initiale et par le théorème des résidus, on a $$\begin{array}{cc}(\underset{R}{\int }+\underset{M}{\int }+\underset{N}{\int }+\underset{r}{\int })f(z)\mathrm{d}z& =2\pi \mathrm{i}({\mathrm{Res}}_{z=i}f(z)+{\mathrm{Res}}_{z=-i}f(z))\\ & =2\pi \mathrm{i}(-\frac{\pi }{4}+\frac{1}{16}\mathrm{i}{\pi }^2-\frac{\pi }{4}-\frac{1}{16}\mathrm{i}{\pi }^2)\\ & =-\mathrm{i}{\pi }^2.\end{array}$$

Soit Modèle:Mvar le rayon du grand cercle, et Modèle:Mvar le rayon du petit. On note le segment supérieur Modèle:Mvar, et Modèle:Mvar le segment inférieur. Comme auparavant, on prend la limite en Modèle:Math et Modèle:Math. Les contributions sur les deux cercles tendent à s'annuler. Par exemple, on peut majorer, par le lemme d'estimation avec : $$|\underset{R}{\int }f(z)\mathrm{d}z|\le 2\pi R\frac{(\log R{)}^2+{\pi }^2}{{(R^2-1)}^2}\to 0.$$

Afin de calculer les contributions de Modèle:Mvar et Modèle:Mvar on pose Modèle:Math sur Modèle:Mvar et Modèle:Math sur Modèle:Mvar, avec Modèle:Math: $$\begin{array}{cc}-\mathrm{i}{\pi }^2& =(\underset{R}{\int }+\underset{M}{\int }+\underset{N}{\int }+\underset{r}{\int })f(z)\mathrm{d}z\\ & =(\underset{M}{\int }+\underset{N}{\int })f(z)\mathrm{d}z& & \underset{R}{\int },\underset{r}{\int }\to 0\\ & =-\underset{\mathrm{\infty }}{\overset{0}{\int }}{\left(\frac{\log (-x+\mathrm{i}\epsilon )}{1+(-x+\mathrm{i}\epsilon {)}^2}\right)}^2\mathrm{d}x-\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{\log (-x-\mathrm{i}\epsilon )}{1+(-x-i\epsilon {)}^2}\right)}^2\mathrm{d}x\\ & =\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{\log (-x+\mathrm{i}\epsilon )}{1+(-x+\mathrm{i}\epsilon {)}^2}\right)}^2\mathrm{d}x-\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{\log (-x-\mathrm{i}\epsilon )}{1+(-x-i\epsilon {)}^2}\right)}^2\mathrm{d}x\\ & =\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{\log x+\mathrm{i}\pi }{1+x^2}\right)}^2\mathrm{d}x-\underset{0}{\overset{\mathrm{\infty }}{\int }}{\left(\frac{\log x-\mathrm{i}\pi }{1+x^2}\right)}^2\mathrm{d}x& & \epsilon \to 0\\ & =\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{(\log x+\mathrm{i}\pi {)}^2-(\log x-\mathrm{i}\pi {)}^2}{{(1+x^2)}^2}\mathrm{d}x\\ & =\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{4\pi \mathrm{i}\log x}{{(1+x^2)}^2}\mathrm{d}x\\ & =4\pi \mathrm{i}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\log x}{{(1+x^2)}^2}\mathrm{d}x\end{array}$$

ce qui donne $$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{\log x}{{(1+x^2)}^2}\mathrm{d}x=-\frac{\pi }{4}.$$

Exemple 6 – logarithmes et le résidu à l'infini

On veut évaluer $$I=\underset{0}{\overset{3}{\int }}\frac{x^{\frac{3}{4}}(3-x{)}^{\frac{1}{4}}}{5-x}\mathrm{d}x.$$ ce qui implique de considérer $$f(z)=z^{\frac{3}{4}}(3-z{)}^{\frac{1}{4}}.$$

On construit Modèle:Math telle qu'il y ait un branchement sur [0, 3], en rouge dans le schéma. Pour ce faire, on choisit deux branchements du logarithme, ce qui donne $$z^{\frac{3}{4}}=\exp (\frac{3}{4}\log z)\text{avec}-\pi \le \arg z<\pi$$ et $$(3-z{)}^{\frac{1}{4}}=\exp (\frac{1}{4}\log (3-z))\text{avec}0\le \arg (3-z)<2\pi .$$

Le branchement de Modèle:Math est donc ]−∞, 0] et le branchement de Modèle:Math est ]−∞, 3]. Il est simple de voir que le branchement du produit des deux, i.e. Modèle:Math, est Modèle:Math, car Modèle:Math est en fait continue sur ]−∞, 0[. Ceci apparait pour Modèle:Math et quand on approche le branchement par au-dessus, Modèle:Math a la valeur $$r^{\frac{3}{4}}{\mathrm{e}}^{\frac{3}{4}\mathrm{i}\pi }(3+r{)}^{\frac{1}{4}}{\mathrm{e}}^{\frac{2}{4}\mathrm{i}\pi }=r^{\frac{3}{4}}(3+r{)}^{\frac{1}{4}}{\mathrm{e}}^{\frac{5}{4}\mathrm{i}\pi }.$$

En l'approchant par en-dessous, Modèle:Math a la valeur $$r^{\frac{3}{4}}{\mathrm{e}}^{-\frac{3}{4}\mathrm{i}\pi }(3+r{)}^{\frac{1}{4}}{\mathrm{e}}^{\frac{0}{4}\mathrm{i}\pi }=r^{\frac{3}{4}}(3+r{)}^{\frac{1}{4}}{\mathrm{e}}^{-\frac{3}{4}\mathrm{i}\pi }.$$

Mais $${\mathrm{e}}^{-\frac{3}{4}\mathrm{i}\pi }={\mathrm{e}}^{\frac{5}{4}\mathrm{i}\pi },$$ donc il y a continuité à travers le branchement. C'est illustré dans le schéma, où les deux cercles noirs orientés sont notés avec la valeur correspondante de l'argument du logarithme dans Modèle:Math et Modèle:Math.

On utilise le contour en vert dans le schéma. Pour faire cela, on doit calculer la valeur de Modèle:Math le long des segments juste au-dessus et en-dessous du branchement.

Soit Modèle:Math (à la limite, i.e. quand les deux cercles verts se réduisent vers un point), où Modèle:Math. Le long du segment d'au-dessus, on trouve que Modèle:Math a la valeur $$r^{\frac{3}{4}}{\mathrm{e}}^{\frac{0}{4}\mathrm{i}\pi }(3-r{)}^{\frac{1}{4}}{\mathrm{e}}^{\frac{2}{4}\mathrm{i}\pi }=\mathrm{i}{r}^{\frac{3}{4}}(3-r{)}^{\frac{1}{4}}$$ et le long du segment d'en-dessous, $$r^{\frac{3}{4}}{\mathrm{e}}^{\frac{0}{4}\mathrm{i}\pi }(3-r{)}^{\frac{1}{4}}{\mathrm{e}}^{\frac{0}{4}\mathrm{i}\pi }=r^{\frac{3}{4}}(3-r{)}^{\frac{1}{4}}.$$

Il suit que l'intégrale de Modèle:Math le long du segment vaut Modèle:Math à la limite, et le long du segment d'en-dessous, Modèle:Mvar.

Si on peut montrer que les intégrale sur les deux cercles s'annulent à la limite, alors on a également la valeur de Modèle:Math, par le théorème des résidus. On note Modèle:Mvar le rayon des cercles verts, avec Modèle:Math et Modèle:Math, pour appliquer le lemme d'estimation. Pour le cercle de gauche Modèle:Math on obtient $$\left|\underset{C_{\mathrm{L}}}{\int }\frac{f(z)}{5-z}\mathrm{d}z\right|\le 2\pi \rho \frac{{\rho }^{\frac{3}{4}}3.001^{\frac{1}{4}}}{4.999}\in 𝒪\left({\rho }^{\frac{7}{4}}\right)\to 0.$$

De même, sur le cercle à droite Modèle:Math, on a $$\left|\underset{C_{\mathrm{R}}}{\int }\frac{f(z)}{5-z}\mathrm{d}z\right|\le 2\pi \rho \frac{3.001^{\frac{3}{4}}{\rho }^{\frac{1}{4}}}{1.999}\in 𝒪\left({\rho }^{\frac{5}{4}}\right)\to 0.$$

Avec le théorème des résidus, on a $$(-\mathrm{i}+1)I=-2\mathrm{i}\pi ({\mathrm{Res}}_{z=5}\frac{f(z)}{5-z}+{\mathrm{Res}}_{z=\mathrm{\infty }}\frac{f(z)}{5-z}).$$ où le signe moins vient que le chemin autour des résidus est parcouru dans le sens horaire. En utilisant la branche du logarithme défini plus tôt, on trouve $${\mathrm{Res}}_{z=5}\frac{f(z)}{5-z}=-5^{\frac{3}{4}}{\mathrm{e}}^{\frac{1}{4}\log (-2)}.$$

Le pole est montré en bleu sur le schéma. La valeur se simplifie en $$-5^{\frac{3}{4}}{\mathrm{e}}^{\frac{1}{4}(\log 2+\mathrm{i}\pi )}=-{\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }{5}^{\frac{3}{4}}{2}^{\frac{1}{4}}.$$

On utilise la formule suivante pour les résidus à l'infini : $${\mathrm{Res}}_{z=\mathrm{\infty }}h(z)={\mathrm{Res}}_{z=0}(-\frac{1}{z^2}h\left(\frac{1}{z}\right)).$$

Par substitution, on trouve $$\frac{1}{5-\frac{1}{z}}=-z(1+5z+5^2{z}^2+5^3{z}^3+\cdots )$$ et $${\left(\frac{1}{z^3}(3-\frac{1}{z})\right)}^{\frac{1}{4}}=\frac{1}{z}(3z-1{)}^{\frac{1}{4}}=\frac{1}{z}{\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }(1-3z{)}^{\frac{1}{4}},$$ en utilisant l'égalité Modèle:Math sur la deuxième branche du logarithme. Ensuite, on applique le développement binomial, qui donne $$\frac{1}{z}{\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }(1-(\genfrac{}{}{0ex}{}{1/4}{1})3z+(\genfrac{}{}{0ex}{}{1/4}{2})3^2{z}^2-(\genfrac{}{}{0ex}{}{1/4}{3})3^3{z}^3+\cdots ).$$

On en conclut $${\mathrm{Res}}_{z=\mathrm{\infty }}\frac{f(z)}{5-z}={\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }(5-\frac{3}{4})={\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }\frac{17}{4}.$$

Enfin, il suit que la valeur de Modèle:Mvar est de $$I=2\pi \mathrm{i}\frac{{\mathrm{e}}^{\frac{1}{4}\mathrm{i}\pi }}{-1+\mathrm{i}}(\frac{17}{4}-5^{\frac{3}{4}}{2}^{\frac{1}{4}})=2\pi 2^{-\frac{1}{2}}(\frac{17}{4}-5^{\frac{3}{4}}{2}^{\frac{1}{4}})$$ dont on tire $$I=\frac{\pi }{2\sqrt{2}}(17-5^{\frac{3}{4}}{2}^{\frac{9}{4}})=\frac{\pi }{2\sqrt{2}}(17-40^{\frac{3}{4}}).$$

Évaluation par le théorème des résidus

Par le théorème des résidus, on peut évaluer des intégrales sur un contour fermé. On donne ici des exemples d'évaluation d'intégrales de contour par ce résultat.

Un premier exemple étudié sera $${\oint }_C\frac{{\mathrm{e}}^z}{z^3}\mathrm{d}z$$

On rappelle que le théorème dit que $${\oint }_{C}f(z)=2\pi \mathrm{i}\cdot \sum \mathrm{Res}(f,a_k),$$

avec Modèle:Math désignant le résidu de Modèle:Math.

Ici, Modèle:Math a un unique pole en 0. De là, on peut déterminer le résidu de Modèle:Math qui vaut Modèle:Sfrac. $$\begin{array}{cc}{\oint }_{C}f(z)& ={\oint }_C\frac{{\mathrm{e}}^z}{z^3}\\ & =2\pi \mathrm{i}\cdot {\mathrm{Res}}_{z=0}f(z)\\ & =2\pi \mathrm{i}{\mathrm{Res}}_{z=0}\frac{{\mathrm{e}}^z}{z^3}\\ & =2\pi \mathrm{i}\cdot \frac{1}{2}\\ & =\pi \mathrm{i}\end{array}$$

Le théorème des résidus permet de conclure : $${\oint }_C\frac{{\mathrm{e}}^z}{z^3}\mathrm{d}z=\pi \mathrm{i}.$$

Intégrales de contour multivariées

Pour calculer des intégrales de contour multivariées (i.e. des intégrales de surface, des intégrales de volume complexes ou des intégrales d'ordre élevé), on doit utiliser le théorème de la divergence. On supposera d'abord qu'on peut permuter Modèle:Math avec Modèle:Math, qui apparaissent dans la divergence du champ de vecteurs noté Modèle:Math. Ce théorème dit : $$\underset{n}{\underbrace{\int \cdots \underset{U}{\int }}}\mathrm{div}(𝐅)\mathrm{d}V=\underset{n-1}{\underbrace{\oint \cdots {\oint }_{\partial U}}}𝐅\cdot 𝐧\mathrm{d}S$$

De plus, on doit aussi évaluer Modèle:Math, qui est une notation alternative de Modèle:Math. La divergence de toute dimension peut être décrite comme $$\begin{array}{cc}\mathrm{div}(𝐅)& =\mathrm{\nabla }\cdot 𝐅\\ & =(\frac{\partial }{\partial u},\frac{\partial }{\partial x},\frac{\partial }{\partial y},\frac{\partial }{\partial z},\dots )\cdot (F_u,F_x,F_y,F_z,\dots )\\ & =(\frac{\partial F_u}{\partial u}+\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z}+\cdots )\end{array}$$

Exemple 1

Soit le champ de vecteurs Modèle:Math, dans le pavé $$0\le x\le 1,0\le y\le 3,-1\le z\le 4$$

L'intégrale de contour double correspondante sera définie comme: $$\int \subset \supset \underset{S}{\int }𝐅\cdot 𝐧\mathrm{d}S$$

On évalue maintenant Modèle:Math, par l'intégrale triple correspondante : $$\begin{array}{cc}\int \subset \supset \underset{S}{\int }𝐅\cdot 𝐧\mathrm{d}S& =\int \int \underset{V}{\int }(\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z})\mathrm{d}V\\ & =\int \int \underset{V}{\int }(\frac{\partial \sin (2x)}{\partial x}+\frac{\partial \sin (2y)}{\partial y}+\frac{\partial \sin (2z)}{\partial z})\mathrm{d}V\\ & =\int \int \underset{V}{\int }2(\cos (2x)+\cos (2y)+\cos (2z))\mathrm{d}V\\ & =\underset{0}{\overset{1}{\int }}\underset{0}{\overset{3}{\int }}\underset{-1}{\overset{4}{\int }}2(\cos (2x)+\cos (2y)+\cos (2z))\mathrm{d}x\mathrm{d}y\mathrm{d}z\\ & =\underset{0}{\overset{1}{\int }}\underset{0}{\overset{3}{\int }}(10\cos (2y)+\sin (8)+\sin (2)+10\cos (z))\mathrm{d}y\mathrm{d}z\\ & =\underset{0}{\overset{1}{\int }}(30\cos (2z)+3\sin (2)+3\sin (8)+5\sin (6))\mathrm{d}z\\ & =18\sin (2)+3\sin (8)+5\sin (6)\end{array}$$

Exemple 2

On considère le champ de vecteurs Modèle:Math, et Modèle:Mvar désigne la quatrième dimension. On borne ce champ de vecteurs par le pavé : $$0\le x\le 1,-10\le y\le 2\pi ,4\le z\le 5,-1\le u\le 3$$

On utilise donc le théorème de la divergence. Un élément de volume est donc Modèle:Math. $$\begin{array}{cc}\int \subset \int \supset \underset{S}{\int }𝐅\cdot 𝐧\mathrm{d}S& =\underset{V}{⨌}(\frac{\partial F_u}{\partial u}+\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}+\frac{\partial F_z}{\partial z})\mathrm{d}V\\ & =\underset{V}{⨌}(\frac{\partial u^4}{\partial u}+\frac{\partial x^5}{\partial x}+\frac{\partial y^6}{\partial y}+\frac{\partial z^{-3}}{\partial z})\mathrm{d}V\\ & =\underset{V}{⨌}\frac{4u^3{z}^4+5x^4{z}^4+5y^4{z}^4-3}{z^4}\mathrm{d}V\\ & =\underset{V}{⨌}\frac{4u^3{z}^4+5x^4{z}^4+5y^4{z}^4-3}{z^4}\mathrm{d}V\\ & =\underset{0}{\overset{1}{\int }}\underset{-10}{\overset{2\pi }{\int }}\underset{4}{\overset{5}{\int }}\underset{-1}{\overset{3}{\int }}\frac{4u^3{z}^4+5x^4{z}^4+5y^4{z}^4-3}{z^4}\mathrm{d}V\\ & =\underset{0}{\overset{1}{\int }}\underset{-10}{\overset{2\pi }{\int }}\underset{4}{\overset{5}{\int }}\left(\frac{4(3u^4{z}^3+3y^6+91z^3+3)}{3z^3}\right)\mathrm{d}y\mathrm{d}z\mathrm{d}u\\ & =\underset{0}{\overset{1}{\int }}\underset{-10}{\overset{2\pi }{\int }}(4u^4+\frac{743440}{21}+\frac{4}{z^3})\mathrm{d}z\mathrm{d}u\\ & =\underset{0}{\overset{1}{\int }}(-\frac{1}{2{\pi }^2}+\frac{1486880\pi }{21}+8\pi u^4+40u^4+\frac{371720021}{1050})\mathrm{d}u\\ & =\frac{371728421}{1050}+\frac{14869136{\pi }^3-105}{210{\pi }^2}\\ & \approx 576468,77\end{array}$$

On peut ainsi évaluer une intégrale de contour de la quatrième dimension.

Représentation intégrale

Modèle:... Une représentation intégrale de fonction est une expression de la fonction impliquée dans une intégrale de contour. Plusieurs représentations intégrales sont connus pour de nombreuses fonctions spéciales. Les représentations intégrales peuvent être importantes pour des raisons théoriques, e.g. obtenir des prolongements analytiques ou des équations fonctionnelles, ou parfois des évaluations numériques.

Le contour de Hankel

Par exemple, la définition originale de la fonction zêta de Riemann Modèle:Math par une série de Dirichlet, $$\zeta (s)=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n^s},$$ est valide seulement pour Modèle:Math. Mais $$\zeta (s)=-\frac{\mathrm{\Gamma }(1-s)}{2\pi \mathrm{i}}\underset{H}{\int }\frac{(-t{)}^{s-1}}{{\mathrm{e}}^t-1}\mathrm{d}t,$$

où l'intégration est faite sur le contour de Hankel Modèle:Mvar, et est valide pour tout complexe Modèle:Mvar différent de 1.

Voir aussi

• Résidu (analyse complexe)
• Valeur principale de Cauchy
• Intégrale de Poisson

Liens externes

• Modèle:Ouvrage
• Jean Jacquelin, Marko Riedel, Branche univalenteModèle:Lien brisé, Les-Mathematiques.net.
• Marko Riedel et al., Problème d'intégrale, Les-Mathematiques.net.
• Marko Riedel et al., Integral by residue, math.stackexchange.com.
• W W L Chen, Introduction to Complex Analysis
• Modèle:Es Auteurs multiples, sin límites ni cotas, es.ciencia.matematicas.

• Modèle:Springer