Fonction somme des diviseurs

Modèle:Redirect En arithmétique, la fonction somme des diviseurs est la fonction arithmétique qui, à un entier naturel non nul, associe la somme de ses diviseurs positifs, souvent notée Modèle:Math.

Ainsi Modèle:Math(6) = 1 + 2 + 3 + 6 = 12, Modèle:Math(p) = p + 1 pour tout nombre premier Modèle:Mvar et Modèle:Math(1) = 1.

Cette fonction intervient dans l'étude des nombres parfaits, amiables, déficients ou abondants, des nombres intouchables ou sublimes, ou dans les suites aliquotes. Elle est aussi étudiée dans le cadre de l'hypothèse de Riemann.

C'est un exemple de fonction multiplicative.

On étudie aussi parfois la somme s(Modèle:Mvar) = Modèle:Math(Modèle:Mvar) – Modèle:Mvar des diviseurs stricts d'un entier Modèle:Mvar, c'est-à-dire de tous les diviseurs positifs de Modèle:Mvar strictement inférieurs à Modèle:Mvar.

Propriétés

• Comme toutes les fonctions somme des puissances k-ième des diviseurs Modèle:Math, la fonction Modèle:Math est multiplicative, c'est-à-dire que, pour tous entiers Modèle:Mvar et Modèle:Mvar premiers entre eux, Modèle:Math(mn) = Modèle:Math(m)Modèle:Math(n).
• La somme des termes d'une suite géométrique permet de calculer la somme des diviseurs d'une puissance d'un nombre premier :Modèle:Retrait(La fonction Modèle:Math n'est donc pas complètement multiplicative.)
• L'utilisation des deux propriétés précédentes permet de déterminer la somme des diviseurs de Modèle:Math connaissant sa décomposition en facteurs premiers :Modèle:Centrer
• Au sens de la convolution de Dirichlet, on peut écrire $\sigma =\mathrm{I}\mathrm{d}\mathrm{*}\mathrm{𝟏}$. σ possède alors un inverse ${\sigma }^{-1}={\mathrm{𝟏}}^{-1}*\mathrm{I}{\mathrm{d}}^{\mathrm{-}\mathrm{1}}\mathrm{=}\mathrm{\mu }\mathrm{*}\mathrm{(}\mathrm{\mu }\mathrm{I}\mathrm{d}\mathrm{)}$, qu'on peut calculer explicitement : ${\sigma }^{-1}(n)$ est nul dès que $n$ admet un facteur cubique, et sinon en écrivant $n=(p_1{p}_2...p_r)(q_1{q}_2...q_l{)}^2$ où les $p_i$ et les $q_i$ sont des nombres premiers deux à deux distincts, on a ${\sigma }^{-1}(n)=(-1{)}^r(p_1+1)(p_2+1)...(p_r+1)q_1{q}_2...q_l$.
• On a l'identité  : $\sum _{k=1}^n\sigma (k)=\frac{1}{2}\sum _{d=1}^n\lfloor \frac{n}{d}\rfloor (\lfloor \frac{n}{d}\rfloor +1)$ où $\lfloor \cdot \rfloor$ désigne la fonction partie entière :

$\sum _{k=1}^n\sigma (k)=\sum _{k=1}^n\sum _{m|k}m=\sum _{\begin{array}{c}m,d\\ 1⩽md⩽n\end{array}}m=\sum _{d=1}^n\sum _{m=1}^{\lfloor \frac{n}{d}\rfloor }m=\frac{1}{2}\sum _{d=1}^n\lfloor \frac{n}{d}\rfloor (\lfloor \frac{n}{d}\rfloor +1).$

Loi d'Euler

Leonhard Euler énonce en 1752 un résultat, qu'il appelle Modèle:Citation, permettant de déterminer la somme des diviseurs de n à l'aide d'une formule de récurrence :

$\sigma (n)=\sigma (n-1)+\sigma (n-2)-\sigma (n-5)-\sigma (n-7)+\sigma (n-12)+\cdots$

où 1, 2, 5, 7, 12... est la suite des nombres pentagonaux généralisés (Modèle:OEIS). Modèle:Centrer avec Modèle:Retrait Par exemple, $\sigma (10)=\sigma (9)+\sigma (8)-\sigma (5)-\sigma (3)=13+15-6-4=18$.

Cette relation de récurrence est identique à celle vérifiée par la fonction Modèle:Mvar qui donne le nombre de partitions d'un entier, au détail près qu'on remplace la valeur $p(0)=1$ par la valeur $f_n(0)=n$.

Euler démontre cette loi en 1754 à l'aide de l'écriture en série d'un produit infini : Modèle:Retrait

Comportement asymptotique

En rouge, représentation de $\frac{\sum _{k=1}^n\sigma (k)}{n}$ ; en bleu, de $\frac{n}{2}{Q}_n-\frac{1}{2}{H}_n$ et $\frac{n}{2}{Q}_n+\frac{1}{2}{H}_n$ ; et en vert, de $\frac{{\pi }^2}{12}n$.

Moyenne de Cesàro

En moyenne de Cesàro, on a $\frac{\sum _{k=1}^n\sigma (k)}{n}=\frac{{\pi }^2}{12}n+O(\ln n)$. Ici et plus bas, O, o et Modèle:Math, sont les symboles de Landau.

Ceci vient de la formule $\sum _{k=1}^n\sigma (k)=\frac{1}{2}\sum _{k=1}^n({\lfloor \frac{n}{k}\rfloor }^2+\lfloor \frac{n}{k}\rfloor )$ Modèle:Supra, dont on déduit : $\frac{n}{2}{Q}_n-\frac{1}{2}{H}_n⩽\frac{\sum _{k=1}^n\sigma (k)}{n}⩽\frac{n}{2}{Q}_n+\frac{1}{2}{H}_n$ où

$Q_n=\sum _{k=1}^n\frac{1}{k^2}\to \frac{{\pi }^2}{6}$ (cf. Problème de Bâle) et $H_n=\sum _{k=1}^n\frac{1}{k}\sim \ln n$ (cf. Série harmonique).

En rouge, représentation de $\sigma (n)$ ; en bleu, de $\frac{{\pi }^2}{6}n$ ; en vert, le minorant $n+1$ correspondant aux nombres premiers ; et en cyan le majorant de Lagarias $H_n+\exp (H_n)\ln (H_n)$.

Ordre moyen

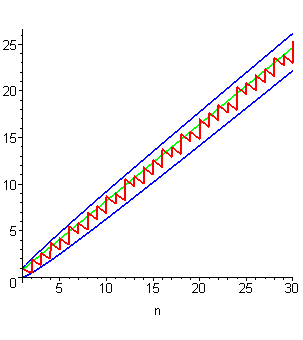
Un ordre moyen simple pour Modèle:Math(n) est $\frac{{\pi }^2}{6}n$, puisqu'on a Modèle:Supra l'estimation Modèle:Centrer où le terme E(x) est un o(x²).

Une bonne estimation de ce terme E(x) fournit une évaluation fine de la précision obtenue si l'on attribue à Modèle:Math(n) l'ordre moyen nπ²/6. Les meilleures majoration et minoration connues de cette précision sont données respectivement par Modèle:Centrer et par Modèle:Centrer Modèle:Clr

Somme des diviseurs et hypothèse de Riemann

La fonction somme des diviseurs a été étudiée dans le contexte de l'hypothèse de Riemann.

T. H. Gronwall a démontré en 1913 que Modèle:Retrait où Modèle:Math est la constante d'Euler-Mascheroni.

Le critère de Robin (du mathématicien français Guy Robin, en 1984) stipule que l'hypothèse de Riemann est vraie si et seulement si

$\sigma (n)<n{\mathrm{e}}^{\gamma }\ln (\ln (n))$

pour tout Modèle:Math ≥ 5 041.

Cette inégalité a déjà été établie pour 70,26 % des entiers naturels. (Les auteurs montrent que les entiers quadratfrei, de densité Modèle:Math, ainsi que les impairs, de densité 1/2, satisfont l'inégalité. Les impairs non quadratfrei étant de densité Modèle:Math, les entiers satisfaisant l'inégalité sont de densité au moins Modèle:Math .)

En 2001, Jeffrey Lagarias, en utilisant le critère de Robin, lie la somme des diviseurs au n-ième nombre harmonique HModèle:Ind et prouve que l'hypothèse de Riemann est vraie si et seulement si pour tout entier n, Modèle:Retrait

Autres expressions

La somme des diviseurs peut être exprimée sous forme de somme trigonométrique :

$\sigma (n)=\sum _{k=1}^n\sum _{j=1}^k\cos \frac{2\pi jn}{k}$.

Voir aussi

Articles connexes

• Ordre moyen d'une fonction arithmétique
• Théorème des nombres pentagonaux