Pavage de la sphère

Modèle:Voir homonymes Modèle:Images Un pavage de la sphère est un ensemble de portions de la surface d'une sphère dont l'union est la sphère entière, sans recouvrement. En pratique on s'intéresse surtout aux pavages réalisés avec des polygones sphériques (des portions de surface délimitées par des arcs de grand cercle), dénommés polyèdres sphériques.

Les pavages les plus connus sont le ballon de football, que l'on peut assimiler à un icosaèdre tronqué, et le ballon de plage, assimilable à un Modèle:Lien. Un autre pavage bien connu est celui délimité par des méridiens et des parallèles, mais il n'utilise pas que des arcs de grand cercle.

Coloriage

Une question apparemment anodine concerne le nombre de couleurs nécessaire au coloriage des différentes portions de surface (ou régions), de telle sorte que deux régions limitrophes (c'est-à-dire, ayant une frontière commune) ne reçoivent pas la même couleur. On sait depuis longtemps qu'en pratique il suffit de quatre couleurs, mais c'est une conjecture énoncée en 1852 qui n'a été démontrée qu'en 1976 (théorème des quatre couleurs).

Pavages générés par des polyèdres réguliers ou semi-réguliers

Pavage de la sphère par des triangles (icosaèdre déformé).

On peut paver la sphère en projetant depuis son centre n'importe quel polyèdre régulier ou semi-régulier (ou son dual) de même centre. Chacun de ces polyèdres sphériques peut être caractérisé par son symbole de Schläfli $\{p,q\}$ ou par sa figure de sommet $a.b.c\dots$.

Symbole de Schläfli	{p,q}	t{p,q}	r{p,q}	t{q,p}	{q,p}	rr{p,q}	tr{p,q}	sr{p,q}
Figure de sommet	pq	q.2p.2p	p.q.p.q	p. 2q.2q	qp	q.4.p. 4	4.2q.2p	3.3.q.3.p
Tétraédrique (3 3 2)	[[Tétraèdre|3Modèle:3]]	3.6.6	3.3.3.3	3.6.6	[[Tétraèdre|3Modèle:3]]	3.4.3.4	4.6.6	3.3.3.3.3
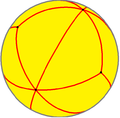		V3.6.6	V3.3.3.3	V3.6.6		V3.4.3.4	V4.6.6	V3.3.3.3.3
Octaédrique (4 3 2)	[[Cube|4Modèle:3]]	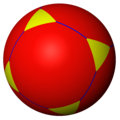3.8.8	3.4.3.4	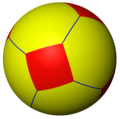4.6.6	[[Octaèdre|3Modèle:4]]	3.4.4.4	4.6.8	3.3.3.3.4
		V3.8.8	V3.4.3.4	V4.6.6		V3.4.4.4	V4.6.8	V3.3.3.3.4
Icosaédrique (5 3 2)	[[Dodécaèdre|5Modèle:3]]	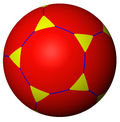3.10.10	3.5.3.5	5.6.6	[[Icosaèdre|3Modèle:5]]	3.4.5.4	4.6.10	3.3.3.3.5
		V3.10.10	V3.5.3.5	V5.6.6		V3.4.5.4	V4.6.10	V3.3.3.3.5
Diédrique Exemple Modèle:Nobr 6 (2 2 6)	Modèle:Lien	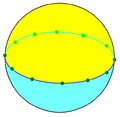Modèle:Lien	Modèle:Lien	6.4.4	Modèle:Lien	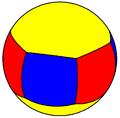4.6.4	4.4.12	3.3.3.6

Classe	2	3	4	5	6	7	8	10
Prisme (2 2 p)
Bipyramide (2 2 p)
Antiprisme
Trapézoèdre

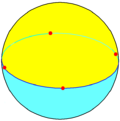
Cas dégénérés

On peut aussi paver la sphère par des polyèdres sphériques dégénérés, tels que les Modèle:Lien (symbole de Schläfli : $\{2,n\}$) et les Modèle:Lien réguliers ($\{n,2\}$).

Hosoèdres réguliers

Schläfli	{2,1}	{2,2}	{2,3}	{2,4}	{2,5}	{2,6}	{2,7}	{2,8}...
Coxeter	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD
Faces et arêtes	1	2	3	4	5	6	7	8
Sommets	2

Dièdres sphériques réguliers

Schläfli	h{2,2}={1,2}	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}...
Coxeter	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD	Modèle:DCD
Faces	2 {1}	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Arêtes et sommets	1	2	3	4	5	6

Correspondance avec le pavage du plan projectif

Les polyèdres sphériques ayant au moins une symétrie d'inversion sont liés aux Modèle:Lien, qui permettent le pavage du plan projectif.

Les polyèdres projectifs les mieux connus sont les polyèdres projectifs réguliers (quotients des solides de Platon à symétrie centrale), ainsi que deux classes infinies de Modèle:Lien pairs et d'Modèle:Lien :

• l'Modèle:Lien, {4,3}/2 ;
• l'Modèle:Lien, {3,4}/2 ;
• Modèle:Lien, {5,3}/2 ;
• l'Modèle:Lien, {3,5}/2 ;
• l'hémidièdre, {2p,2}/2, Modèle:Nobr ;
• l'hémihosoèdre, {2,2p}/2, Modèle:Nobr.

Pavage par des quadrilatères curvilignes

On peut paver la sphère par des quadrilatères curvilignes découpés par deux familles de courbes, notamment deux familles orthogonales (chaque courbe de la première famille coupe celles de la seconde à angle droit) ou plus généralement isogonales (l'angle d'intersection des courbes des deux familles est constant).

Le plus utilisé de ces pavages est celui formé par des méridiens et des parallèles, qu'on peut d'ailleurs appliquer à n'importe quelle surface de révolution (ellipsoïde, toreModèle:Etc.). En planétologie les quadrilatères du pavage sont dénommés quadrangles.

Quand un potentiel $V(\theta ,\phi )$ (où Modèle:Mvar et Modèle:Mvar sont la colatitude et la longitude) a été défini sur la sphère, les équipotentielles et les lignes de champ constituent deux familles orthogonales qui peuvent servir à paver la sphère.

Voir aussi

Articles connexes

• Géométrie sphérique
• Pavage d'une surface